4*. Теорема Бернуллі і стійкість відносних частот

Теорема. Нехай – число появ події в незалежних випробуваннях Бернуллі, – відносна частота цієї події, – імовірність появи події в одній спробі. Тоді для будь-якого

, (3)

тобто відносна частота події збігається за ймовірністю до її ймовірності .

Із твердження теореми Бернуллі випливає, що коли число випробувань є достатньо великим, то для будь-якого числа подія є практично вірогідною, тобто відносна частота події має властивість стійкості.

Зазначимо, що теорему Бернуллі можна розглядати як окремий випадок наведеного вище наслідку з теореми Чебишова, оскільки випадкова величина може бути представлена сумою незалежних однаково розподілених випадкових величин:

.

Це означає, що в теоремі Бернуллі йдеться про збіжність середнього арифметичного випадкових величин до математичного сподівання величини , тобто до ймовірності .

Зауважимо також, що в умовах теореми Бернуллі нерівність Чебишова, застосована до випадкової величини , має вигляд:

. (3')

Зауваження. На підставі теореми Бернуллі не слід робити висновок, що . Остання рівність означає, що для всіх , де – деяке велике натуральне число і – як завгодно мале число. А теорема Бернуллі тільки стверджує, що ймовірність є близькою до одиниці при досить великих , а нерівність для деяких навіть великих може не виконуватися.

Приклад 2. Використовуючи нерівність (3'), установити, яке число експериментів треба провести, щоб відхилення відносної частоти появ події від імовірності за абсолютною величиною було меншим за з імовірністю, не меншою за . Отриманий результат порівняти з оцінкою для , обчисленою за допомогою інтегральної формули Лапласа.

Розв’язання. За умовою задачі ; ; . Із нерівності (3') маємо:

,

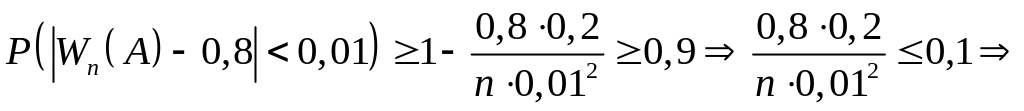
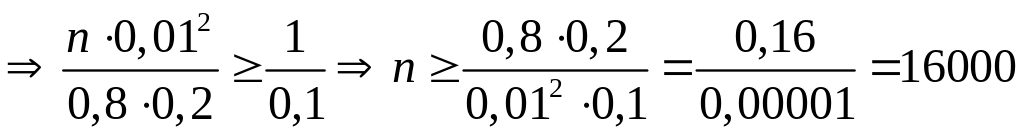тобто заданого відхилення відносної частоти події від її ймовірності буде досягнуто, якщо проведемо не менше ніж, випробувань.

Оцінки тепер ймовірність заданого відхилення за допомогою інтегральної теореми Лапласа. Одержимо:

.

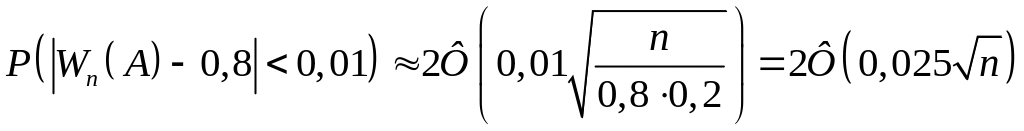За умовою задачі:

.

За таблицею значень інтегральної функції Лапласа знайдемо . Ураховуючи останню нерівність та беручи до уваги, що функція – монотонно зростаюча, маємо:

.

Звідси шукане число випробувань .

Отже, у даному випадку, як і в прикладі 1, застосування нерівності Чебишова дає грубу оцінку.

5*. Центральна гранична теорема

Ми розглянули теореми закону великих чисел, які встановлюють факт збіжності за ймовірністю послідовності деяких випадкових величин до сталих їх характеристик незалежно від їх закону розподілу. Група теорем, що стосуються граничних законів розподілу суми випадкових величин, об’єднані загальною назвою – центральна гранична теорема. Центральна гранична теорема встановлює умови, за яких указаний граничний закон є нормальним.

Наведемо одне з формулювань цієї теореми, доведеної О. М. Ляпуновим.

Центральна гранична теорема. Нехай – послідовність незалежних випадкових величин зі скінченними математичними сподіваннями і дисперсіями , .

Уведемо нові випадкові величини: 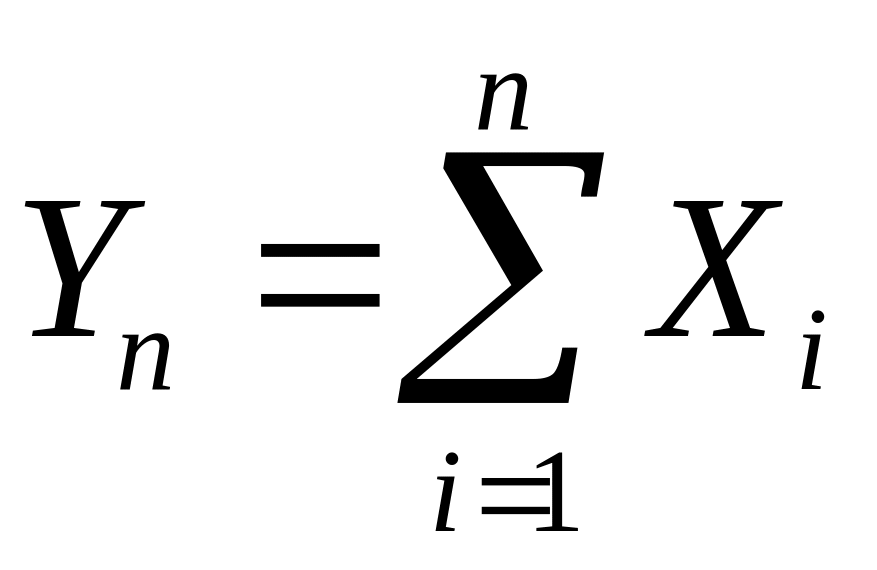, для яких , .

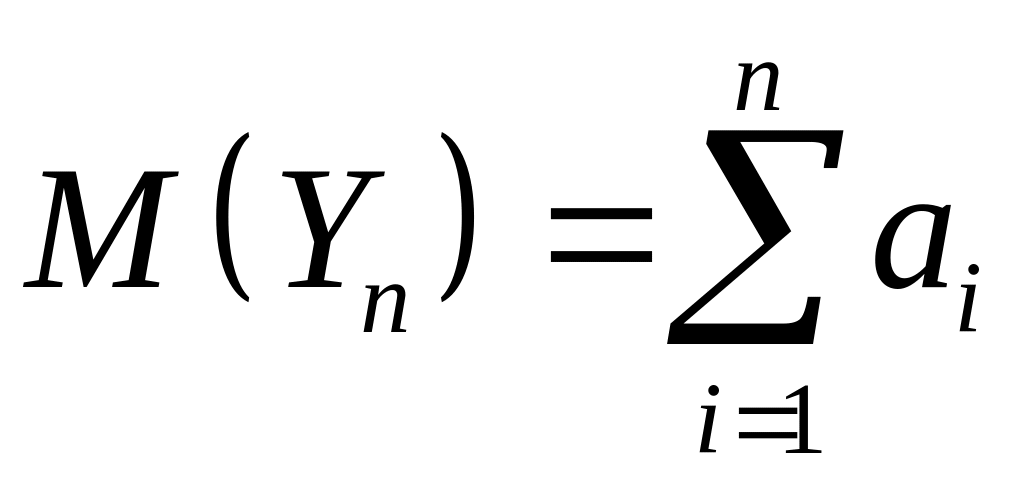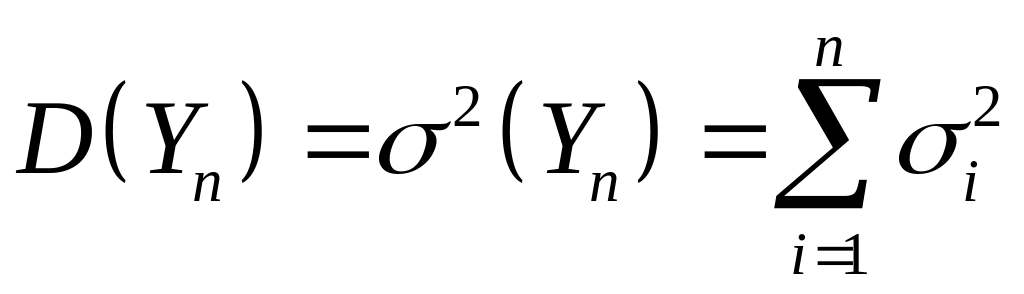Тоді, якщо виконана умова 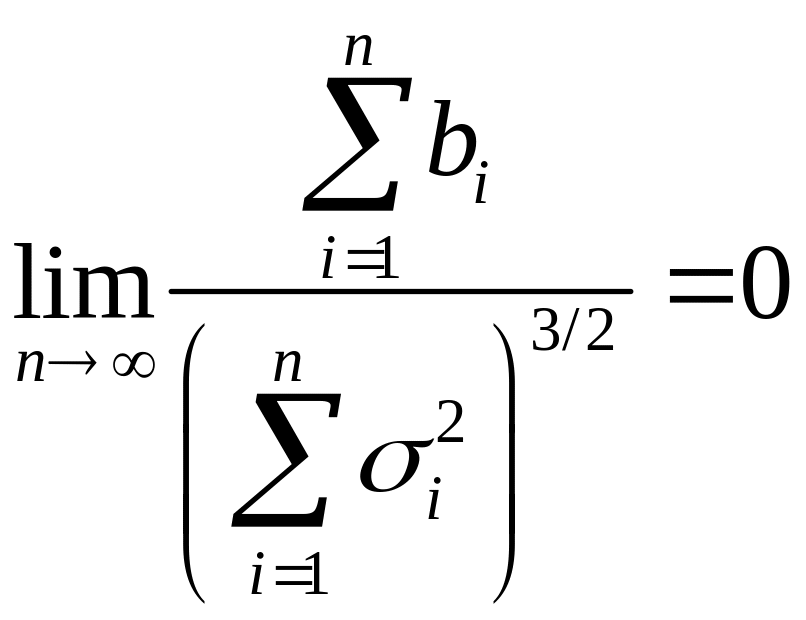, де , то для будь-якого числа виконується така гранична рівність:

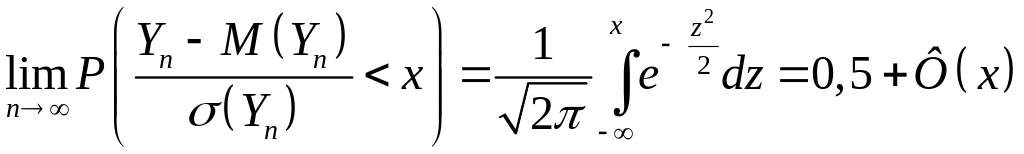. (4)

Рівність (4) означає, що закон розподілу нормованих відхилень суми за наближається до стандартного нормального закону розподілу. У цьому випадку кажуть, що має асимптотично-нормальний розподіл.

У подальших своїх дослідженнях О. М. Ляпунов довів справедливість граничного нормального розподілу за більш загальних умов: якщо існує таке число , для якого

,

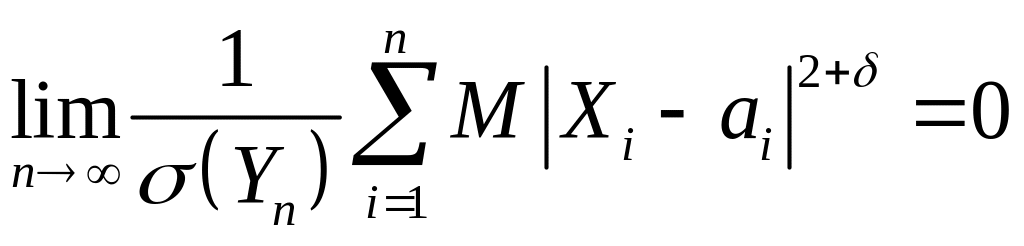то для будь-якого числа виконується гранична рівність (4).

Ця гранична рівність отримала назву умови Ляпунова.

На практиці центральна гранична теорема переважно використовується в тому разі, коли доданки мають однаковий розподіл. Наприклад, у математичній статистиці вибіркові випадкові величини мають однакові розподіли, оскільки ми їх отримуємо на базі однієї і тієї ж генеральної сукупності.

Наслідок із центральної граничної теореми. Нехай – послідовність незалежних однаково розподілених випадкових величин зі скінченними математичними сподіваннями , дисперсією і

, , .

Тоді для будь-якого

. (4')

Приклад 3. Кожна з незалежних випадкових величин , розподілена рівномірно на проміжку . Написати наближено густину і функцію розподілу випадкової величини

Розв’язання. Кожна зі випадкових величин має густину розподілу:

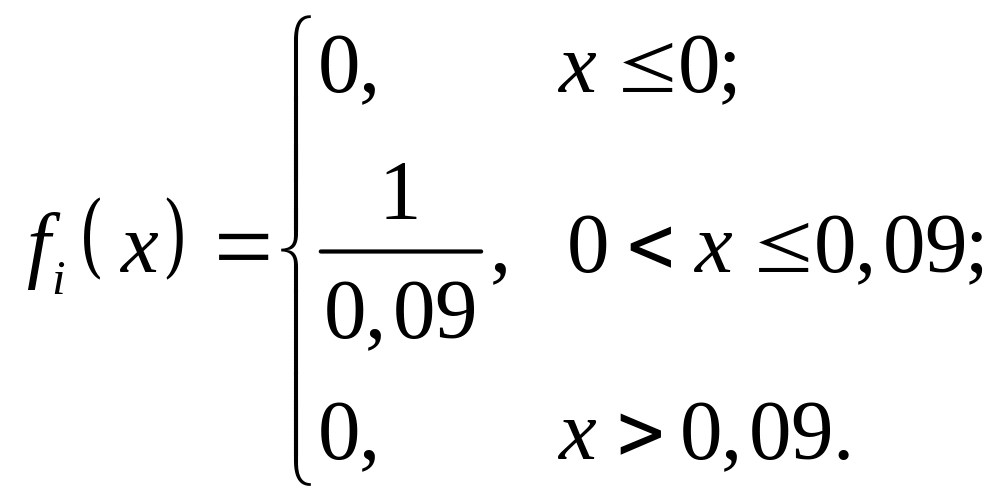
Обчислимо чисельні характеристики:

Оскільки для послідовності X), Х2,..., ХП9... виконані умови нас­лідку з центральної граничної теореми, то на підставі рівності (2.44') робимо висновок, що розподіл нормованої випадкової

У - 4 5 величини 2100 = 1?° ' можна наближено замінити на розпо-

/0,0675

діл стандартної нормальної випадкової величини 2 є N (0, 1) або, що те ж саме, розподіл випадкової величини У1Оо можна наближено замінити на нормальний розподіл із параметрами М густини розподілу / (х) та функції розподілу Р (х) випадкової величини Уюо будуть такі:

Приклад 2.24. У касі деякої установи залишилася сума А = 3500 грн. У черзі за одержанням грошей стоять 20 осіб. Сума X, яку потрібно ви­платити окремій особі, — випадкова величина з математичним споді­ванням М (X) = 150 грн. і середнім квадратичним відхиленням <т(Х) = 60 грн. Знайти ймовірність того, що суми й не вистачить для виплати грошей усім особам, які стоять у черзі.

Розв'язання. На підставі центральної граничної теореми для однаково розподілених доданків Х2- при великому п (а п = 20 практично можна вважати великим), випадкова величина

де X} — сума, яку потрібно виплатити йй особі, має приблиз­но нормальний розподіл із параметрами:

МЮ = п-М(Х); ОД) = п-Д*); а(Уп) = Гп-а(Х);

або

Отже, з імовірністю, близькою до , наявної в касі суми грошей не вистачить для виплати всім бажаючим особам.

9