2*. Нерівність Чебишова та збіжність за ймовірністю

Теоретичну основу закону великих чисел становлять нерівність Чебишева та поняття збіжності послідовності випадкових величин за ймовірністю.

Нерівність Чебишова. Якщо випадкова величина має скінченні математичне сподівання та дисперсію , то для будь-якого числа виконується нерівність:

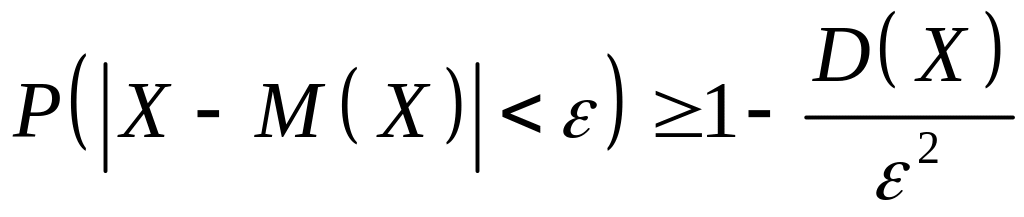, (1)

тобто ймовірність того, що відхилення значень випадкової величини від її математичного сподівання буде меншим за абсолютним значенням від додатного числа є не меншою, ніж .

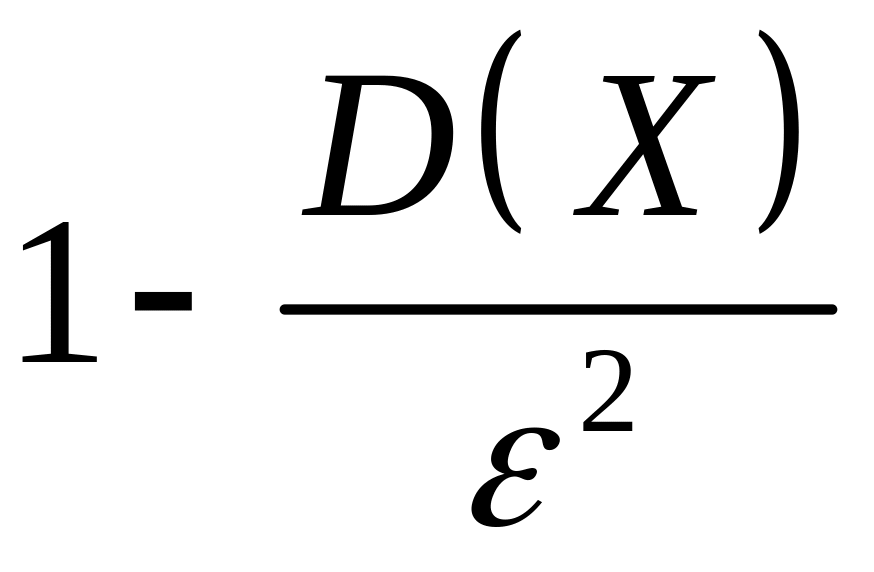Нерівність (1) називається нерівністю Чебишова і в разі малого числа вона дає оцінку знизу ймовірності того, що величина набуде значення, досить близького до її математичного сподівання .

Для оцінки ймовірності зверху використовують нерівність Маркова: якщо випадкова величина набуває тільки невід’ємних значень і , то для будь-якого виконується нерівність:

.

Приклад 1. Майстерня обслуговує телевізорів. Імовірність того, що кожний зі телевізорів витримає гарантійний термін роботи, становить . За допомогою нерівності Чебишова оцінити ймовірність випадкової події, яка полягає в тому, що більше ніж і менше ніж телевізорів витримають гарантійний термін роботи. Отриманий результат порівняти з імовірністю цієї ж події, обчисленої за допомогою інтегральної формули Лапласа.

Розв’язання. Нехай випадкова величина – число телевізорів, що витримають гарантійний термін роботи. Оскільки маємо незалежних експериментів, у кожному з яких імовірність появи події (один телевізор витримає гарантійний ремонт) , то

; .

(Див. формули для обчислення математичного сподівання і дисперсії числа появ події в послідовних випробуваннях за схемою Бернуллі). Маємо ланцюжок рівносильних нерівностей:

і за нерівністю Чебишова:

,

тобто ймовірність того, що від до телевізорів витримають гарантійний ремонт, є не меншою ніж .

Достатньо точне значення шуканої ймовірності одержимо, використовуючи асимптотичну інтегральну формулу Лапласа:

.

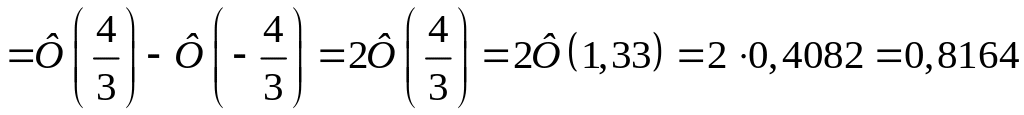Порівнюючи отримані результати для , робимо висновок, що в даному випадку нерівність Чебишова дає грубу оцінку. Це означає, що нерівність Чебишова для практики має обмежене значення. Проте теоретичне значення цієї нерівності є дуже велике. На базі нерівності Чебишова доводяться теореми закону великих чисел.

Збіжність послідовності випадкових величин за ймовірністю

Сформулюємо тепер математичне поняття збіжності послідовності випадкових величин за ймовірністю.

Нехай задана послідовність випадкових величин: .

Кажуть, що ця послідовність збігається за ймовірністю до невипадкової величини , якщо за необмеженого збільшення імовірність події (де – як завгодно мале фіксоване число) наближається до одиниці, тобто:

.

Іншими словами, якими б не були як завгодно малі наперед задані числа і , завжди можна знайти таке велике число , що для всіх номерів , більших за , виконується нерівність:

.

3*. Теорема Чебишова і стійкість середнього арифметичного випадкових величин

Теорема. Нехай випадкові величини попарно незалежні, мають скінченні математичні сподівання , та обмежені в сукупності дисперсії , . Позначимо:

, , .

Тоді для будь-якого числа

, (2)

тобто різниця між середнім арифметичним випадкових величин і середнім арифметичним їх математичних сподівань збігається за ймовірністю до нуля.

Суть теореми Чебишова полягає в тому, що хоч окремі випадкові величини можуть набувати значень, досить віддалених від своїх математичних сподівань , зате середнє арифметичне великого числа цих випадкових величин із імовірністю, близькою до одиниці, набуває значення, яке близьке до середнього арифметичного їх математичних сподівань. Тобто середнє арифметичне великого числа незалежних випадкових величин втрачає випадковий характер і має властивість стійкості.

Теорема Чебишова знаходить важливе практичне застосування. Зокрема, на цій теоремі ґрунтується вибірковий метод, який широко використовується в статистиці. Суть його полягає в тому, що на підставі вивчення певної ознаки для достатньо великої випадкової вибірки об’єктів роблять висновок про всю їх сукупність (генеральну сукупність).

Наслідок із теореми Чебишова. Якщо всі члени послідовності незалежних однаково розподілених випадкових величин мають скінченні математичні сподівання і дисперсії , то для будь-якого

, (2')

тобто середнє арифметичне випадкових величин збігається за ймовірністю до математичного сподівання .