Запись алгоритма Евклида на языке с
/* Алгоритм Евклида */
#include <stdio.h>
#include <stdlib.h>
Int main() {
int m, n, r;
printf("Input m: "); scanf("%d", &m);
printf("Input n: "); scanf("%d", &n);
/* Е0. [Гарантировать, что m>n.] Если m<n, то m <-> n */
if (m<n) {r=m; m=n; n=r;}
while (1) {
/* E1. [Нахождение остатка.] Разделим m на n, и пусть остаток от деления будет равен r */
r=m%n;
/* Е2. [Сравнение с нулем.] Если r = 0, то завершить; n — НОД */
if (r==0) break;
/* ЕЗ. [Замещение.] Присвоить m <- n, n <- r и вернуться к E1 */
m=n; n=r;
}
printf("Greatest common divisor = %d \n", n);
exit(EXIT_SUCCESS);
}
Вопрос №3. Что такое «анализ алгоритмов»?
На практике нужны не просто алгоритмы, а хорошие алгоритмы в широком смысле этого слова. Одним из критериев качества алгоритма является время, необходимое для его выполнения; данную характеристику можно оценить по тому, сколько раз выполняется каждый шаг. Другими критериями являются адаптируемость алгоритма к различным компьютерам, его простота, изящество и т. д.
Часто решить одну и ту же проблему можно с помощью нескольких алгоритмов и нужно выбрать наилучший из них. Этими вопросами занимается важная область теоретического программирования - анализ алгоритмов. Предмет этой области состоит в том, чтобы для заданного алгоритма определить его рабочие характеристики.
Вопрос №4. Какие вопросы рассматривает теория алгоритмов?
Теория алгоритмов — это более широкая область, которая включает не только вопросы анализа алгоритмов, но и рассматривает формальные модели алгоритмов, вопросы существования или не существования эффективных алгоритмов решения определенных задач (алгоритмически неразрешимые проблемы), эквивалентность алгоритмов и др.
Вопрос №5. Сравнение эвристических и точных алгоритмов (на примере задачи коммивояжера).
Эвристический алгоритм «ближайшего соседа»
Начиная с произвольной точки p0, идем к ближайшей к ней точке (соседу) p1. От нее – к ее ближайшему еще не посещенному соседу (при этом точка p0 исключается из рассмотрения). Процесс повторяется до тех пор, пока не останется ни одной не посещенной точки, после чего мы возвращаемся в исходную точку p0, завершая маршрут.
Этот алгоритм прост в понимании, легко реализуется и достаточно эффективен, в общем, удовлетворяет всем свойствам алгоритма, но он совершенно неправилен! Т.е. получаемый с его помощью маршрут не обязательно будет самым коротким.
L=64
L=84
Эвристический алгоритм «ближайших пар»
Еще одна эвристика – соединять пары самых близких точек, если такое соединение не вызывает никаких проблем (досрочное завершение цикла или три пути из одной точки). Каждая вершина, еще не вошедшая в цепочку, рассматривается как самостоятельная «одновершинная» цепочка. Таким образом, на любом этапе выполнения этого алгоритма имеется множество отдельных вершин и множество не имеющих общих вершин цепочек, которые нужно соединить.
Общее количество искомых звеньев полного маршрута = n-1, поэтому алгоритм имеет вид цикла for i=1 to n-1 do, т.е. на каждом шаге отыскивается ровно одно звено, которое либо соединяет две отдельных вершины, либо «подключает» отдельную вершину к цепочке, либо соединяет две цепочки. За пределами цикла формируется последнее звено, соединяющее начало и конец единственной цепочки.
Этот алгоритм правильно работает на предыдущем примере:
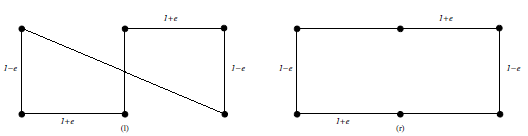
Однако на другом примере алгоритм ближайших пар работает неверно!
L=5-e+√(5+6e+5e2)
→ 7.24
L=6+2e
→ 6
