10. Классическое определение вероятности.

10. Операции над событиями

10. Теоремы сложения и умножения вероятности, совместные и несовместные события, зависимые и независимые события.

Теорема сложения вероятностей несовместных событий

Р(А+В) = Р(А)+Р(В)

Теорема сложения вероятностей совместных событий

Р(А+В) = Р(А)+Р(В) – Р(АВ)

Теорема умножения вероятностей независимых событий

Р(АВ)=Р(А) * Р(В)

Теорема умножения вероятностей зависимых событий

Р(АВ) = Р(А)*P(B|A) = P(B)*P(A|B)

Несовместные события А и В – если появление одного события исключает появление второго.

Совместные – если появление одного события не исключает появления второго.

События называются независимыми, если происхождение одного из них не зависит от того, произошло ли другое событие.

10. Формула полной вероятности, пример ее применения.

10. Формула Бернулли. Предельные теоремы Пуассона. Локальные и интегральные теоремы Муавра-Лапласса.

10. Определение случайной величины. Функция распределения случайной величины и её свойства.

10. Дискретные случайные величины и способы их задания. Ряд распределения.

10. Биномиальное и геометрическое распределения.

10. Распределение Пуассона

10. Непрерывные случайные величины способы их задания

10. Плотность распределения случайной величины и её свойства

10. Равномерное и показательное распределения

10. Нормальный закон распределения. Правило трёх сигм

31. Числовые характеристики случайных величин. Понятие о начальных и центральных моментах.

СВ помимо закона распределения могут также описываться числовыми характеристиками: МО, дисперсия, среднеквадратическое отклонение. Различают характеристики положения и характеристики рассеивания.

Мода дискретной СВ Х определяется как такое возможное значение Х_m, для которого

Мода дискретной СВ это наибольшее значение.

Модой непрерывной СВ Х называется действительное число d, определяемое как точка максимума плотности вероятности

Медианой непрерывной СВ Х называется действительное число h, удовлетворяющее условию

СВ Х называют центрированной если М(Х)=0.

СВ Х называется стандартизированной, если М(Х)=0, .

Начальным моментом k-го порядка распределения СВ Х называется действительное число , определяемое по формуле

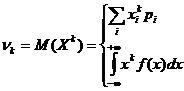
Центральным моментом k-го порядка распределения СВ Х называется число:

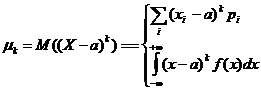, здесь а=М(Х).

32. Математическое ожидание случайной величины и его свойства.

33. Дисперсия СВ и её свойства и ср. квадратичная отклонение.

34. Понятие двумерной случайное величине. Функция распределения двумерной СВ и её свойства.

35. Распределение непрерывной случайной величины. Распределение компонент двумерной случайной величины.

36. Распределение непрерывной двумерной случайной величины. Совместная плотность распределения и распределение компонент в отдельности.

37. Условие независимости и коррелированности случайных величин. Связь между этими понятиями.

Случайные величины называются независимыми, если закон распределения одной из них не зависит от того какое значение принимает другая случайная величина. Понятие зависимости случайных величин является очень важным в теории вероятностей. Условные распределения независимых случайных величин равны их безусловным распределениям. Определим необходимые и достаточные условия независимости случайных величин.

Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих.

Две случайные величины X u Y называют коррелированными, если их корреляционный момент (или коэффициент корреляции) отличен от нуля; X u Y называют некоррелированными величинами, если их корреляционный момент равен нулю.

Две коррелированные величины также и зависимы. Обратное утверждение не всегда имеет место, т. е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, но может и равняться нулю.

Корреляционным моментом случайных величин и называют математическое ожидание произведения отклонений этих величин:

Для вычисления корреляционного момента дискретных величин используют формулу

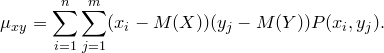
а для непрерывных величин

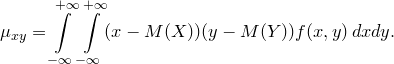
Корреляционный момент служит для характеристики связи между величинами и .

Теорема 5.3.

Корреляционный момент двух независимых случайных величин и равен нулю.

Из теоремы 5.3 следует, что если корреляционный момент двух случайных величин и не равен нулю, то и — зависимые случайные величины.

Коэффициентом корреляции случайных величин и называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

Очевидно, коэффициент корреляции двух независимых случайных величин равен нулю (так как ).