
- •Часть 1. Гидравлика
- •1. Свойства жидкостей.
- •1.1 Силы, действующие на жидкость. Давление в жидкости.
- •1.2. Основные свойства капельной жидкости.
- •1.2.1. Плотность и удельный вес.
- •1.2.2. Вязкость.
- •1.2.3. Сжимаемость.
- •1.2.4. Температурное расширение.
- •1.2.5. Испаряемость.
- •2. Гидростатика.
- •2 .1. Основной закон гидростатики.
- •2.2. Способы измерения давления.
- •2.3. Сила давления на плоскую горизонтальную и наклонную поверхности. Гидростатический парадокс.
- •3. Основные законы кинематики и динамики жидкости.
- •3.1. Понятия и определения.
- •3.2. Расход. Уравнение расхода.
- •3.3. Уравнение Бернулли для элементарной струйки идеальной жидкости.
- •3.4. Уравнение Бернулли для реальной (вязкой) жидкости.
- •4. Гидродинамическое подобие и режимы течения жидкости.
- •4.1. Основы гидродинамического подобия.
- •4.2. Режимы течения жидкости.
- •4.3. Кавитационное течение.
- •5. Гидравлические потери.
- •5.1. Потери на трение при ламинарном течении в трубах.
- •5.2. Потери на трение при турбулентном течении в трубах.
- •5.3. Потери в местных гидравлических сопротивлениях.
- •6. Истечение жидкости.
- •6.1. Истечение жидкости в атмосферу из малого отверстия в тонкой стенке при постоянном давлении. Коэффициенты сжатия , скорости , расхода .
- •6.2. Истечение жидкости через насадки.
- •7. Гидравлический расчет трубопроводов.
- •7.1. Гидравлический расчет просты трубопроводов.
- •7.2. Соединения простых трубопроводов. Сложный трубопровод.
- •7.2.1. Последовательное соединение простых трубопроводов.
- •7.2.2. Параллельное соединение простых трубопроводов.
- •7.2.3. Сложный трубопровод.
- •7.3. Трубопровод с насосной подачей.
- •8. Гидравлический удар.
- •Часть 2. Гидромашины и гидроприводы
- •9. Общие сведения o гидромашинах.
- •9.1. Основные понятия и общая классификация.
- •9.2. Основные параметры гидромашин.
- •10. Динамические гидромашины.
- •10.1. Классификация динамических насосов.
- •10.2. Характеристика и к.П.Д. Центробежного насоса.
- •10.3. Подобие лопастныx насосов и пересчет характеристик.
- •10.4. Кавитация и кавитационный расчет насосов.
- •10.5. Динамические гидродвигатели (гидротурбины).
- •11. Объёмные насосы.
- •11.1. Общие свойства и классификация объемных насосов.
- •11.2. Поршневые насосы.
- •11.3. Общие свойства и классификация роторных насосов.
- •11.4. Основные разновидности роторных насосов.
- •11.5. Основные параметры и характеристика роторного насоса
- •12. Объемные гидродвигатели.
- •12.1. Гидроцилиндры.
- •12.2. Гидромоторы.
- •13. Элементы объёмных гидроприводов.
- •13.1. Общие понятия и определения.
- •13.2. Гидропередачи.
- •13.3. Гидроаппараты.
- •13.3.1. Гидравлические дроссели.
- •13.3.2. Гидравлические клапаны.
- •13.3.3. Гидравлические распределители.
- •13.4. Вспомогательные гидравлические устройства.
- •14. Объёмные гидроприводы.
- •14.1. Гидропривод возвратно-поступательного движения
- •14.2. Гидропривод возвратно-поступательного движения
- •14.3. Гидропривод вращательного движения
- •14.4. Следящий гидропривод.
- •15. Гидродинамические передачи.
- •15.1. Гидромуфты.
- •15.1. Гидротрансформаторы.
3. Основные законы кинематики и динамики жидкости.
3.1. Понятия и определения.
Как было отмечено ранее, под термином "жидкость" будем понимать не только капельные жидкости, но и газы.
Установившееся течение - это течение, физические параметры которого (скорость, давление) неизменны по времени. Неустановившееся течение - это течение c переменными по времени физическими параметрами.
Линия тока - линия во всех точках которой вектор скорости направлен по касательной.

Элементарная струйка - часть потока жидкости бесконечно малых поперечных размеров.

Сечение (живое сечение) - поверхность нормальная к линиям тока.
Различают напорные и безнапорные течения жидкости. Напорными называют течения в закрытых руслах без свободной поверхности, а безнапорными - течения со свободной поверхностью. Примерами напорного течения могут служить течения в трубопроводах, гидромашинах или других гидроагрегатах. Безнапорными являются течения в реках, открыты каналах. В данном курсе рассматриваются напорные течения.
3.2. Расход. Уравнение расхода.
Расход - это количество жидкости, которое протекает через данное сечение в единицу времени. Количество жидкости можно измерять в единицах объема, массы или веса, в связи c чем различают объемный Q (м3/с), массовый Qm (кг/c) и весовой QG (Н/c) расходы. Между этими расходами существует такая же связь, как между объемом, массой и весом, т.е.
Qm = Q ∙ ρ ; QG = Q ∙ ρ ∙g ; QG = Qm ∙ g .
Расход связан со скоростью жидкости и площадью поперечного сечения S струйки или потока зависимостью
![]() (14)
(14)
Следует
отметить, что при течении реальной
(вязкой) жидкости, из-за трения между ее
слоями, скорости переменны по сечению
потока (рис.9). B этом 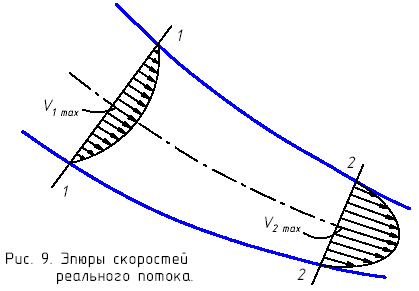 случае,
скорость, удовлетворяющую условию (14)
называют средней (
случае,
скорость, удовлетворяющую условию (14)
называют средней (![]() ).
Очевидно, что она лежит в пределах
от
=
0 до
=
).
Очевидно, что она лежит в пределах
от
=
0 до
=![]() .
.
Уравнение расходов представляет собой равенство расходов в двух сечениях потока (рис.9), т.е.
Q1 = Q2
или, с учетом (14),
![]() ,
(15)
,
(15)
где и S - средняя скорость и площадь соответствующего сечения.
Используя зависимость (15) можно найти среднюю скорость в любом сечении потока жидкости, если в каком-то сечении этого потока скорость уже известна и известны его геометрические размеры.
Уравнение расхода является законом сохранения массы для движущейся жидкости.
3.3. Уравнение Бернулли для элементарной струйки идеальной жидкости.
Рассмотрим установившееся течение идеальной жидкости, находящейся под действием лишь одной массовой силы - силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.
Возьмем одну из элементарных струек, составляющих поток, и выделим сечениями 1 и 2 участок этой струйки произвольной длины (рис. 10). Пусть площадь первого сечения равна dS1, скорость в нем 1, давление p1, а высота расположения центра тяжести сечения, отсчитанная от произвольной горизонтальной плоскости сравнения, z1. Во втором сечении соответственно dS2, 2, р2 и z2.
За бесконечно малый отрезок времени dt выделенный участок струйки переместится в положение 1' - 2'.
Применим к массе жидкости в объеме участка струйки теорему механики о том, что работа сил, приложенных к телу, равна приращению кинетической энергии этого тела. Такими силами в данном случае являются силы давления, действующие нормально к поверхности рассматриваемого участка струйки, и сила тяжести. Подсчитаем работу сил давления, силы тяжести и изменение кинетической энергии участка струйки за время dt.
чении положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы p1dS на путь 1dt:
p1dS1 1dt .
Рис.
10. Схема для вывода уравнения Бернулли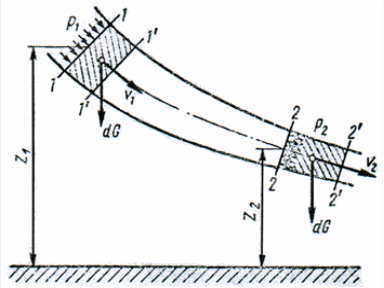
Работа силы давления во втором сечении имеет знак минус, так как направление силы прямо противоположно направлению перемещения, и определяется выражением
- p2dS2 2dt .
Силы давления, действующие по боковой поверхности отрезка струйки, работы не производят, так как они нормальны к этой поверхности а следовательно, нормальны и к перемещениям.
Итак, работа сил давления будет равна
p1 1dS1dt - p2 2dS2dt .
Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, поэтому надо из энергии положения жидкости в объеме 1 - 2 вычесть энергию положения жидкости в объеме 1' - 2'. При этом энергия положения промежуточного объема 1' - 2 сократится, и останется лишь разность энергий элементов 1 - 1', 2 - 2'. Если учесть уравнение расхода (15), то нетрудно заметить, что объемы, а следовательно, и силы тяжести заштрихованных элементов 1 - 1' и 2 - 2' равны между собой:
![]() .
.
Тогда
работа силы тяжести выразится как
произведение разности высот на силу
тяжести
![]() :
:
![]() .
.
Чтобы подсчитать приращение кинетической энергии рассматриваемого участка струйки за время dt, необходимо из кинетической энергии объема 1' - 2' вычесть кинетическую энергию объема 1 - 2. При вычитании кинетическая энергия промежуточного объема 1' - 2 сократится, и останется лишь разность кинетических энергий элементов 2 - 2' и 1 - 1', сила тяжести каждого из которого равна dG.
Таким образом, приращение кинетической энергии равно
![]() .
.
Сложив работу сил давления с работой силы тяжести и приравняв эту сумму приращению кинетической энергии получим
![]() .
.
Разделим это уравнение на dG, и произведя сокращения, получим
![]() .
.
Сгруппируем члены, относящиеся к первому сечению, в левой части уравнения, а члены, относящиеся ко второму сечению, в правой:
![]() ,
(16)
,
(16)
где
z
-
геометрическая
высота, или геометрический напop; p/(ρg)
- пьезометрическая высота,
или пьезометрический
напор;
![]() - скоростная
высота,
или
скоростной напор.
- скоростная
высота,
или
скоростной напор.
Полученное уравнение называется уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости. Оно было выведено Даниилом Бернулли в 1738 г.
Трехчлен вида
![]()
называется полным напором.
Уравнение Бернулли (16) записано для двух произвольно взятых сечений струйки и выражает равенство полных напоров H в этих сечениях. Так как сечения взяты произвольно, следовательно, и для любого другого сечения этой же струйки полный напор будет иметь то же значение:
![]() (вдоль
струйки)
(вдоль
струйки)
Итак, для идеальной движущейся жидкости сумма трех напоров (высот): геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.
