71. Определенный интеграл от непрерывной функции с переменным верхним пределом. Теорема о непрерывности. Доказательство.

Пусть функция f(x) интегрируема на [a,b]. Тогда, ∀x∈[a,b] каково бы ни было число x из [a,b], функция f(x) интегрируема и на сегменте [a,x]. Поэтому на интервале (a,b) определена функция F(x)=∫xaf(t)dt, которую называют интегралом с переменным верхним пределом.

Если функция f(x) интегрируема на интервале (a,b) ( => интегрируема на любом сегменте, содержащихся в интервале (a,b)), то интеграл с переменным верхним пределом представляет собой непрерывную на (a,b) функцию от верхнего предела. Чтобы убедиться в этом, докажем, что приращение ΔF(x)=F(x+Δx)−F(x)  функции F(x)=∫xcf(t)dt стремится к нулю при Δx→0 . В силу формулы среднего значения имеем ΔF(x)=F(x+Δx)−F(x)=∫x+Δxxf(t)dt=μ·∣ ∣ ∣ ∣  ∫X+ΔXXdt∣ ∣ ∣ ∣  =μ·Δx, где μ заключено между точной верхней и нижней гранями функции f(x) на сегменте [x,x+Δx]. Из последней формулы и вытекает, что ΔF→0  при Δx→0 . => непрерывна в каждой точке интервала(a,b).

72. Определенный интеграл от непрерывной функции с переменным верхним пределом. Производная. Доказательство. Вывод формулы Ньютона-Ле йбница.

Пусть функция f(x) интегрируема на [a,b]. Тогда, ∀x∈[a,b] каково бы ни было число x из [a,b], функция f(x) интегрируема и на сегменте [a,x]. Поэтому на интервале (a,b) определена функция F(x)=∫xaf(t)dt, которую называют интегралом с переменным верхним пределом.

Если f интегрируема на [a,b] и непрерывна в x0∈[a,b] , то F(x)=(∫xaf(t)dt)  дифференцируема вx0 и F′(x0)=f(x0) Было установлено существование производной от интеграла с переменным верхним пределом и доказано, что эта производная равна значению подынтегральной функции в точке, равной верхнему пределу, то есть

F′(x)=ddx∫xaf(t)dt=f(x).

Доказательство.

Докажем что limΔx→0ΔxF(x0+Δx)−F(x0)=f(x0). Для этого оценим ΔxΔF(x0)−f(x0). Заметим, что 1Δx∫xo+Δxxodt=1 и =>f(x0)=1Δx∫xo+Δxxof(x0)dt, ∣ ∣  ΔxΔF(x0)−f(x0)∣ ∣  =∣Δx∫x0+Δxx0f(t)dt−f(x0)∣ ∣  =∣ ∣ ∣ ∣  1Δx∫xo+Δxxo(f(t)−f(x0))dt∣ ∣ ∣ ∣  ≤ 1Δx∣ ∣ ∣ ∣  ∫x0+Δxx0∣ ∣  f(t)−f(x0)∣ ∣  dt∣ ∣ ∣ ∣   (1) Пусть задано ε>0. В силу непрерывности f в точке х0 ∃δ(ε)>0 , что если ∣ ∣  x−x0∣ ∣  <δ , и x∈[a,b]⇒∣ ∣  f(x)−f(x0)∣ ∣  <ε  (2) Выберем Δx так что ∣Δx∣<δ , тогда для значений t на отрезке по которому ведется интегрирование, будем иметь ∣ ∣  t−x0∣ ∣  ≤∣Δx∣<δ⇒ из (1)и(2) получим ∣ ∣  ΔxΔF(x0)−f(x0)∣ ∣  ≤ 1∣ΔX∣·ε∣ ∣ ∣  ∫xoxodt∣ ∣ ∣  =ε. Последнее означает, что limΔx→0ΔxF(x0+Δx)−F(x0)=f(x0) Чтд

73. Замена переменной и интегрирование по частям в определенном интеграле. Вывод формул.

Замена переменной в определённом интеграле. Теорема. Пусть функция

1. определена, непрерывно дифференцируема и монотонна на отрезке

,

2. ,

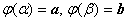3. функция

непрерывна на отрезке [a, b].

Тогда .

Док-во. Пусть F(x) - первообразная для функции f(x), т.е. , тогда - первообразная для функции . , что и требовалось доказать.

Формула интегрирования по частям для определённого интеграла. Если u(x), v(x) - непрерывно дифференцируемые функции, то . Док-во. Интегрируем равенство в пределах от a до b: . Функция в левом интеграле имеет первообразную uv, по формуле Ньютона-Лейбница , следовательно, , откуда и следует доказываемое равенство.