68. Интегральные суммы Дарбу. Теорема о существовании определенного интеграла. Доказательство для непрерывной подынтегральной функции.

Пусть функция f(x) определена на [a,b] и D={a=x0< x1<…< xn=b} разбиение отрезка [a,b]. Нижней суммой Дарбу называется сумма

s(f,D)= , mk = .

Верхней суммой Дарбу называется сумма

S(f,D)= , Mk = .

Если функция y = f(x) непрерывна на [a; b], то она интегрируема на этом отрезке.

69. Свойства определенного интеграла. Доказательство аддитивности определенного интеграла по промежутку интегрирования.

Свойства определенного интеграла.

[1]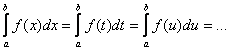

Предел в формуле (2) не зависит от обозначения переменной при вычислении интеграла.

[2]

[3]

[4]

[5] Свойство аддитивности

Теорема 1. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.

 В самом деле, будем при раздроблении промежутка [a, b] на части включать c в число точек деления. Если c = x_m, то

Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [a, b], [a, c] и [c, b]. Остается перейти к пределу при λ → 0.

  Доказанную теорему можно высказать в более общей форме. Для этого нам понадобится расширить смысл символа интеграла.

Если f(x) - любая функция, определенная в точке a, то по определению полагаем

     (1)

Таким образом, интеграл с совпадающими пределами равен нулю.

Пусть функция f(x) интегрируема на промежутке [a, b]. Тогда по определению полагаем

     (2)

Таким образом, при перестановке пределов интегрирования определенный интеграл меняет знак.

Теперь можем привести упомянутую более общую форму теоремы 1:

     Теорема 2.Пусть функция f(x) непрерывна в промежутке [A, B]. Если a, b, c суть точки этого промежутка, то

     (3)

     В самом деле, если из точек a, b и c две (а тем более три) совпадают, то равенство (3) очевидно. Пусть же все эти точки различны. Если a < c < b, то дело сводится к теореме 1. Прочие случаи взаимного расположения точек a, b, c тоже легко свести к той же теореме. Пусть, например, c < b < a. Тогда

откуда

и остается дважды применить формулу .

     Свойство интеграла, выражаемое теоремами 1 и 2, называется аддитивностью его, как функции промежутка интегрирования.

70. Теорема о среднем значении определенного интеграла от непрерывной функции. Доказательство.

Если f(x) - непрерывная функция, заданная на промежутке [a, b], то существует такая точка , что

     (1)

В самом деле, пусть M и m наибольшее и наименьшее значения f(x) на промежутке [a, b]. Составим для f(x) какую-нибудь интегральную сумму

Так как при всех k будет m ≤ f(ξ_k) ≤ M, а x_k+1 > x_k, то m(x_k+1 - x_k) ≤ M(x_k+1 - x_k). Складывая такие неравенства и замечая, что

получим:

m(b - a) ≤ σ ≤ M(b - a).

Переходя в этом неравенстве к пределу при λ → 0, приходим после деления на b - a к новому неравенству

     Таким образом, частное

есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции. Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [a, b] обязательно существует такая точка ξ, что h = f(ξ), а это равносильно равенству (1).

Заметим, что равенство (1) справедливо не только при a < b, но и при a = b (тогда обе части этого равенства нули), а также и при a > b (этот случай приводится к рассмотренному изменением знаков). В первом из этих случаев будет ξ = a, а во втором a ≥ ξ ≥ b.