56.Вероятно-статические основы формирования нормально распределенных случайных величин.

57.Центральная предельная Теорема Ляпунова и реализация ее требований при производстве геодезических измерений.

Теорема. Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

На практике для большинства случайных величин выполняются условия теоремы Ляпунова.

Центра́льные преде́льные теоре́мы (Ц.П.Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения.

Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины {Xi} имеют конечный третий момент. Тогда определена последовательность

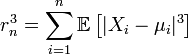Если предел

(условие Ляпунова),

58.Вероятнейшие поправки к результатам измерений. Понятие о принципе наименьших квадратов.

Вероятнейшей поправкой в случае равноточных измерений называется разность между Арифметической срединой являющейся вероятнейшим (наиболее надежным) значением, и отдельным результатом измерения, т.е. υ = L –ℓ . ( 3.31 ) Если арифметическая средина получена из n измерений, то можно написать n равенств вида (3.31). Сложив соответствующие части этих равенств, получим [υ] = nL – [ℓ ]. ( 3.32 ) Подставив вместо L его выражение L=[l]/n , найдем, что [υ] = 0. ( 3.33 ) Это Равенство выражает свойство вероятнейших поправок равноточных измерений

.Оно служит контролем правильности вычисления арифметической средины

- один из методов ошибок теории для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Н. к. м. применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений. Н. к. м. предложен К. Гауссом (С. Gauss, 1794-95) и А. Лежандром (A. Legendre, 1805-06). Строгое обоснование и установление границ содержательной применимости Н. к. м. даны А. А. Марковым и А. Н. Колмогоровым. В простейшем случае линейных связей (см. ниже) и наблюдений, не содержащих систематич. ошибок, а подверженных лишь случайным ошибкам, оценки неизвестных величин, полученные с помощью Н. к. м., являются линейными функциями от наблюденных значений. Эти оценки не имеют систематич. ошибок, т. е. являются несмещенными (см. Несмещенная оценка). Если случайные ошибки наблюдений независимы и подчиняются нормальному распределению, то Н. к. м. дает оценки неизвестных с наименьшей дисперсией, т. е. эти оценки являются эффективными (см. Статистическое оценивание). В этом смысле Н. к. м. является наилучшим среди всех остальных методов, позволяющих находить несмещенные оценки. Однако если распределение случайных ошибок существенно отличается от нормального, то Н. к. м. может и не быть наилучшим.

При обосновании Н. к. м. (по Гауссу) предполагается, что "убыток" от замены точного (неизвестного) значения нек-рой величины ее приближенным значением X, вычисленным по результатам наблюдений, пропорционален квадрату ошибки оптимальной оценкой считается такая лишенная систематич. ошибки величина X, для к-рой среднее значение "убытка" минимально. Именно это требование и составляет основу Н. к. м. В общем случае отыскание оптимальной в смысле Н. к. м. оценки X - задача весьма сложная, поэтому практически эту задачу сужают и в качестве Xвыбирают линейную функцию от результатов наблюдений, лишенную систематич. ошибки, и такую, для к-рой среднее значение убытка минимально в классе всех линейных функций. Если случайные ошибки наблюдений подчиняются нормальному распределению и оцениваемая величина mзависит от средних значений результатов наблюдений линейно (случай, весьма часто встречающийся в приложениях Н. к. м.), то решение этой задачи будет одновременно являться и решением общей задачи. При этом оптимальная оценка Xтакже подчиняется нормальному распределению со средним значением и, следовательно, плотность вероятности случайной величины X