9.Стандартная форма задачи линейного программирования

Задачами линейного программирования называются оптимизационные задачи, в которых ограничения, представленные в виде равенств или неравенств, и целевая функция линейна. Разработка модели ЛП включает следующие основные этапы: определение переменных задачи, представление её ограничений в виде линейных уравнений или неравенств, задание линейной целевой функции, подлежащей минимизации или максимизации.

Задача ЛП в стандартной форме с  m ограничениями и n  переменными имеет следующий вид:

максимизировать или минимизировать

при ограничениях:

.

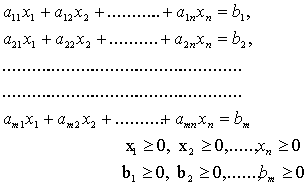Задачи ЛП в стандартной форме можно записать в компактных матричных обозначениях следующим образом:

максимизировать или минимизировать

при ограничениях

где A - матрица размерности mxn,  x - вектор-столбец  размерности nxl, b- вектор-столбец  размерности mxl, а c - вектор-строка размерности .1xn.

Обычно  A назначается матрицей коэффициентов,  x - вектором переменных,  b - вектором ресурсов, c - вектором оценок задачи ЛП.

При решении задачи ЛП симплекс-методом требуется, чтобы задача была представлена в стандартной форме. Однако не все практические задачи ее имеют, поэтому для удовлетворения требования алгоритма необходимо следующее.

• 1. При помощи введения дополнительных остаточных или избыточных переменных преобразовать неравенства в равенства.

• 2. Для получения неотрицательных переменных задачи неограниченные по знаку переменные заменить разностью двух неотрицательных.

При решении задач ЛП используются следующие основные понятия. Допустимым решением являются неотрицательные значения переменных, для которых выполняются ограничения, а допустимой областью - совокупность допустимых решений. Оптимальным решением называются такие допустимые значения переменных, при которых ЦФ экстремальна, т.е. имеет оптимальное значение. В ряде случаев, ЦФ имеет одно оптимальное значение при нескольких комбинаций значений переменных, следовательно, задача обладает неединственностью оптимума. Когда в задаче ЛП нет конечного оптимума, то в этом случае существует неограниченный оптимум.

10.Определение базисных решений стандартной задачи линейного программирования

Определение базисных решений стандартной задачи линейного программирования Рассмотрим задачу ЛП в канонической форме:

min cx                                (a)

Ax=b                                   (b)                                       

x≥0                                      .                                              (c)

Определение. Вектор x, удовлетворяющий системе линейных уравнений (b) , называется решением задачи ЛП.

Определение. Решение задачи ЛП, удовлетворяющее соотношению (c), называется допустимым решением задачи ЛП.

Определение. Допустимое решение задачи ЛП, доставляющее минимум целевой функции (a), называется оптимальным решением.

Определение. Решение задачи ЛП называется базисным, если векторы столбцы матрицы ограничений, соответствующие всем ненулевым координатам этого решения, образуют линейно независимую систему векторов.

Замечание. rkA=m  Определение. Допустимое базисное решение называется вырожденным, если число ненулевых координат в нем строго меньше, чем m=rk(A).

Определение. Задача ЛП называется вырожденной, если она имеет хотя бы одно вырожденное допустимое базисное решение.

Определение. m линейно независимых векторов столбцов матрицы ограничений A называются базисом, если они соответствуют всем ненулевым координатам некоторого допустимого базисного решения.

Пример.

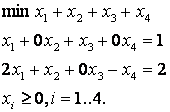
x1=(0,2,1,0) - базисное допустимое невырожденное решение,

x2=(0.5,1,0.5,0) - небазисное допустимое решение,

x3=(1,0,0,0)- базисное допустимое вырожденное решение,

x4=(0,1,1,-1) - небазисное недопустимое решение,

x5=(0,0,1,-2)- базисное недопустимое решение,

x6=(0,0,0,0)- не является решением данной задачи ЛП.

Теорема 1.  Множество всех допустимых решений задачи ЛП есть выпуклое замкнутое множество.

Теорема 2.  Если задача ЛП имеет допустимое решение, то она имеет и базисное допустимое решение.

Теорема 3. Пусть x=(x1,x2,…,xn) - допустимое решение задачи ЛП. x тогда и только тогда будет базисным допустимым решением задачи ЛП, когда точка x=(x1,x2,…,xn) является вершиной области допустимых решений этой задачи.

Теорема 4. Если задача ЛП имеет оптимальное решение, то она имеет и базисное оптимальное решение (без доказательства. Доказательство можно найти в [2]).

Фактически любое оптимальное решение может быть представлено в виде выпуклой линейной комбинации базисных оптимальных решений задачи ЛП.

В заключение данного параграфа рассмотрим следующую теорему:

Теорема 5. Пусть дана система m-мерных векторов  A1,A2,…,An ранга m (m<n) и A1,A2,…,Al,…,Am – ее базис. Заменим в этом базисе какой-нибудь из векторов, например, Al, на вектор Ak, k>m.Тогда полученная система векторов A1,A2,…,Ak,…,Am также является базисом этой системы тогда и только тогда, когда в разложении вводимого вектора Ak по базису A1,A2,…,Al,…,Am

коэффициент при заменяемом векторе Al отличен от нуля, то есть

xlk≠ 0.