8.Графический анализ чувствительности

Модель линейного программирования является как бы "моментальным снимком" реальной ситуации, когда параметры модели (коэффициенты целевой функции и неравенств ограничений) предполагаются неизменными. Естественным стремлением является изучить влияние изменения параметров модели на полученное оптимальное решение задачи ЛП. Такое исследование называется анализом чувствительности.

    Анализ моделей на чувствительность — это процесс, реализуемый после получения оптимального решения. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели.

    Например, в задаче об ассортименте продукции может представлять интерес вопрос о том, как повлияет на оптимальное решение увеличение и уменьшение спроса на продукцию или запасов исходного сырья. Возможно, также потребуется анализ влияния рыночных цен на оптимальное решение.

    При таком анализе всегда рассматривается комплекс линейных оптимизационных моделей. Это придает модели определенную динамичность, позволяющую исследователю проанализировать влияние возможных изменений исходных условий на полученное ранее оптимальное решение. Динамические характеристики моделей фактически отображают аналогичные характеристики, свойственные реальным процессам. Отсутствие методов, позволяющих выявлять влияние возможных изменений параметров модели на оптимальное решение, может привести к тому, что полученное (статическое) решение устареет еще до своей реализации.

    Анализ чувствительности может основываться на графическом решении задачи ЛП. Рассмотрим два случая:

• изменение коэффициентов целевой функции;

• изменение значений констант в правой части неравенств ограничений.

На этом шаге будем проводить анализ модели на чувствительность к изменению значений коэффициентов целевой функции.

    В общем виде целевую функцию задачи ЛП с двумя переменными можно записать следующим образом: z = с₁x₁ + с₂х₂

    Изменение значений коэффициентов c₁ и c₂ приводит к изменению угла наклона прямой z. Графический способ решения задачи ЛП показывает, что это может привести к изменению оптимального решения: оно будет достигаться в другой угловой точке пространства решений. Вместе с тем, очевидно, существуют интервалы изменения коэффициентов c₁ и c₂, когда текущее оптимальное решение сохраняется.

    Задача анализа чувствительности и состоит в получении такой информации. В частности, представляет интерес определение интервала оптимальности для отношения c₁/c₂ (или, что то же самое, для c₂/c₁); если значение отношения c₁/c₂ не выходит за пределы этого интервала, то оптимальное решение в данной модели сохраняется неизменным.

    Следующий пример показывает, как можно получить необходимый результат с помощью анализа графического представления модели ЛП.

    Пример 1. Применим процедуру анализа чувствительности к модели для компании "Русские краски". На рис. 1 видно, что функция z = 5х₁ + 4х₂ достигает максимального значения в угловой точке С.

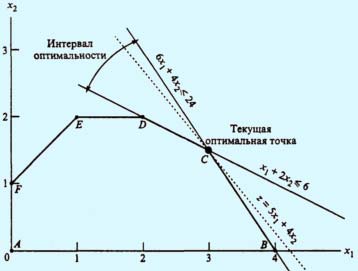Рис. 1. Анализ чувствительности

    При изменении коэффициентов целевой функции z = с₁x₁ + с₂х₂ точка С останется точкой оптимального решения до тех пор, пока угол наклона линии z будет лежать между углами наклона двух прямых, пересечением которых является точка С. Этими прямыми являются 6х₁ + 4х₂ = 24 (ограничение на сырье Ml) и х₁ + 2х₂ = 6 (ограничение на сырье М2).

    Алгебраически это можно записать следующим образом:

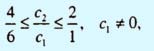или

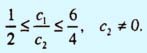
    В первой системе неравенств условие c₁ <> 0 означает, что прямая, соответствующая целевой функции, не может быть горизонтальной.

    Аналогичное условие в следующей системе неравенств означает, что эта же прямая не может быть вертикальной.

    Из рис. 1 видно, что интервал оптимальности данной задачи (он определяется двумя прямыми, пересекающимися в точке С) не разрешает целевой функции быть ни горизонтальной, ни вертикальной прямой. Таким образом, мы получили две системы неравенств, определяющих интервал оптимальности в нашем примере. (Когда c₁ и c₂ могут принимать нулевые значения, интервал оптимальности для отношения c₁/c₂ (или c₂/c₁ ) необходимо разбить на два множества, где знаменатели не обращались бы в нуль.

    Итак, если коэффициенты c₁ и c₂ удовлетворяют приведенным выше неравенствам, оптимальное решение будет достигаться в точке С.

    Отметим, если прямая z = с₁x₁ + с₂х₂ совпадет с прямой х₁ + 2х₂ = 6, то оптимальным решением будет любая точка отрезка CD.

    Аналогично, если прямая, соответствующая целевой функции, совпадет с прямой 6x₁ + 4х₂ = 24, тогда любая точка отрезка ВС будет оптимальным решением. Однако заметим, что в обоих случаях точка С остается точкой оптимального решения.

    Приведенные выше неравенства можно использовать при определении интервала оптимальности для какого-либо одного коэффициента целевой функции, если предположить, что другой коэффициент остается неизменным. Например, если в нашей модели зафиксировано значение коэффициента с₂ (пусть с₂ = 4), тогда интервал оптимальности для коэффициента с₁ получаем из неравенств 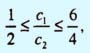путем подстановки туда значения с₂ = 4. После выполнения элементарных арифметических операций получаем неравенства для коэффициента с₁: 2 ≤ с₁ ≤ 6.

    Аналогично, если зафиксировать значение коэффициента с₁ (например, с₁ = 5), тогда из неравенств 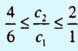получаем интервал оптимальности для коэффициента с₂: 10/3 ≤ с₂ ≤ 10.

    На следующем шаге рассмотрим расчет стоимости сырья - еще один способ анализа модели на чувствительность.

На этом шаге мы рассмотрим анализ модели на чувствительность и определим стоимость ресурсов задачи линейного программирования.

    Во многих моделях линейного программирования ограничения трактуются как условия ограниченности ресурсов. В таких ограничениях правая часть неравенств является верхней границей количества доступных ресурсов. Рассмотрим чувствительность оптимального решения к изменению ограничений, накладываемых на ресурсы.

    Такой анализ задачи ЛП предлагает простую меру чувствительности решения, называемую стоимостью единицы ресурса; при изменении количества доступных ресурсов (на единицу) значение целевой функции в оптимальном решении изменится на стоимость единицы ресурса.

    Проиллюстрируем этот вид анализа задачи ЛП на следующем примере.

    Пример 1. В модели для компании "Русские краски" первые два неравенства представляют собой ограничения на использование сырья M1 и М2 соответственно. Определим стоимость единиц этих ресурсов.

    Начнем с ограничения для сырья M1. Напомним, что в данной задаче оптимальное решение достигается в угловой точке С, являющейся точкой пересечения прямых, соответствующих ограничениям на сырье M1 и М2 (рис. 1).

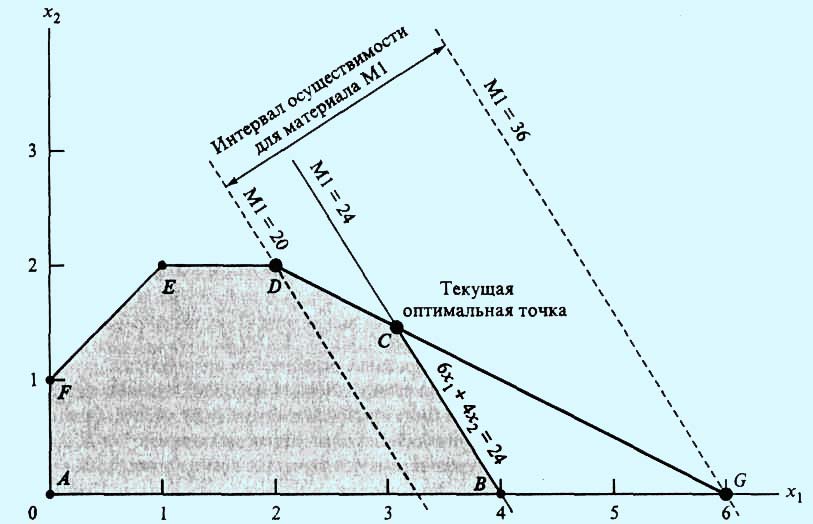Рис. 1. Стоимость ресурса М1

    При изменении уровня доступности материала M1 (увеличение или уменьшение текущего уровня, равного 24 т) точка С оптимального решения "плывет" вдоль отрезка DG. Любое изменение уровня доступности материала M1, приводящее к выходу точки пересечения С из этого отрезка, ведет к неосуществимости оптимального решения в точке С. Поэтому можно сказать, что концевые точки D = (2, 2) и G = (6, 0) отрезка DG определяют интервал осуществимости для ресурса M1. Количество сырья M1, соответствующего точке D = (2, 2), равно 6x₁ + 4x₂ = 6*2 + 4*2 = 20 т.

    Аналогично количество сырья, соответствующего точке G = (6, 0), равно 36 т.

    Таким образом, интервал осуществимости для ресурса M1 составляет 20 ≤ M1 ≤ 36 (здесь через M1 обозначено количество материала M1). Если мы определим М1 как M1 = 24 + D₁, где D₁ — отклонение количества материала М1 от текущего уровня в 24 т, тогда последние неравенства можно переписать как 20 ≤ 24 + D₁ ≤ 36 или -4 ≤ D₁ ≤ 12. Это означает, что текущий уровень ресурса M1 может быть уменьшен не более чем на 4 т и увеличен не более чем на 12 т. В этом случае гарантируется, что оптимальное решение будет достигаться в точке С — точке пересечения прямых, соответствующих ограничениям на ресурсы M1 и М2.

    Теперь вычислим стоимость единицы материала M1. При изменении количества сырья M1 от 20 до 36 тонн, значения целевой функции z будут соответствовать положению точки С на отрезке DG. Обозначив через y₁ стоимость единицы ресурса M1, получим следующую формулу:

    Если точка С совпадает с точкой D = (2, 2), то z = 5*2 + 4*2 = 18 (тысяч д.e.), если же точка С совпадает с точкой G = (6, 0), тогда z = 5*6 + 4*0= 30 (тысяч д.e.). Отсюда следует, что

(тысяч д.е. на тонну материала M1).

   Этот результат показывает, что изменение количества ресурса M1 на одну тонну (если общее количество этого ресурса не меньше 20 и не больше 36 тонн) приводит к изменению в оптимальном решении значения целевой функции на 750 д.е.

   Теперь рассмотрим ресурс М2.

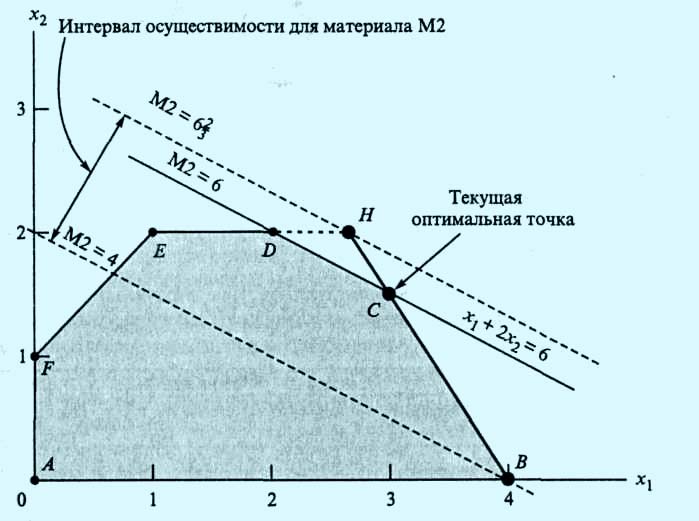Рис. 2. Стоимость ресурса М2

    На рис. 2 видно, что интервал осуществимости для ресурса М2 определяется концевыми точками В и H отрезка ВН, где В = (4, 0) и Н= (8/3, 2). Точка Н находится на пересечении прямых ED и ВС. Находим, что количество сырья М2, соответствующего точке В, равно x₁ + 2х₂ = 4 + 2*0 = 4 т, а точке Н — 8/3+2*2= 20/3 т. Значение целевой функции в точке В равно 5x₁ + 4х₂ = 5*4 + 4*0 = 20 (тысяч д.e.), а в точке Н — 5*8/3 + 4*2 = 64/3 (тысяч д.e.). Отсюда следует, что количество сырья М2 может изменяться от 4 до 20/3 тонн, а стоимость единицы ресурса М2, обозначенная как у₂, равна

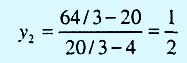(тысяч д.е. на тонну материла M2).