Некоторые практически важные законы распределения.

Закон равномерной плотности

Равномерная плотность распределения определяется выражением:

f(x)

f(x)={0, если х<α: 1/β- α

f (x)={1/β- α, если α<x< β

f (x)={0, если x> β

0 α β х

F(x)=∫(от -∞ до +∞) f(t)dt={0, x< α; ∫(от x до α)dt/ β- α=1/ β- α*t|=x- α/ β- α, если α<x< β; 1, если x< β

F(x)1

0 α β x

MedX= β- α/2; ModX=не сущ

mx=M[x]= ∫(от -∞ до +∞) xf(x)dx=∫(от α до β)x/β- αdx=(β- α)( β+ α)/2

Дисперсия Dx=ὴ2=M[(x-mx)^2f(x)dx=1/β- α∫(от α до β)(x- β+ α/2)dx=…=(β- α)^2/12

Dx=(β- α)^2/12; f(x)

Ϛ x=√Dx=(β- α)/2√3

0 α a b β

P(a<x<b)=b-a/ (β- α)

Закон редких явлений. Распределение Пуассона.

Согласно теореме о повторении опытов (теорема Бернулли)

Лекция 11 от 23.11.11

Нормальный закон распределения. Закон Гаусса

Главная особенность этого закона в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Рассмотрим непрерывную случайную величину Х. Нормальный закон распределения случайной величины Х характеризуется плотностью вероятности вида:

F(x)=(1/E*(2pi)^-2)e, где m и δ-параметры.

Г рафик функции f(x)

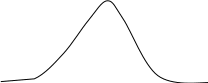
m x

Вычислим мат. Ожидание:

mx=M[X]=(1/E*(2pi)^-2) m=mx

Вычислим дисперсию

Dx=D[X]= (1/E*(2pi)^-2)∫(от -∞ до +∞)(х-mx)dx

Вероятность попадания нормально распр. Случ. Величины. На заданный участок. Функция Лапласса

Функция распределения для закона Гаусса имеет вид:

F[x]=P[X<x]

Принято обозначать нормальный закон распределения случайной величины Х через характеристики mδ²

X~N(m,δ^2)

Рассмотрим неопределенный интеграл

I=∫e^{-(x-m)^2/ mδ^2}dx и сделаем подстановку.

x-m/r=t

dx=δdt

Этот неопределенный интеграл не выражается через элементарные функции, поэтому функция распределения f(x) может быть записана следующим образом:

F(x)=1/δ(2pi)^-2)*∫e^{-t^2/2}dt (1)

Необходимо вычислить табличным образом функцию вида (1), рассматривая при этом функцию

Ф(Z)=1/(2pi)^-2)*∫(от -∞ до Z) e^t²/2dt (2)

Функция Ф(Z) – функция Лапласа или интеграл вероятностей

Ф(Z)=1/(2pi)^-2)*∫(от ∞ до Z) e^t²/2dt

То Ф(Z) есть функция распределения нормально распределенной случайной величины < c нулевым М.О. m=0 и единичной дисперсией δ²=1

P[Z<z]=Ф[Z]

Нормальное распределение с параметрами m=0 и δ²=1 называют стандартным нормальным распределением и обозначают

N(0,1)

Оно описывается функцией распределения, представляющую собой функцию Лапласа

Рассмотрим случайную величину.

Z=(X-m)/δ, где Х~N(m,δ^2)

Очевидно, что Z нормально распределен.

Легко показать, что она имеет нулевое М.О. и единичную дисперсию

Следовательно, она описывается функцией распределения вида 2-функций Лапласа.

Найдем связь между функциями распределения случайной величины X и Z. Из формулы (1) и (2) следует, что функция нормальной случайной величины Х может быть выражена через функцию Лапласа.

F(x)=Ф(Z)|_z=x-m/δ=Ф(x-m/δ), где m=M[X], δ²=D[X] (3)

Из (3) следует, что вероятность попадания нормального распределения случайной величины в интервале [α;β] может быть выражен через функцию Лапласа:

p(α<x<β)=F(β)-F(α)=Ф(β-m/δ)-Ф(α-m/δ)