9 Вопрос

Однородные системы линейных уравнений. Условие существования нетривиальных решений. Фундаментальная система решений однородной системы.

Система линейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свободные члены(В) равны 0.

Система линейных однородных уравнений всегда совместна, т.к. она всегда имеет, по крайней мере, нулевое (тривиальное) решение(0,0,0…0).

Система линейных однородных уравнений имеет НЕТРИВИАЛЬНЫЕ решения тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при r(A)<n.

Свойства решений:

1. Если строка e₁=(k_1…k_n) -решение системы, то и строка αe₁=( αk_1… αk_n)-также решение этой системы

2. Если строки e₁=(k_1…k_n) и e₂=(l_1…l_n)-решения системы, то при любых с₁, с_2­ их линейная комбинация с₁*e₁+с₂*e₂-также решения этой системы.

Всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы.

Система линейно независимых решений e₁..e_n называется фундаментальной, если каждое решение системы является линейной комбинацией решений e₁..e_n.

Если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений меньше числа переменных n, то всякая фундаментальная система решений системы состоит из n-r решений.

Общее решение системы линейных однородных уравнений имеет вид:

с₁*e₁+с₂*e₂+…+c_k*e_k, где e₁,e_k-любая фундаментальная система решений, а c₁, c_k-любые произвольные числа, k=n-r/

Т.Е. общее решение системы m линейных уравнений с n переменными равно сумме общего решения соответствующей ей системы однородных линейных уравнений и произвольного частного решения этой системы.

10 Вопрос

Собственные векторы и собственные числа квадратной матрицы. Свойства собственных векторов. Понятие присоединенного вектора

Определение 9.3. Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: Ах = λх, то есть результатом применения к х линейного преобразования, задаваемого матрицей А, является умножение этого вектора на число λ. Само число λ называется собственным числом матрицы А.

Подставив в формулы (9.3) x`j = λxj, получим систему уравнений для определения координат собственного вектора:

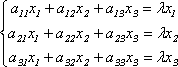Отсюда

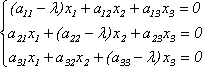
Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде: 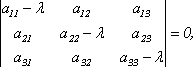получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить так:

| A - λE | = 0 поскольку в его левой части стоит определитель матрицы А-λЕ. Многочлен относительно λ | A - λE| называется характеристическим многочленом матрицы А.

Свойства характеристического многочлена:

1) Характеристический многочлен линейного преобразования не зависит от выбора базиса. 2) Если матрица А линейного преобразования является симметрической (т.е. аij=aji), то все корни характеристического уравнения– действительные числа.

Свойства собственных чисел и собственных векторов:

1) Если выбрать базис из собственных векторов х1, х2, х3, соответствующих собственным значениям λ1, λ2, λ3 матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:

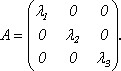
2) Если собственные значения преобразования А различны, то соответствующие им собственные векторы линейно независимы.

3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.