
- •1.Перечислите и поясните основные этапы полного построения алгоритмов.
- •6. Программная реализация алгоритма.
- •4.Сформулируйте основные определения абстрактного алфавита (алфавит, слово алфавита, расширение алфавита, алфавитный оператор).
- •7.Дайте определение алгоритма, его особенности.
- •13.Свойства и виды алгоритмов и соотношение между ними.
- •14.Интерпретации и модели.
- •15.Семантическая и формальная непротиворечивость.
- •1) «Условие – действие», т.Е. Если построенные объекты удовлетворяют некоторым условиям, то для построений нового объекта нужно выполнить такое-то действие;
- •Первая теорема о неполноте
- •22. Интуитивное понятие алгоритма. Требования к алгоритмам.
- •23. Формализация понятия алгоритма и универсальные алгоритмические модели.
- •24.Машина Тьюринга - основные определения. Понятие вычислимости на машине Тьюринга.
- •25.Операции над машинами Тьюринга. Универсальная машина Тьюринга.
- •26.Понятие алгоритмической неразрешимости. Теорема Райса.
- •27.Проблема остановки - формулировка теоремы и ее доказательство.
- •28.Понятие рекурсии. Примитивно-рекурсивные функции. Примеры.
- •29.Неограниченный оператор минимизации. Примеры. Определение частично-рекурсивной функции.
- •30.Разрешимые и перечислимые множества и предикаты.
- •31.Конечные автоматы. Основные определения. Способы задания автоматов.
- •32.Алгоритмические возможности: что могут и что не могут вычислять автоматы. Примеры.
- •33.Эквивалентность автоматов. Алгоритм минимизации автоматов.
- •34.Автоматы и логические схемы. Программная реализация автоматов.
- •35.Интуитивное определение понятия «алгоритм». Свойства алгоритма.
- •37. Приметивно рекурсивные функции
- •Глава 4. Алгоритмы
- •40 Частично рекурсивные функции
- •41 Рекурсивные функции
- •Проблемы, касающиеся абстрактных машин
- •Другие проблемы
- •Проблемы, алгоритмическая неразрешимость которых не доказана
- •42 Формулировка и доказательство критерия Поста
- •Описание
- •Примеры Пример 1
- •Пример 2
- •Ветвление (условный оператор)
- •Повторение (цикл)
- •Устройство машины Тьюринга
- •Проблемы, касающиеся абстрактных машин
- •Другие проблемы
- •Проблемы, алгоритмическая неразрешимость которых не доказана
- •48) Машина Поста
- •Принцип работы
- •Устройство машины Тьюринга
- •Описание машины Тьюринга
- •Полнота по Тьюрингу
- •Варианты машины Тьюринга
- •Машина Тьюринга, работающая на полубесконечной ленте
Варианты машины Тьюринга
Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.
Машина Тьюринга, работающая на полубесконечной ленте
В качестве примера такого сведения рассмотрим следующую теорему: Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте.
Рассмотрим доказательство, приведённое Ю. Г. Карповым в книге «Теория автоматов». Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте:
![]()
Затем перенумеруем ячейки, причём будем считать, что символ «*» не содержится в словаре МТ:
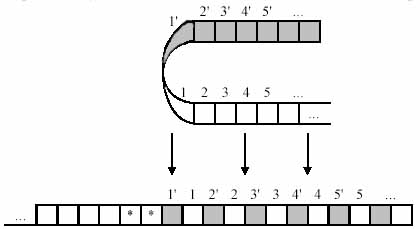
Наконец, изменим машину Тьюринга, удвоив число её состояний, и изменим сдвиг головки считывания-записи так, чтобы в одной группе состояний работа машины была бы эквивалентна её работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе МТ встретится символ ‘*’, значит головка считывания-записи достигла границы зоны:
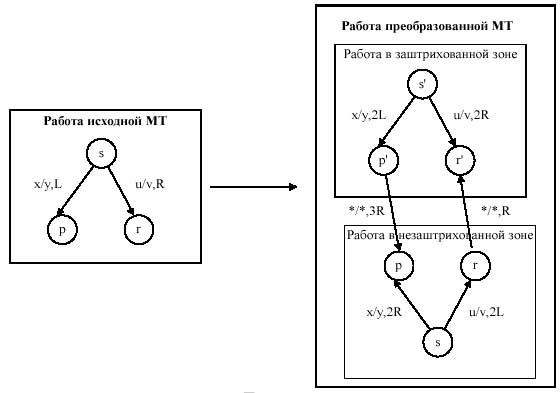
Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации. Очевидно, что слева от ограничивающих маркеров «*» лента в эквивалентной машине Тьюринга не используется.
49) Машины с неограниченными регистрами (МНР)
Выбранный нами гипотетический компьютер называется машиной с неограниченными регистрами (МНР) [Катленд,1983,16-29]; он является легким видоизменением машин, впервые рассмотренных Дж.Шепердсоном и Х.Стерджисом (1963) и получивших название РАМ (равнодоступная адресная машина) и РАСП (равнодоступная адресная машина с хранимой программой). Эти модели в большей степени, чем машина Тьюринга отражают структуру современных вычислительных устройств.
МНР содержит бесконечное число регистров, обозначаемых через R1,R2,R3,..., каждый из которых в любой момент времени содержит некоторое натуральное число, причём число, содержащееся в Rn, будем обозначать через rn. Это можно изобразить следующим образом:
МНР может изменять содержимое регистров с помощью некоторой команды. Каждая команда может быть одного из следующих четырех видов: команда обнуления, команда прибавления единицы, команда переадресации и команда условного перехода (см.таблицу 1).
Таблица 1. Команды МНР и их операционная семантика
Арифметическими командами назовём команды обнуления, прибавления единицы и переадресации, причём команды Z(n) и S(n) соответствуют простейшим операциям над натуральными числами в формальной арифметике.
Программа МНР - это конечная последовательность команд. Начальной конфигурацией называется последовательность a1,a2,...
натуральных чисел, содержащихся в регистрах R1,R2,....
Чтобы МНР приступила к вычислениям (работе), она должна быть снабжена программой P и начальной конфигурацией.
Пусть P«(I1,I2,...Is), где I1,I2,...Is - последовательность команд. Вначале МНР выполняет команду I1.
Определим индуктивно понятие "следующая команда в вычислении".
Определение.
(1) I1 - следующая команда в вычислении.
(2) Если Ik (k=1,2,...,s-1) не является командой условного
перехода, то команда Ik+1 является следующей командой в вычислении.
(3) Если Ik (k=1,2,...,s-1) является командой J(m,n,q), а rm и rn - текущее содержимое регистров Rm и Rn соответственно, то следующей командой в вычислении является команда Iq, q=1,2,...,s, если rm=rn, и команда Ik+1 - в противном случае.
(4) Если Is является командой J(m,n,q), а rm и rn - текущее содержимое регистров Rm и Rn соответственно, то следующей командой в вычислении является команда Iq, если rm=rn и q£s.
(5) Никаких других следующих команд в вычислении нет.
Определение.
Будем говорить, что следующая команда отсутствует, если:
(1) Is является арифметической командой;
(2) Is является командой J(m,n,q), причём rm=rn и q>s;
(3) Is является командой J(m,n,q), причём rm¹rn. В этом случае говорят, что вычисление остановилось после выполнения команды Is, а заключительной конфигурацией будем называть последовательность r1,r2,r3,... содержимых регистров на этом шаге.
Определение.
Будем говорить, что вычисление останавливается, если следующая команда отсутствует.
МНР работает, пока вычисление не остановится.
Предложение.
Для каждой команды переадресации T(m,n) существует программа, не содержащая команд переадресации, которая на всякой конфигурации МНР дает тот же результат, что и T(m,n).
Доказательство. Упражняйтесь!
Таким образом, команда переадресации в определении МНР является избыточной; тем не менее, представляется естественным и удобным иметь такие команды, т.к. они облегчают построение программ.
Замечание.
Сравните МНР с машиной с регистрами общего назначения (см.[Уокерли,1984,с.184-192]
Маши́на Тью́ринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен
