37. Приметивно рекурсивные функции

Примитивно рекурсивные функции Введем следующие функции

оп(хи...,хп) = 0,1т(Х1, ..., Хп) = Хт A < ТО < П\\ П= 1, 2, ...),называемые далее простейшими.

Пусть даны частичные функции д : Nn —? N и h : Nn+2 —? N.

Частичная функция / : Nn+l —? N получена из функций д, h примитивной рекурсией, если f(xu...,xn,0) = д(хи...,хп),f(xi,..., хп,у + 1) = h(xi,..., хп,у, f(xi,..., хп,у)).

Для п = 0 уравнения D.1) принимают вид (д = const = a)

/@) = а, f(x + l)=h(x,f(x)).

Как видно из этих уравнений, задав исходные данные

(«1, ...,х„, 0), можно шаг за шагом найти значения функции для (x-L,...,xn,\\),(xi_,...,xn,2),...,(x-L,...,xn,m),...

Символически задание / через примитивную рекурсию можно

записать как Частичная функция / : Nn+l —? N называется примитивно рекурсивной относительно множества частичных функций ?], если /получается из функций множества ?] и простейших функций конечным числом операций подстановки (суперпозиции) и примитивной рекурсии.

Если ?] = 0, то примитивно рекурсивная относительно

множества частичных функций 5^ функция получается только из простейших функций и поэтому ее называют просто примитивно рекурсивной.

Нетрудно понять, что примитивно рекурсивные функции

являются всюду определенными функциями.

Пример 4.1. Функция f(x,y) = х + у примитивно рекурсивна.

В самом деле,

f(x, у + 1) = х + (у + 1) = (х + у) + 1 = sl(x + у) = sl(f(x, у)).

Это означает, то функция х + у строится из примитивно рекурсивных функций l\\,h{x, y,z) = z + 1 = sl(z) с помощью примитивной рекурсии.

Поэтому х + у примитивно рекурсивная функция.

Пример 4.2. Функция f(x,y) = xy примитивно рекурсивна.

Действительно,

f(x,0)=x-0 = o1(x),

f(x, у + 1) = х(у + 1) = ху + х = f(x, у) + х.

D.3)

Если взять

g(x) = ol(x), h(x,y,z)=z + x

и вспомнить, что h — это примитивно рекурсивная функция (пример 4.1),то убеждаемся в примитивной рекурсивности функции ху.

Частично рекурсивные функции

Пусть дана частичная функция / : Nn —± N. Зафиксируем данные(xi,...,xn). Введем функцию

М/(ж1,...,ж„) =min{f(x1,...,xn-1,y) = хп}.

yEN

По существу, М - это операция на множестве частичных функций.Результатом является новая частичная функция с тем же числом аргументов. Назовем эту операцию минимизацией.

Пример 4.3. Функция

,х)= f я-1, х>0,

v \\ не определено, X = 0

— частично рекурсивна.

Действительно,

д(х) = Ms1(x) = min{s1(y) = у + 1 = х}.

Следовательно, д получена из простейшей функции s1 с помощью операции минимизации.

Глава 4. Алгоритмы

Частичная функция / : Nn+1 -? N называется частично

рекурсивной относительно множества частичных функций ?], если получается из функций множества ?] и простейших функцийконечным числом операций подстановки (суперпозиции),примитивной рекурсии и минимизации.

Если ?] = 0, то частично рекурсивная относительно множества частичных функций 5^ функция получается только из простейших функций, и поэтому ее называют просто частично рекурсивной.

Каждая примитивно рекурсивная функция является частично

рекурсивной. Обратное неверно, поскольку в класс частично рекурсивных функция в соответствии с определением попадают частичная функция Ms1 и, например, нигде не определенная функция

/(ж) = тт{ж + 1 + у = 0}.

J/6JV

Обратим внимание на то, что минимизация может быть

организована как последовательный (алгоритмический) процесс.

Действительно, последовательно находим

/(Ж1, ..., Ж„-1, 0),/(Ж1, ..., Ж„-1, 1), ...,/(Ж1, ..., Ж„-1, у), ...

Наименьшее о, для которого

- это значение для M/(a;i,..., ж^).1

38) По­ми­мо двух осно­вных опе­ра­ций (под­ста­но­вки и при­ми­тив­ной ре­кур­сии), ис­по­ль­зу­ют­ся и дру­гие опе­ра­ции, со­хра­ня­ющие при­ми­тив­ную ре­кур­сив­ность фун­кций. Эти опе­ра­ции яв­ля­ют­ся про­из­во­дны­ми от осно­вных, т.е. мо­гут быть по­лу­че­ны из них и эле­мен­тар­ных фун­кций.

Пусть име­ют­ся фун­кции y₁,y₂,...,y_k, и в ре­зу­ль­та­те не­ко­то­рой опе­ра­ции Á над эти­ми фун­кци­ями по­лу­че­на фун­кция j, т.е. j=Á(y₁,...,y_k).

Опре­де­ле­ние [Мат­ро­сов,1989,с.23].

Опе­ра­ция Á на­зы­ва­ет­ся при­ми­тив­но-ре­кур­сив­ной опе­ра­ци­ей, ес­ли из ра­вен­ст­ва j=Á(y₁,y₂,...,y_k) сле­ду­ет, что j яв­ля­ет­ся при­ми­тив­но-ре­кур­сив­ной фун­кци­ей от­но­си­те­ль­но со­во­куп­но­сти {y₁,y₂,...,y_k}.

Рас­смо­трим при­ме­ры час­то при­ме­ня­емых при­ми­тив­но-ре­кур­сив­ных опе­ра­ций, сле­дуя В.Л.Матросову [1989,с.23-24].

1. Опе­ра­ция вве­де­ния фик­тив­ных пе­ре­мен­ных Пусть за­да­на фун­кция g(x,y) и пусть j(x,y,z)=g(x,y). В этом слу­чае го­во­рят, что фун­кция j по­лу­че­на из фун­кции g опе­ра­ци­ей вве­де­ния фик­тив­ной пе­ре­мен­ной z.

Предложение.

Фун­кция j яв­ля­ет­ся при­ми­тив­но-ре­кур­сив­ной фун­кци­ей от­но­си­те­ль­но со­во­куп­но­сти {g}.

Доказательство.

j(x,y,z)=g(I₁³(x,y,z),I₂³(x,y,z))=Sub₂³(g;I₁³,I₂³).

Предложение доказано.

2. Опе­ра­ция под­ста­но­вки кон­стант Пусть за­да­на фун­кция g(x,y,z) и пусть j(x,y)=g(x,y,a). В этом

слу­чае го­во­рят, что фун­кция j по­лу­ча­ет­ся из фун­кции g опе­ра­ци­ей под­ста­но­вки кон­стант.

 

Предложение.

Фун­кция j(x,y) яв­ля­ет­ся при­ми­тив­но-ре­кур­сив­ной фун­кци­ей от­но­си­те­ль­но со­во­куп­но­сти {g}.

Доказательство.

j(x,y)=g(I₁²(x,y),I₂²(x,y),C_a²(x,y))=Sub₃²(g;I₁²,I₂²,C_a²).

Предложение доказано.

3. Опе­ра­ция про­из­во­ль­ной под­ста­но­вки Пусть фун­кции h₁,h₂ и h₃ яв­ля­ют­ся фун­кци­ями, за­ви­ся­щи­ми лишь от не­ко­то­рых пе­ре­мен­ных x,y,z. Го­во­рят, что фун­кция j(x,y,z) по­лу­че­на из фун­кций g,h₁,h₂,h₃ опе­ра­ци­ей про­из­во­ль­ной под­ста­но­вки (су­пер­по­зи­ции), ес­ли j=g(h₁,h₂,h₃).

Пример.

Пусть да­ны фун­кции, опре­де­лён­ные тер­ма­ми g(x₁,x₂,x₃), h₁(x), h₂(x,y), h₃(x,y,z), а j(x,y,z)=g(h₁(x),h₂(x,y),h₃(x,y,z)).

По­ка­жем, что j(x,y,z) - при­ми­тив­но-ре­кур­сив­ная фун­кция от­но­си­те­ль­но со­во­куп­но­сти {g,h₁,h₂,h₃}. Фун­кцию j мож­но пред­ста­вить так:

j(x,y,z)=g(h₁(I₁³(x,y,z)),h₂(I₁³(x,y,z),I₂³(x,y,z)), h₃(I₁³(x,y,z),I₂³(x,y,z),I₃³(x,y,z))).

Обоз­на­чим:

h₁^*(x,y,z)«h₁(I₁³(x,y,z)), h₂^*(x,y,z)«h₂(I₁³(x,y,z),I₂³(x,y,z)), h₃^*(x,y,z)«h₃(I₁³(x,y,z),I₂³(x,y,z),I₃³(x,y,z)).

Фун­кции h₁^* и h₂^* по­лу­че­ны из фун­кций h₁ и h₂ со­от­ве­т­ст­вен­но опе­ра­ци­ей вве­де­ния фик­тив­ных пе­ре­мен­ных, по­это­му h₁^* - при­ми­тив­но-ре­кур­сив­ная фун­кция от­но­си­те­ль­но {h₁}, h₂^* - при­ми­тив­но-ре­кур­сив­ная фун­кция от­но­си­те­ль­но {h₂}. Оче­вид­но, h₃^* - при­ми­тив­но-ре­кур­сив­ная фун­кция от­но­си­те­ль­но со­во­куп­но­сти {h₃}. А т.к. вы­пол­ня­ет­ся ра­вен­ст­во j=Sub₃³(g;h₁^*,h₂^*,h₃^*), то j яв­ля­ет­ся при­ми­тив­но-ре­кур­сив­ной фун­кци­ей от­но­си­те­ль­но со­во­куп­но­сти {g,h₁^*,h₂^*,h₃^*}. При­ме­няя пер­вое свой­ст­во от­но­си­те­ль­ной при­ми­тив­ной ре­кур­сив­но­сти, по­лу­ча­ем, что j яв­ля­ет­ся при­ми­тив­но-ре­кур­сив­ной фун­кци­ей от­но­си­те­ль­но со­во­куп­но­сти фун­кций {g,h₁,h₂,h₃}.

4. Опе­ра­ции ко­неч­но­го сум­ми­ро­ва­ния и ко­неч­но­го про­из­ве­де­ния

 

Опре­де­ле­ние [Мат­ро­сов,1989,с.25].

(1) Го­во­рят, что фун­кция f(x₁,...,x_n,y) по­лу­че­на из фун­кции g(x₁,...,x_n,z) в ре­зу­ль­та­те опе­ра­ции ко­неч­но­го сум­ми­ро­ва­ния, ес­ли для лю­бо­го на­бо­ра зна­че­ний пе­ре­мен­ных (x₁,...,x_n,y)

f(x₁,...,x_n,y)=g(x₁,...,x_n,0)+g(x₁,...,x_n,1)+...+g(x₁,...,x_n,y).

В да­ль­ней­шем бу­дем при­ме­нять сле­ду­ющее обоз­на­че­ние:

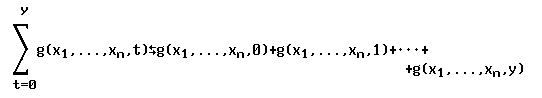
(2) Го­во­рят, что фун­кция f(x₁,...,x_n,y) по­лу­че­на из фун­кции g(x₁,...,x_n,z) в ре­зу­ль­та­те опе­ра­ции ко­неч­но­го про­из­ве­де­ния, ес­ли для лю­бо­го на­бо­ра пе­ре­мен­ных (x₁,...,x_n,y)

f(x₁,...,x_n,y)=g(x₁,...,x_n,0)×g(x₁,...,x_n,1)×...×g(x₁,...,x_n,y).

В да­ль­ней­шем бу­дем ис­по­ль­зо­вать сле­ду­ющее обоз­на­че­ние:

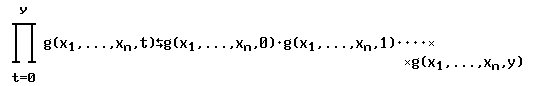
Пред­ло­же­ние [Мат­ро­сов,1989,с.25-26].

Опе­ра­ции ко­неч­но­го сум­ми­ро­ва­ния и ко­неч­но­го про­из­ве­де­ния при­ми­тив­но-ре­кур­сив­ны от­но­си­те­ль­но со­во­куп­но­сти {g}

Доказательство.

Рас­смо­трим опе­ра­цию ко­неч­но­го сум­ми­ро­ва­ния. Пусть

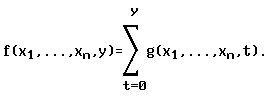
Тог­да име­ет мес­то сле­ду­ющая сис­те­ма ра­венств:

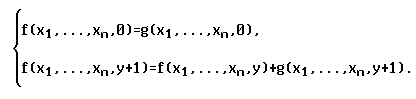
Тог­да фун­кцию f мож­но пред­ста­вить как ре­зу­ль­тат при­ми­тив­ной ре­кур­сии, т.е. f=Rec(g₁,h), где:

g₁«g(I₁ⁿ(x₁,...,x_n),...,I_nⁿ(x₁,...,x_n),0), h(x₁,...,x_n,y,z)«gïI₁ ⁿ⁺² (x₁,...,x_n,y,z),...,I_n^{n+2 (x}₁,...,x_n,y,z),

I_n+1 ^{n+2 (x}₁,...,x_n,y,z)+1ï+I_n+2 ^{n+2 (x}₁,...,x_n,y,z).

Дей­ст­ви­те­ль­но, лег­ко про­ве­рить, что име­ют мес­то ра­вен­ст­ва:

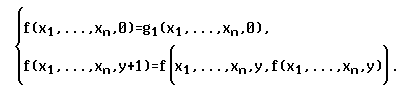
Из спо­со­ба за­да­ния фун­кций g₁ и h сле­ду­ет, что g₁ и h яв­ля­ют­ся при­ми­тив­но-ре­кур­сив­ны­ми фун­кци­ями от­но­си­те­ль­но со­во­куп­но­сти {g}. Оче­вид­но фун­кция f, пред­став­ля­ющая ре­зу­ль­тат при­ми­тив­ной ре­кур­сии над фун­кци­ями g₁ и h, так­же при­ми­тив­но-ре­кур­сив­на от­но­си­те­ль­но со­во­куп­но­сти, со­сто­ящей из од­ной фун­кции g.

Ана­ло­гич­но мож­но про­вес­ти до­ка­за­те­ль­ст­во и для опе­ра­ции ко­неч­но­го про­из­ве­де­ния.

Предложение доказано (для операции конечного суммирования).

След­ст­вие [Мат­ро­сов,1989,с.26].

Опе­ра­ции ко­неч­но­го сум­ми­ро­ва­ния и ко­неч­но­го про­из­ве­де­ния со­хра­ня­ют при­ми­тив­ную ре­кур­сив­ность фун­кций.

39) Рекурсивный предикат – предикат P типа

для которого вычислима по Тьюрингу соответствующая характеристическая функция



Рекурсивными множествами являются многие обычные множества натуральных чисел: множество четных чисел, множество простых чисел и т.д.

Множество называется рекурсивно перечислимым, если оно является множеством значений некоторой вычислимой функции.

Рекурсивно перечислимый предикат – предикат P рекурсивно перечислим, если существует процедура, позволяющая устанавливать истинность P(x1,…xk); если же P(x1,…xk) ложно, то эта процедура иногда будет это устанавливать, а иногда будет продолжаться неограниченно долго.

Теорема.2. Применение логических связок , , ¬ к рекурсив-

ным предикатам дает рекурсивные же предикаты.

Теорема.2. Применение квантора к рекурсивному предикату приводит к рекурсивному же предикату.

Интуитивно предикат Р рекурсивен, если существует алгоритм, позволяющий выяснить для каждого набора {x1,…xk} слов истинно P(x1,…xk) или нет.

Обычно арифметические предикаты x  y, x + y = z, “x – простое число”, “х делит у” являются рекурсивными.

Здесь и далее под вычислимыми функциями будут подразумеваться одноместные вычислимые функции.

Рассмотрим свойства рекурсивных и перечислимых множеств.

Теорема.3. Объединение и пересечение рекурсивных множеств рекурсивны; дополнение к рекурсивному множеству рекурсивно.

Ввиду известного соответствия между теоретикомножественными операциями и пропозициональными связками эта теорема немедленно вытекает из следующей теоремы.

Теорема.3. Дизъюнкция и конъюнкция вычислимых предикатов вычислимы; отрицание вычислимого предиката вычислимо.

Теорема 3. справедлива для предикатов любой вместимости; мы, однако, докажем ее только для одноместных предикатов – этого достаточно, чтобы получить теорему 3. Для общего случая теорема

доказывается аналогично.

Теорема 4. Объединение и перечисление перечислимых множеств перечислимы.

Теорема 5. Множество тогда и только тогда перечислимо, когда оно является областью определения некоторой вычислимой функции.

Теорема.6. Множество A является рекурсивно перечислимым тогда и только тогда, когда существует разрешимый предикат R x y ( , )

такой, что x A  тогда и только тогда, когда

yR x y ( , ).

Теорема.7. Всякое разрешимое множество рекурсивно перечислимо.

Теорема8 (теорема Поста). Множество тогда и только тогда разрешимо, когда оно само и его дополнение рекурсивно перечислимы.

Теорема 9. Множество номеров самоприменимых машин Тьюринга рекурсивно перечислимо, но не азрешимо. Поскольку мы обычно отождествляем слово с его номером, вместо множества номеров мы можем говорить здесь о множестве кодов.

Теорема 10. Существуют непересекающиеся рекурсивно перечислимые множества E1 и E2 такие, что никакое разрешимое множество не может содержать E1, не имея при этом общих точек с E2. (Как иногда говорят, E1 и E2 не отделимы разрешимыми множествами.)