
- •Элементы линейной алгебры
- •1)Матрицы и операции над ними
- •Основные действия над матрицами
- •Транспонирование матриц
- •Обратная матрица
- •Вычислительная сложность
- •Свойства обратной матрицы
- •Способы нахождения обратной матрицы
- •Точные (прямые) методы Метод Гаусса—Жордана
- •С помощью матрицы алгебраических дополнений
- •Использование lu/lup-разложения
- •Примеры Матрица 2х2
- •8) Ранг матрицы
- •9) Теорема Кронекера-Капелли.
- •10) Метод Гаусса.
- •2. Векторная алгебра и аналитическая геометрия в пространстве
- •1) Линейные операции над векторами
- •2) Проекция вектора на ось, свойства проекции
- •4) Деление отрезка в данном отношении
- •11) Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.
- •12) Параметрические уравнения прямой
- •13) Угол между прямыми
- •14) Угол между прямой и плоскостью
- •1)Комплексные числа. Модуль и аргумент.
- •Комплексные равенства (Сформулируйте смысл комплексного равенства)
- •Геометрическое изображение комплексных чисел (в чём состоит геометрическое изображение комплексных чисел?)
- •Модуль и аргумент комплексного числа (Что такое модуль и аргумент комплексного числа?)
- •2)Алгебраическая и тригонометрическая формы комплексного числа (Что такое алгебраическая и тригонометрическая формы комплексного числа?)
- •Основные свойства умножения
- •Деление комплексных чисел
- •Возведение комплексного числа в натуральную степень
- •Извлечение корня натуральной степени из комплексного числа
- •4)Формулы Эйлера. Формула Муавра
- •Рациональные функции
- •1.Рациональные дроби. Теорема Безу
- •2.Простейшие дроби
- •3. Разложение правильной рациональной дроби на простейшие
- •4. Метод неопределенных коэффициентов
Транспонирование матриц
Определение. Матрицу АТ называют транспонированной матрицей А, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы АТ.(т.е. строки матрицы А заменены на столбцы и наоборот)
А
=
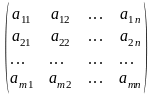 ; АТ=
; АТ=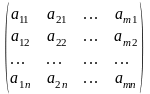 ;
;
Пример: Даны матрицы
А =
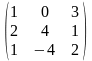 ,
В =
,
В =
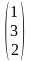 ,
С =
,
С =
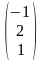 и число
= 2. Найти АТВ+С.
и число
= 2. Найти АТВ+С.
AT
=
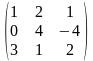 ; ATB
=
=
; ATB
=
=
 =
=
 ;
;
C
=
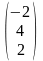 ;
АТВ+С
=
+
=
;
АТВ+С
=
+
=
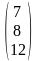 .
.
Пример: Даны матрицы
А =
 и В =
и В =
 .
Найти произведение матриц АВ и ВА.
.
Найти произведение матриц АВ и ВА.
АВ
=
=
 .
.
ВА = = (21 + 44 + 13) = (2 + 16 + 3) = (21).
Пример: Найти
произведение матриц А=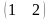 ,
В =
,
В =
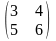
АВ
=
=
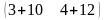 =
=
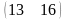 .
.
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к элементам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
5) транспонирование
Обратная матрица
Определение:
Матрица
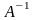 называется обратной по отношению к
квадратной матрице
называется обратной по отношению к
квадратной матрице
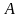 ,
если
,
если
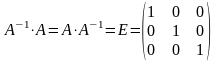 .
.
Обратная матрица существует только для квадратной матрицы, определитель которой не равен нулю. Такая матрица называется невырожденной.
Рассмотрим общий подход к нахождению обратной матрицы.
Рассмотрим на примере, как найти обратную матрицу .
Пусть
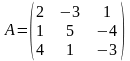
1)Найти определитель матрицы
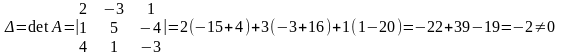 .
.
Так как
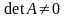 ,
то обратная матрица
существует.
,
то обратная матрица
существует.
2) Сформировать матрицу из алгебраических дополнений каждого элемента матрицы.
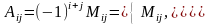
если
 - четное число,
- четное число,
если - нечетное число.

3) Транспонируем матрицу из алгебраических дополнений.
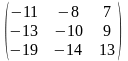 .
.
4) Обратная матрица определяется формулой
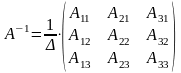 ,
,
 .
.
2)Умножение матриц
Умножить матрицу А на матрицу В можно только в том случае, когда количество столбцов матрицы А равно числу строк матрицы В. Поэтому, для ввода размерности матриц необходимо указать только число строк и столбцов матрицы А и число столбцов матрицы В, а количество строк программа подставит автоматически. Произведением будет матрица С, элементы которой равны сij=∑aik·bki, где aik,bki- элементы матриц А и В соответственно.
Что бы более наглядно увидеть, как производит вычисления наша программа, приведем пример:
|
· |
|
= |
|
Запишем, как нашли каждый элемент новой матрицы
C11=a11·b11+a12·b21=-5·2.5+8·13=92 C12=a11·b12+a12·b22=-5·6+8·12=66 C13=a11·b13+a12·b23=-5·11+8·(-10)=-135 C14=a11·b14+a12·b24=-5·12+8·1=-52 C21=a21·b11+a22·b21=9·2.5+10·13=153 C22=a21·b12+a22·b22=9·6+10·12=174 C23=a21·b13+a22·b23=9·11+10·(-10)=-1 C24=a21·b14+a22·b24=9·12+10·1=118 C31=a31·b11+a32·b21=-14·2.5+5·13=30 C32=a31·b12+a32·b22=-14·6+5·12=-24 C33=a31·b13+a32·b23=-14·11+5·(-10)=-204 C34=a31·b14+a32·b24=-14·12+5·1=-163
3) Определители второго порядка и их свойства
Определитель транспонированной матрицы равен определителю исходной матрицы.
Если в определителе какие-либо две строки (столбца) равны между собой, то такой определитель равен 0.
Общий множитель всех элементов какой-либо строки (или столбца) можно выносить за знак определителя.
Если поменять в определителе местами какие-либо две строки (столбца), то определитель меняет знак.
Если все элементы какой-либо строки (столбца) определителя равны 0, то такой определитель равен 0.
Если к элементам какой-либо строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца) этого же определителя, умноженные на одно и то же число, то определитель не изменяется.
4)Миноры
Миноры матрицы
Пусть дана квадратная матрица А, n - ого порядка. Минором некоторого элемента аij ,определителя матрицы n - ого порядка называется определитель (n - 1) - ого порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент аij. Обозначается Мij.
Рассмотрим на примере определителя матрицы 3 - его порядка:
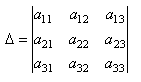
, тогда согласно определению минора, минором М12, соответствующим элементу а12, будетопределитель:
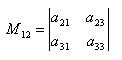
При этом, с помощью миноров можно облегчать задачу вычисления определителя матрицы. Надо разложить определитель матрицы по некоторой строке и тогда определитель будет равен сумме всех элементов этой строки на их миноры. Разложение определителя матрицы 3 - его порядка будет выглядеть так:
|
|
, знак перед произведением равен (-1)n, где n = i + j.
Алгебраические дополнения:
Алгебраическим дополнением элемента аij называется его минор, взятый со знаком "+", если сумма (i + j) четное число, и со знаком "-", если эта сумма нечетное число. Обозначается Аij. Аij = (-1)i+j × Мij.
Тогда можно переформулировать изложенное выше свойство. Определитель матрицы равен сумме произведение элементов некторого ряда (строки или столбца) матрицы на соответствующие им алгебраические дополнения.
5.Определители 3 порядка методы вычисления
Определение через разложение по первой строке
Метод треугольников
6) Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.
Описание метода
Для системы n линейных уравнений с n неизвестными (над произвольным полем)
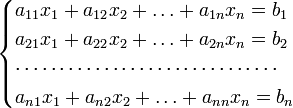
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде
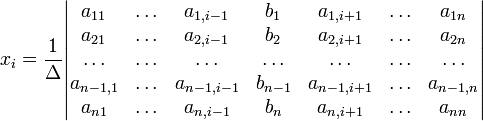
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
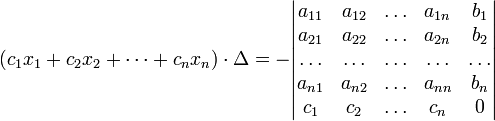
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,...,bn и x1,x2,...,xn, либо набор c1,c2,...,cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде
формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Пример
Система линейных уравнений:
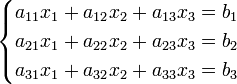
Определители:
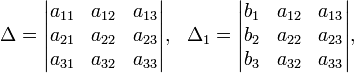
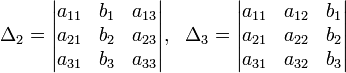
Решение:
![]()
Пример:
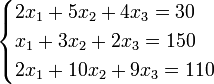
Определители:
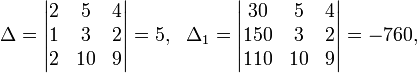
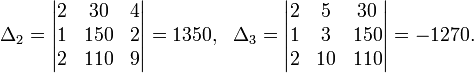
![]()
