Гармоническая линеаризация при симметричных колебаниях

Рассмотрим структурную схему системы (рис. и), приведенную к простейшему виду. Схема состоит из линейной части (ЛЧ) практически любого порядка и нелинейного элемента (НЭ).

Допустим, что в этой замкнутой системе при x₃(t)=0 установился режим автоколебаний с частотой ₀. Тогда все координаты системы x(t), (t), z(t) представляют собой периодические функции времени с периодом Т=2/₀. Колебания всех

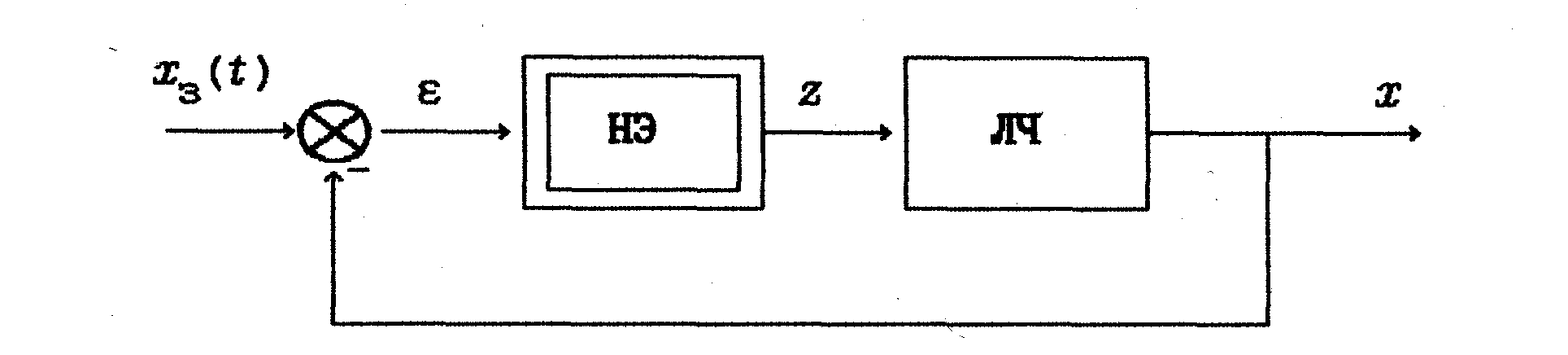
Рис.2. Структурная схема CAP с нелинейным элементом

переменных нелинейны и всегда могут быть представлены в вида бесконечного ряда гармоник с частотами колебаний пЫд (n=1,2,. . . 00, ₀-основная частота).

Если нелинейный элемент значительно отличается от линейной зависимости, то высшие гармоники имеют относительно большую величину и ими, строго говоря, нельзя пренебречь. Однако линейная часть, как правило, является фильтром низких частот и плохо пропускает высшие гармоники. Это позволяет сделать допущение, что сигнал x(t) синусоидальный:

.

При нулевом задающем воздействии x(t)=-(t), поэтому на входе нелинейного элемента также будет действовать синусоидальный сигнал с частотой ₀ и амплитудой .

Реакции двух из типовых нелинейных элементов на синусоидальный сигнал приведены на рис.3.

Колебании на выхода этих нелинейных элементов имеют несинусоидальный характер и могут быть представлены в вида гармонического колебания основной частоты ₀ и бесконечного ряда высших гармоник. Но поскольку на выхода линейной части высшие гармоники выражены весьма слабо, то и при определении сигнала на выхода нелинейного элемента можно принимать во внимание только первую гармонику.

Предположение о гармоническом характере автоколебаний позволяет по аналогии с линейными системами ввести понятие о передаточной функции (комплексном коэффициенте передачи) нелинейного элемента как отношения первой гармоники выходного сигнала нелинейного элемента к входному синусоидальному сигналу (рис.4).

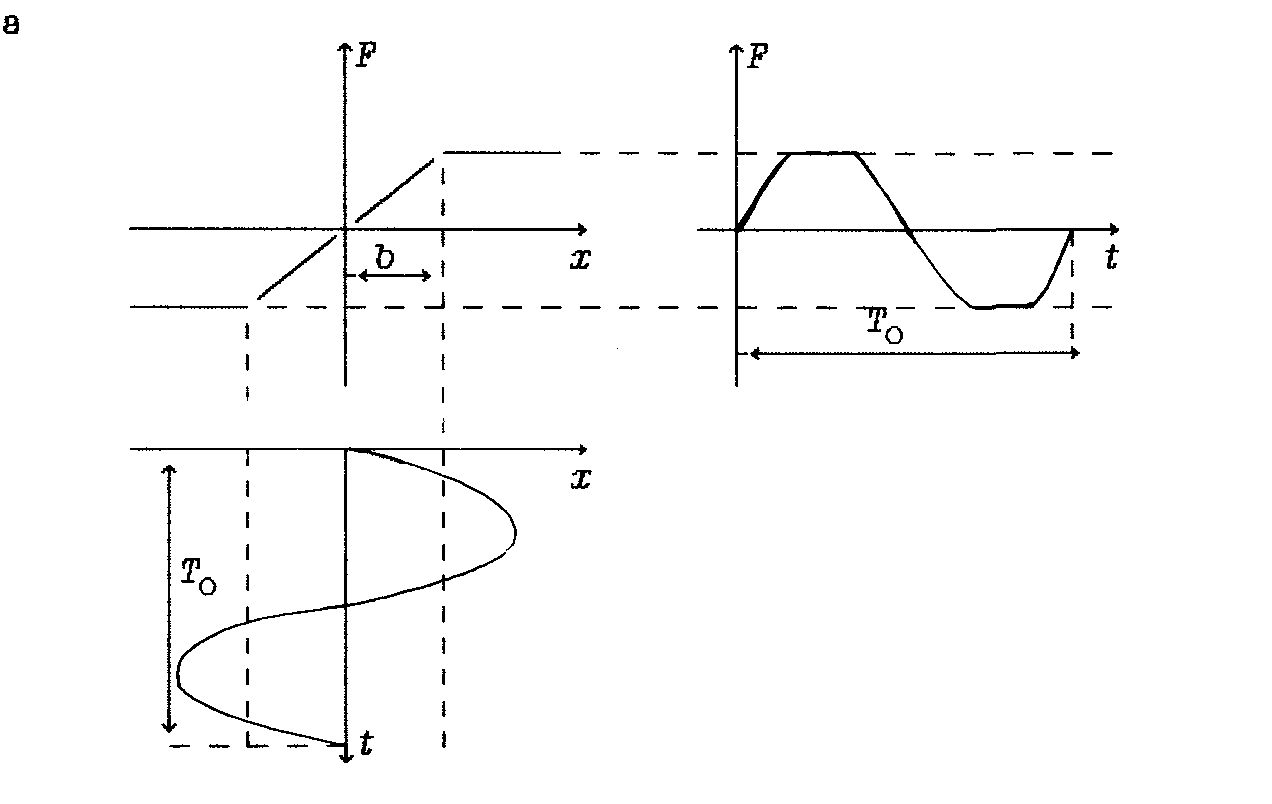
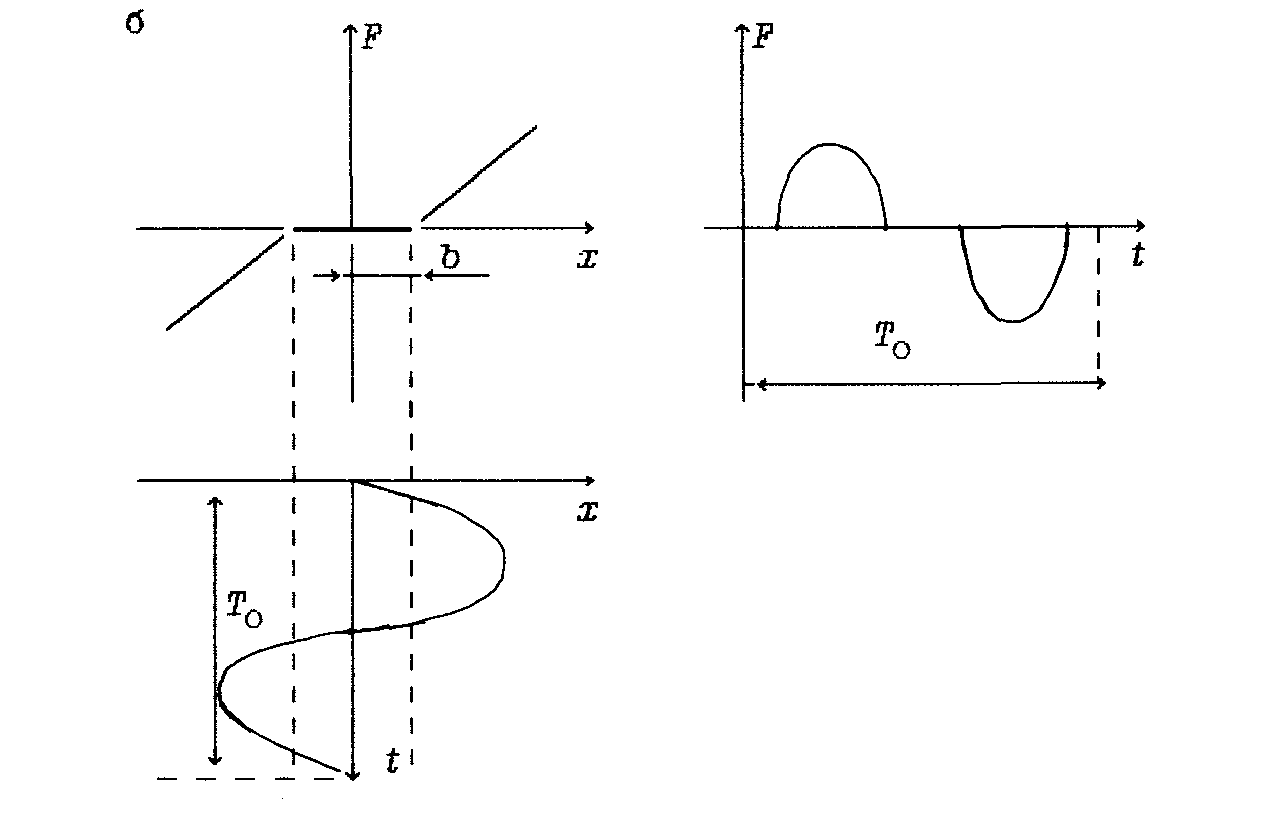
Рис 3. Реакции нелинейных элементов типа "ограничение" (а) и "зона нечувствительности" (б) на синусоидальный сигнал

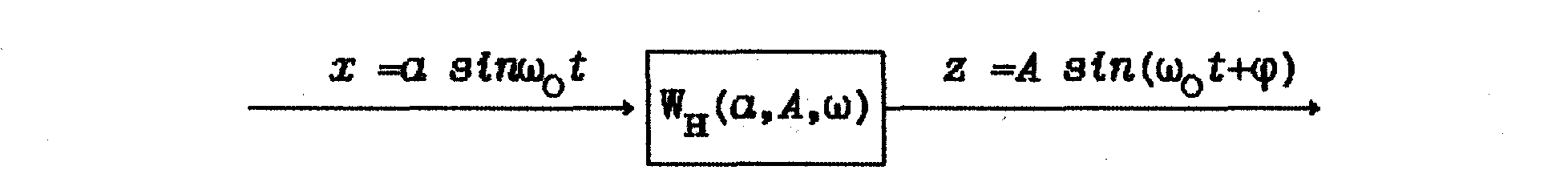
Рис. 4. Структурная схема гармонически линеаризованного нелинейного элемента

В комплексной форме записи получим

В самом общем случае W_н является функцией частоты, входной и выходной амплитуд.

Ограничимся рассмотрением случая, когда нелинейность статическая. Тогда

т.е. передаточная функция нелинейного элемента зависит от амплитуда входного сигнала  и не зависит от его частоты ₀. Следует также заметить, что если передаточная функция линейной системы W_Л(j) исчерпывающе описывает ее свойства, то W_н() служит лишь для приближенного исследования и не может описать всех свойств нелинейного элемента (в частности, не позволяет представить состава высших гармоник на его выхода).

Замену фактически нелинейной связи между входом и выходом нелинейного элемента линейной называют гармонической линеаризацией. Гармоническая линеаризация нелинейностей позволяет выявить автоколебательные режимы, оценить их устойчивость, исследовать качество процесса регулирования.

Рассмотрим методику определения передаточных функций нелинейных элементов для случая симметричных колебаний на выхода звена. Для статической однозначной нелинейности W_н() можно представить в вида

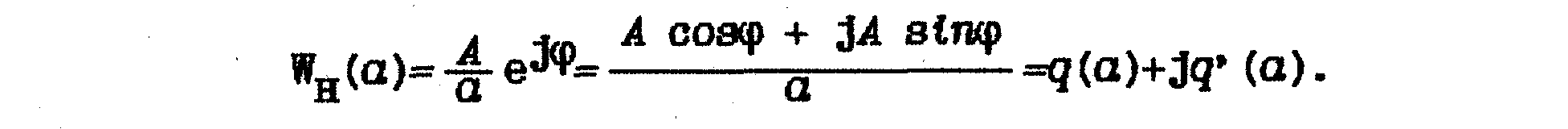
Коэффициенты гармонической линеаризации q и g^, первой гармоники выходной переменной z определяются из следующих выражений:

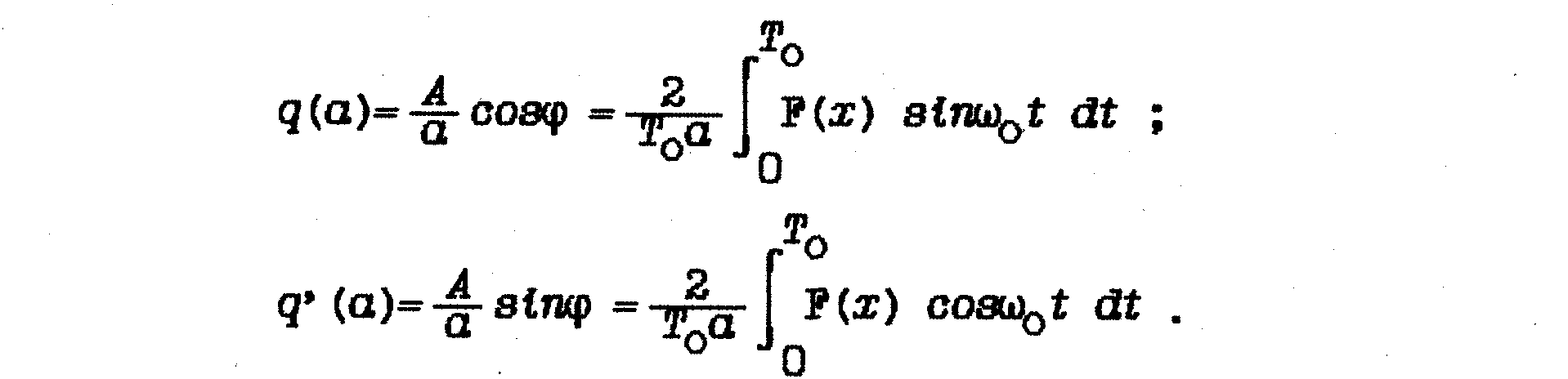
В табл.2 приведены коэффициенты гармонической линеаризации для типовых статических нелинейностей в случав симметричных колебаний на их входе.

Заметим, что дан однозначных нелинейностей. когда нелинейная характеристика элемента нечетна, т.е.

в разложении f{,x) в тригонометрический ряд содержатся лишь нечетные гармоники

причем сдвиги фаз _i равны нулю. Отсюда следует, что

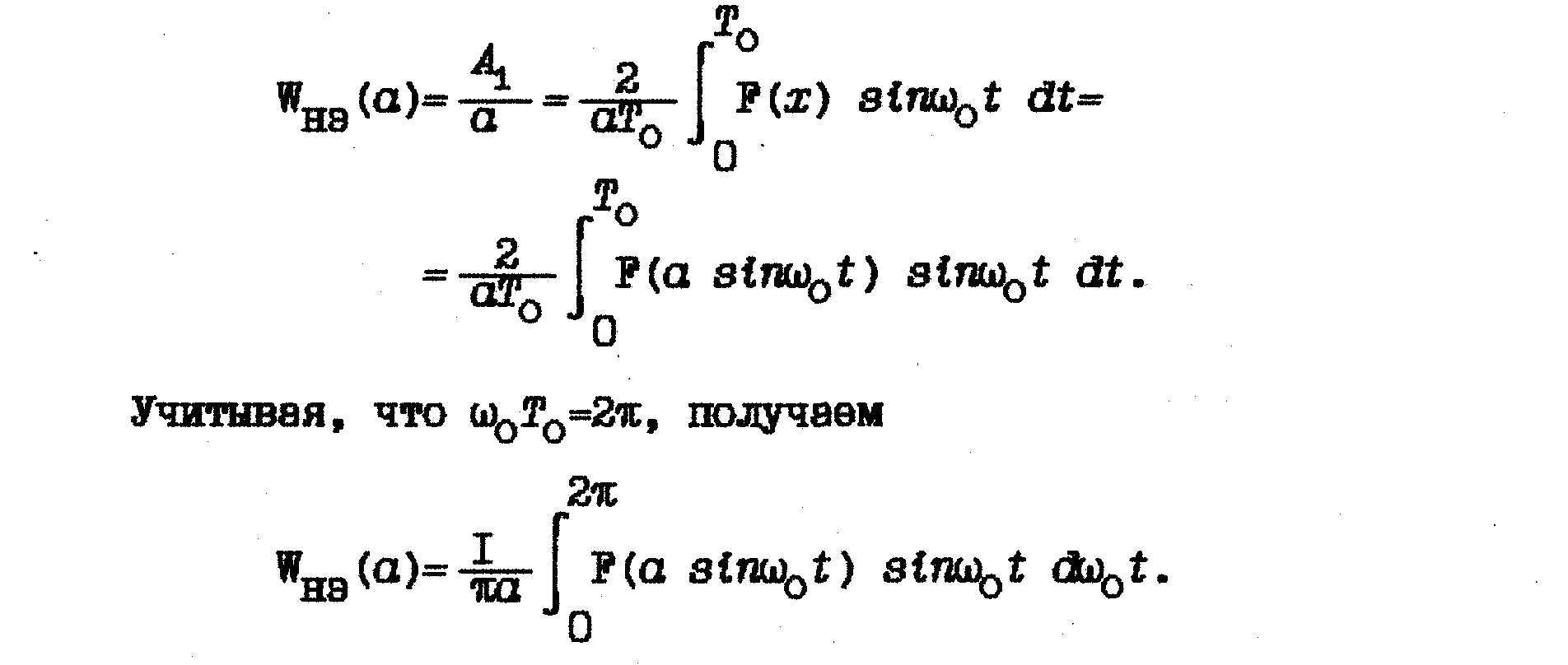
Таким образом, для однозначных статических нелинейностей коэффициент гармонической линеаризации q'()=0. Тогда

Проводя гармоническую линеаризацию для рассматриваемых типов нелинейных элементов, вместо исходной нелинейности получаем некоторую эквивалентную (в смысле прохождения первой гармоники) линейную характеристику, наклон которой зависит от амплитуды входного сигнала (рис.5 а, б).

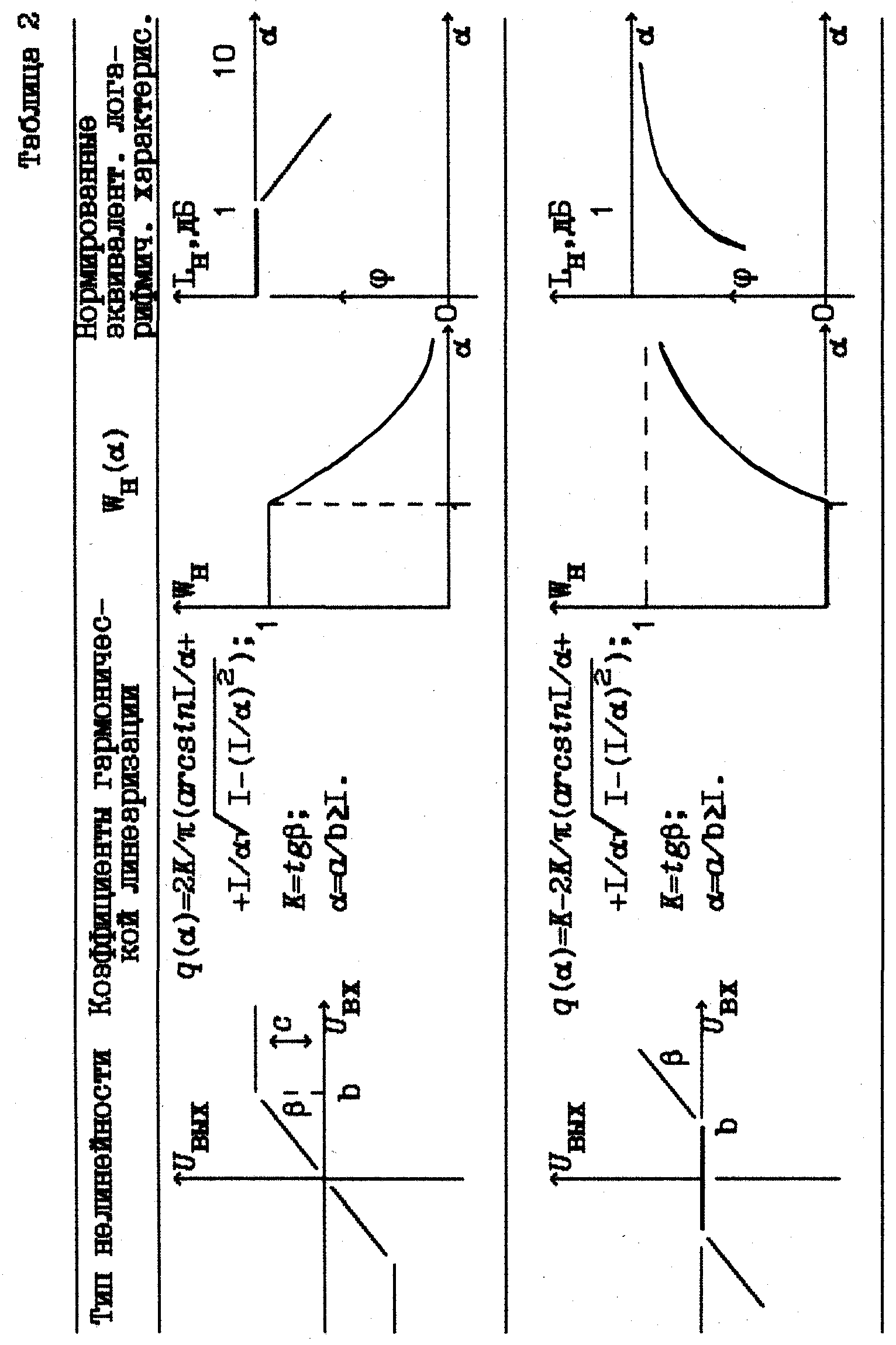
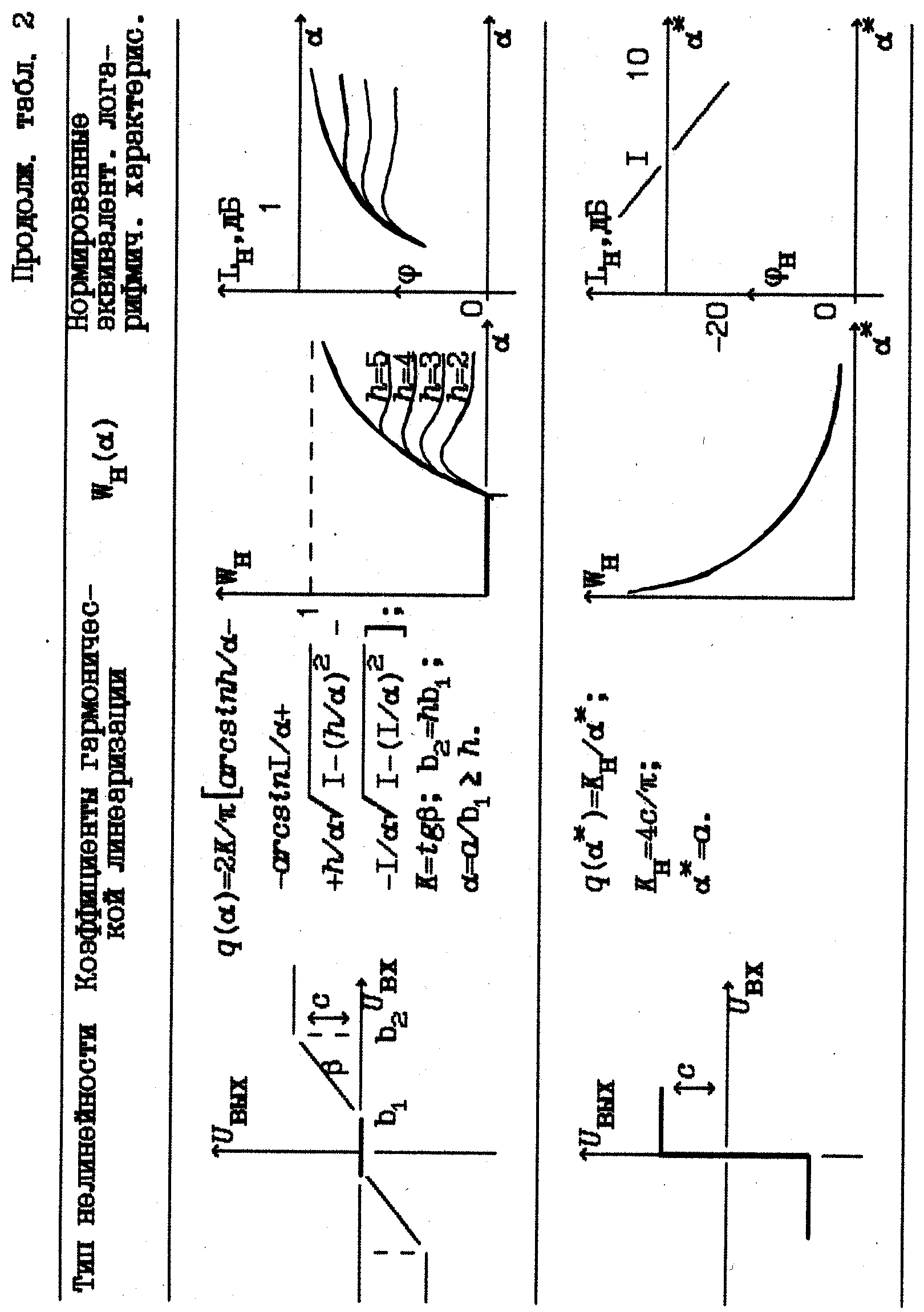
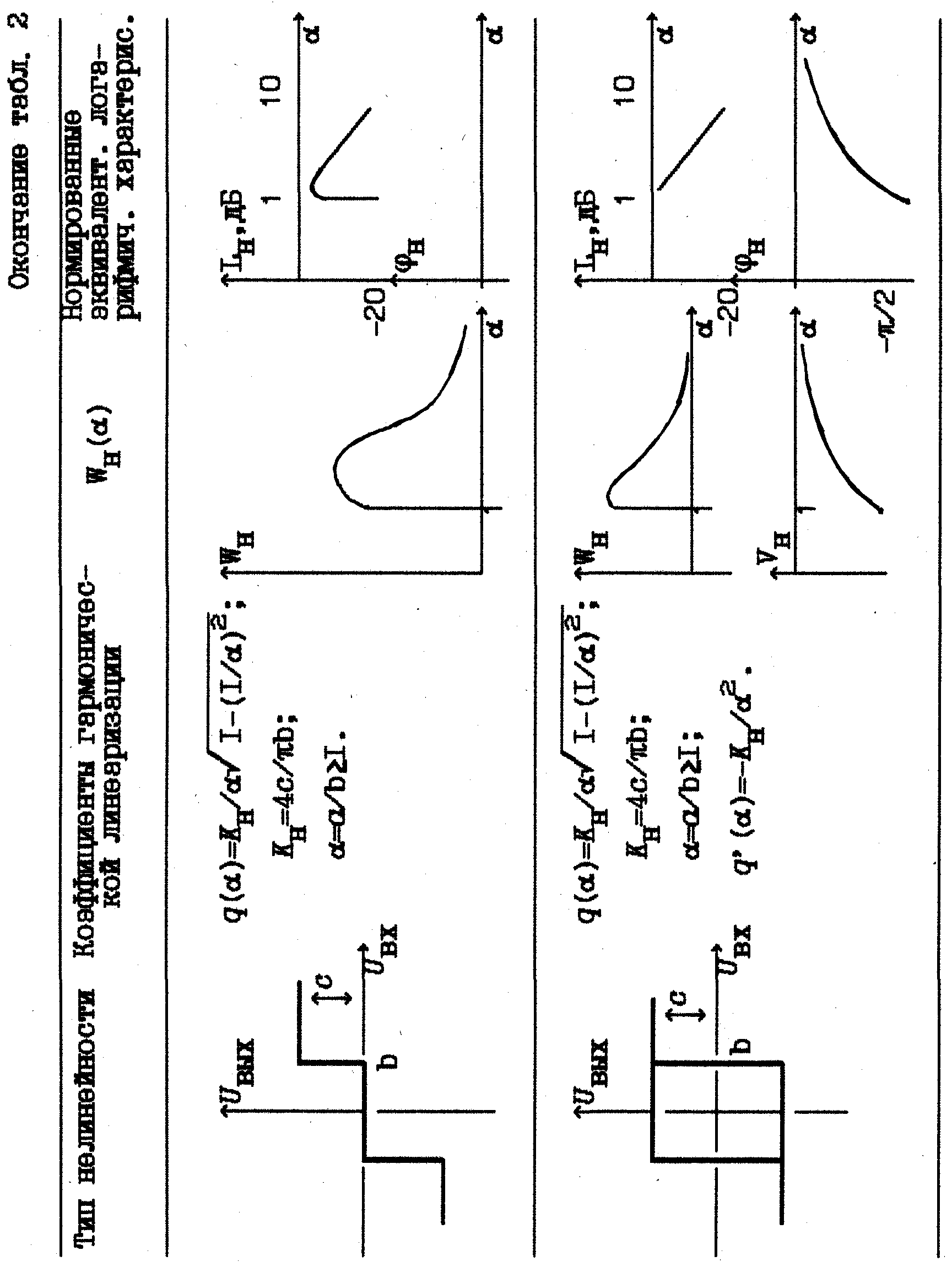
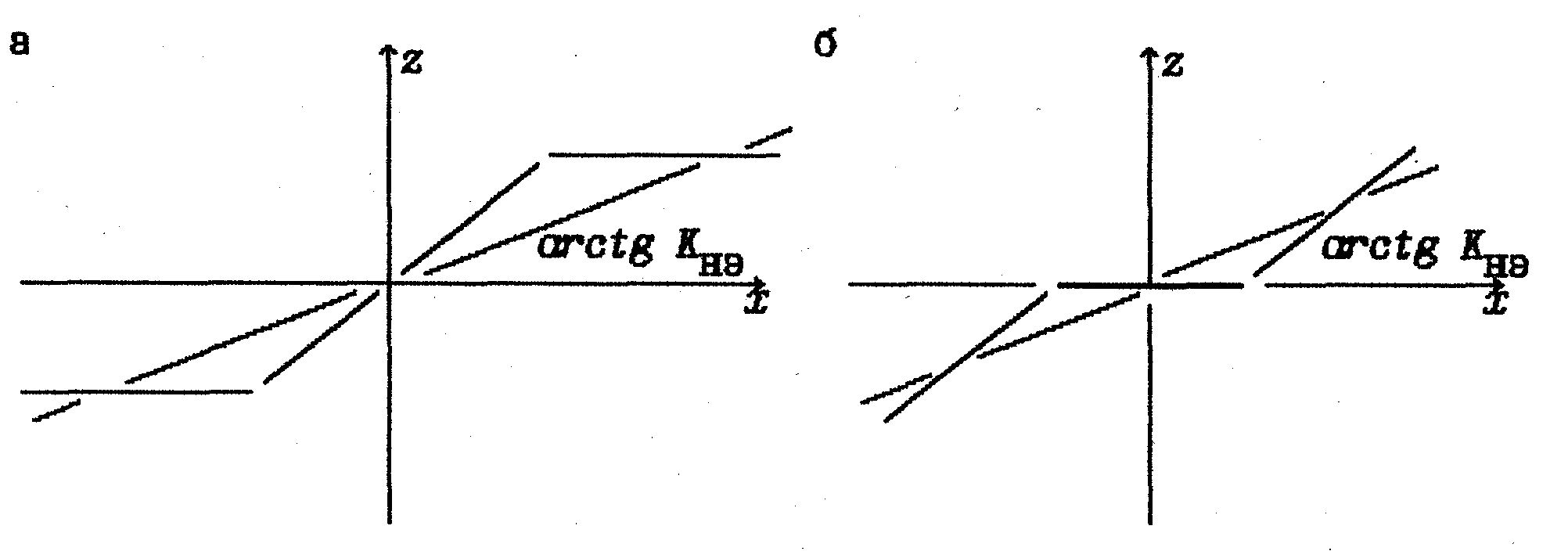
Рис. 5. Эквивалентные коэффициенты усиления нелинейных элементов типа "ограничение" (а) и "зона нечувствительности" (б)

ЭКВИВАЛЕНТНЫЕ АМПЛИТУДНО-ФАЗОЧАСТОТННЕ ХАРАКТЕРИСТИКИ ГАРМОНИЧЕСКИ ЛИНЕАРИЗОВАННЫХ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ

Частотная передаточная функция для статических нелинейных элементов в случае симметричных колебаний на их выходе в интервале отрицательных частот является комплексно-сопряженной с коэффициентом передачи в области положительных частот:

Поэтому достаточно проводить исследования нелинейных систем только для положительных частот.

Годограф W_НЭ() так же, как и в случае линейных систем, носит название амплитудно-фазовой характеристики (АФХ).

Запишем W_НЭ() в показательной форме:

где А () - модуль комплексного выражения W_НЭ(), называемый амплитудно-амплитудной характеристикой (ААХ);

() - фазоамплитудная характеристика (ФАХ).

ААХ и ФДХ определяются, как

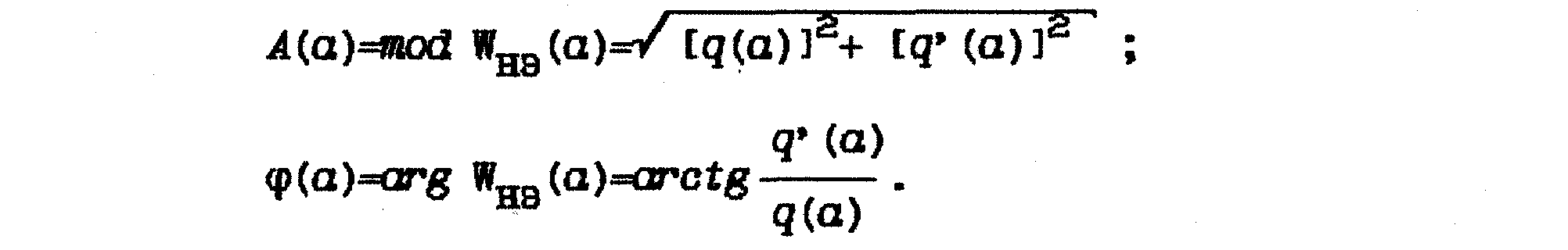
Заметим, что для нелинейных элементов с однозначной

Характеристикой

Для того чтобы можно было построить АФХ типовых нелинейных элементов, введем понятие эквивалентных нормированных амплитудных и фазовых характеристик в функции безразмерной (нормированной) амплитуда входного сигнала:

,

где b - один из параметров нелинейной характеристики (ширина зоны нечувствительности, ширина линейной зоны и т.д.).

Тогда

где q_Н() и g_Н^,() - приведенные нормированные коэффициенты гармонической линеаризации.

Соответствующие характеристики типовых нелинейных элементов приведены в табл. 2. Так, для нелинейностей типа "ограничение" и "зона нечувствительности" качественные характеристики g_н() имеют вид, показанный на рис. 6.

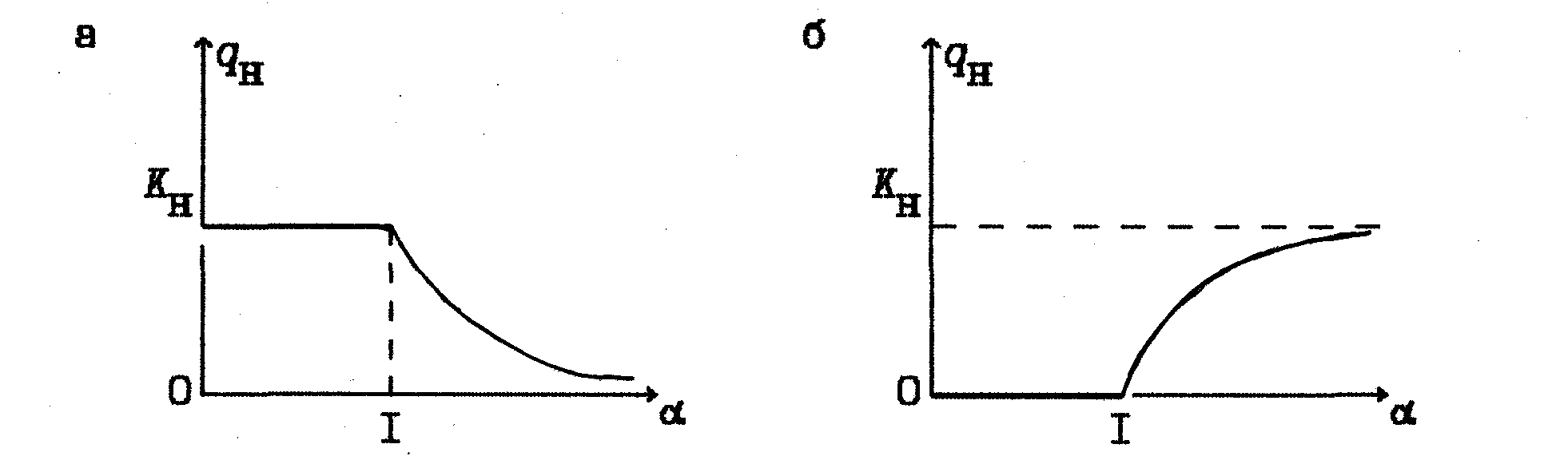
Рис. 6. График q_н() для нелинейностей типа "ограничение" (а) и "зона нечувствительности" (б)

По аналогии с логарифмическими характеристиками линейных звеньев можно ввести эквивалентные нормированные логарифмические амплитудные и фазовые характеристики нелинейных элементов

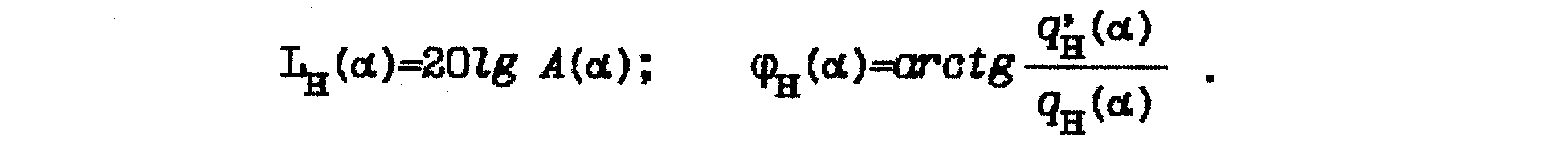
Эквивалентные логарифмические характеристики для типовых нелинейных элементов приведены в табл. 2.

В общем случае для сложных нелинейностей эквивалентная передаточная функция гармонически линеаризованного элемента имеет вид

АФХ в атом случае представляется семейством кривых, каждая из которых соответствует или постоянному значению частоты =const с изменяющейся амплитудой или, наоборот, =war, a =const.

УСЛОВИЯ БАЛАНСА АМПЛИТУД И ФАЗ

Предположим, что в замкнутой автономной системе, линейная часть которой является фильтром низких частот (рис. 2), имеются автоколебания. Тогда F(x)=W_нэ()x. Учитывая лишь первую гармонику на выходе линейной части, получаем колебание х частоты ₀:

Комплексные числа в левой и правой частях полученного равенства могут быть равны лишь при условии

Это выражение представляет собой необходимое условие существования автоколебаний в системе и называется условием гармонического баланса. Запишем это условие в показательной форме:

последнее уравнение справедливо, если

полученные равенства соответственно называют условиями баланса амплитуд и баланса фаз.

Таким образом, одно условие гармонического баланса, записанное для комплексных чисел, сводится к двум условиям -условиям баланса амплитуд и фаз, записанным для действительных чисел. Физический смысл баланса амплитуд сводится к следующему: во сколько раз одно из звеньев усиливает амплитуду колебаний, во столько же раз другое звено ее ослабляет. Условие баланса фаз сводится к тому, что общий фазовый сдвиг должен быть равен нулю либо целому числу, умноженному на 2.

Уравнения баланса амплитуд и фаз в общем случае являются нелинейными относительно  и ₀. Поэтому их решение удобно получать с помощью известных методов, например, методов Гольдфарба , Е.П.Попова, эквивалентных логарифмических частотных характеристик и т. п.

Однако для нелинейностей с однозначной характеристикой, когда z=F(x) - нечетная функция, коэффициент передачи нелинейного элемента W_нэ() оказывается действительной

величиной. При этом

_н()=0,

и тогда уравнение баланса фаз примет вид

_л(₀)=2m.

Это уравнение с одним неизвестным ₀, которое позволяет определить частоту автоколебаний. Из условия же баланса амплитуд можно найти амплитуду автоколебаний.

ОПРЕДЕЛЕНИЕ АМПЛИТУДЫ АВТОКОЛЕБАНИЙ

Нелинейная система, в которой происходят автоколебания. аналогична линейной системе, находящейся на границе устойчивости.

Для линейной системы, находящейся на границе устойчивости, также можно написать условия баланса амплитуд и фаз. Заменим нелинейный элемент линейным усилительным звеном с коэффициентом усиления к_пр, тогда условия баланса амплитуд и фаз примут вид

К_прА_Л(₀)=1 ;

_Л(₀)=2m .

Определяя из второго уравнения ₀, найдем предельный коэффициент усиления усилительного звена

Только при значении К равном К_пр в системе будут существовать незатухающие колебания, амплитуда которых определяется лишь начальными условиями. Однако в реальной системе неизбежны малые изменения величины К, и практически в линейной системе режим автоколебаний неосуществим.

В уравнении же баланса амплитуд нелинейного звена величина & не постоянна, а является функцией амплитуда автоколебаний  , что позволяет осуществить автоколебания в реальной нелинейной системе. Физический смысл К_пр_, состоит в том, что при замене нелинейного элемента линейным усилительным звеном величина К_пр является его предельным коэффициентом усиления, при котором замкнутая линейная система находится на границе устойчивости.

Поскольку К_пр может быть определен, исходя из параметров линейной части, то из уравнения баланса амплитуд

А_н()=К_пр

можно найти амплитуду автоколебаний ^* .

Нарисуем для примера А_н() нелинейных элементов типа "насыщение" и "зона нечувствительности" (рис.7).

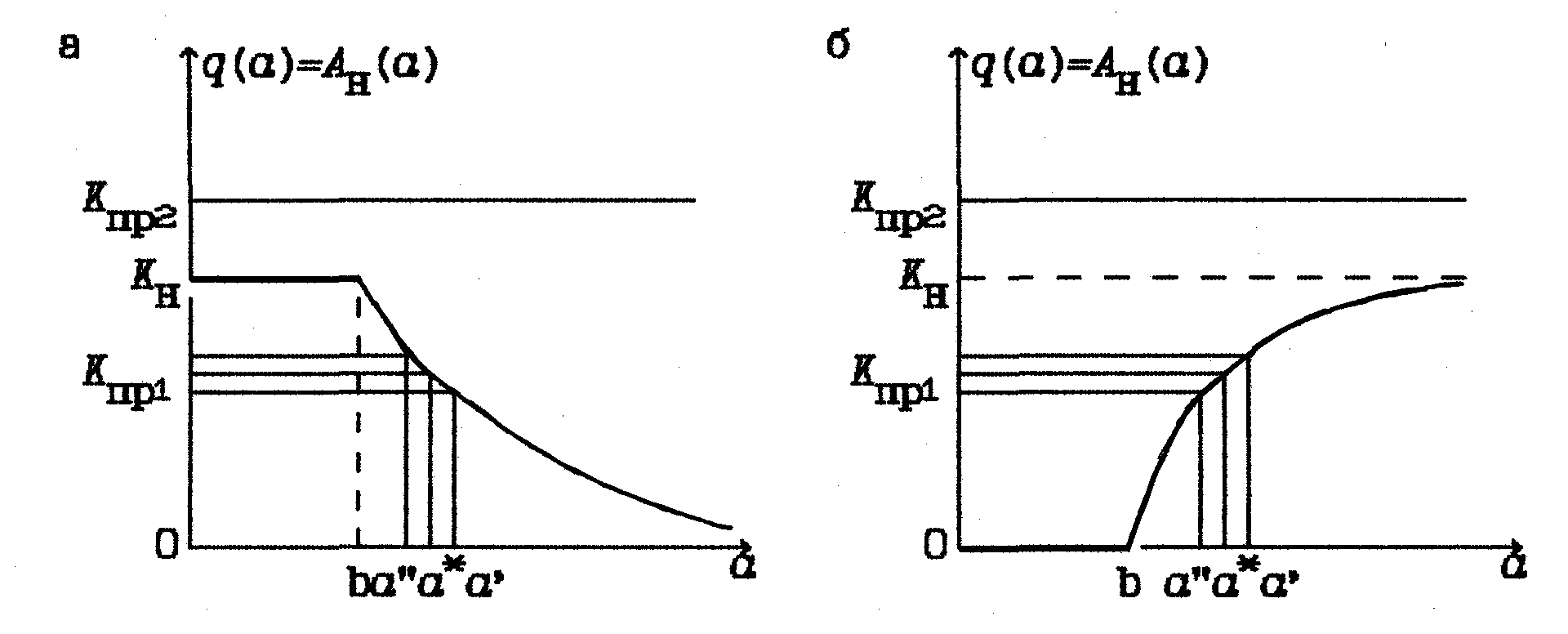
Рис. 7. Графическое определение амплитуда автоколебаний для нелинейных элементов типа "ограничение" (а) и "зона нечувствительности" (б)

Проведем на графиках рис. 7, а, б горизонтальную прямую с ординатой К_пр. Точка пересечения этой прямой с характеристикой А_н() позволяет определить искомую амплитуду автоколебаний. В случае, когда К_пр=К_пр2 , прямая не пересекает характеристики А_н() и, следовательно, автоколебаний нет и система устойчива.

Для существования автоколебаний в реальной системе необходимо, чтобы они были устойчивы.

Состояние равновесия для системы с характеристикой на рис. 7, а можно рассматривать как автоколебания с амплитудой ,

равной нулю. Соответствующий коэффициент передачи нелинейного элемента равен К_н, он больше, чем К_пр, т.е.

.

В результате каких-либо начальных условий в системе возникнут сколь угодно малые колебания, амплитуда которых начнет увеличиваться до тех пор, пока не дойдет до значения а*. Следовательно, положение равновесия системы неустойчиво, а устойчивым является лишь предельный цикл с амплитудой автоколебаний а*.

Во втором случае (рис. 7, б), если по каким-либо причинам амплитуда автоколебаний а уменьшится от значения а* до значения а", то коэффициент передачи К(а) становится меньше К_пр1. . Колебания начинают затухать и их амплитуда уменьшается до тех пор, пока не станет равной нулю в начале координат и в системе наступит равновесие. Таким образом, автоколебания при a=a* неустойчивы, состояние же равновесия, соответствующее началу координат, устойчиво.

Следовательно, система устойчива, но устойчива в "малом". Если же начальные условия в системе таковы, что в ней возникнут колебания амплитуды а*, больше, чем a^*, то они начнут возрастать и система не вернется к положению равновесия, т.е. будет неустойчива.

В случае, когда К_ПР>К_Н (например, К_ПР2), какова бы ни была амплитуда колебаний, они будут всегда затухать и область устойчивости расширяется. Система оказывается устойчивой в "большом".