
- •2. Экстремум ф-ции неск.Переменных. Необх.И дост.Условия экстремума ф-ции 2 перем.
- •9. Свойства определённых интегралов
- •5. Замена переменной. Интегрирование по частям
- •7.Интегрирование рацион. Выражений и простейших дробей.
- •10. Формула Ньютона-Лейбница (вывод)
- •11. Замена переменной и интегрирование по частям в опр.Интеграле
- •12.Площадь плоской фигуры. Объем тела вращения
- •14.Несобственные интегралы от неограниченных ф-ций
- •15. Диф. Уравн-ния (основные понятия)
- •17. Линейные ду 1-го порядка
- •18. Линейные ду 2-го порядка с постоянными коэф.
- •19. Понятие числового ряда и суммы ряда. Геометрическая прогрессия
- •21. Интегральный признак сходимости ряда с положительными членами
- •22. Признаки сравнения для положительных рядов. Признаки Даламбера и Коши.
- •23. Знакопеременные ряды. Абсолютная и условная сходимость
- •24. Знакочередующиеся ряды. Признак Лейбница.
- •25. Понятие степенного ряда, область сходимости степенного ряда, теорема Абеля
- •26. Ряды Тейлора и Маклорена
1.Ф-ция нескольк. Перем. Частн. Производные и полн. Диф-ал
Пусть
имеется n
переменных величин, и каждому набору
их значений
![]() из некоторого множества Х соответствует
одно вполне определенное значение
переменной величины Z,
тогда говорят, что задана ф-я
неск-ких переменных
из некоторого множества Х соответствует
одно вполне определенное значение
переменной величины Z,
тогда говорят, что задана ф-я
неск-ких переменных
![]() Переменные
Переменные
![]() называют независимыми переменными, или
аргументами. Z
– зависимая переменная. Множество X
– область определения. Наприм. Ax
+ By+Cz+D=0
называют независимыми переменными, или
аргументами. Z
– зависимая переменная. Множество X
– область определения. Наприм. Ax
+ By+Cz+D=0
В дальнейшем будем изучать функции 2 переменных. Большинство результатов, которые справедливы для функций 2 переменных, по аналогии переносятся на ф-ции многих переменных. Z=f(x,y)
Для функции 2 переменных обл. определения – либо вся координатная плоскость Оху, либо её часть.
В общем случае ф-ция 2 переменных представляет собой поверхность в 3-мерном пространстве.
а) Частная производная ф-ции нескольких переменных. б) Частный и полный дифференциалы.
а) рассмотрим на примере ф-ции 2х переменных
x=f(x,y), точка A(x0,y0)
z=f(x0+x, y0+y)-f(x0,y0) - полное приращение.
Частное приращение по х (по у):
Zх=f(x0+x, y)-f(x0, y0)
Zу=f(y0+y, x)-f(x0, y0)
Частной
производной ф-ции z=f(x,y)
по переменной х назыв. Передел отношения
частного приращения
![]() к приращению независимой переменной
к приращению независимой переменной
![]() х
при стремлении
х
к 0, если этот предел существует, т. Е.
х
при стремлении
х
к 0, если этот предел существует, т. Е.
z’x
=
![]()
![]() =
=
![]()
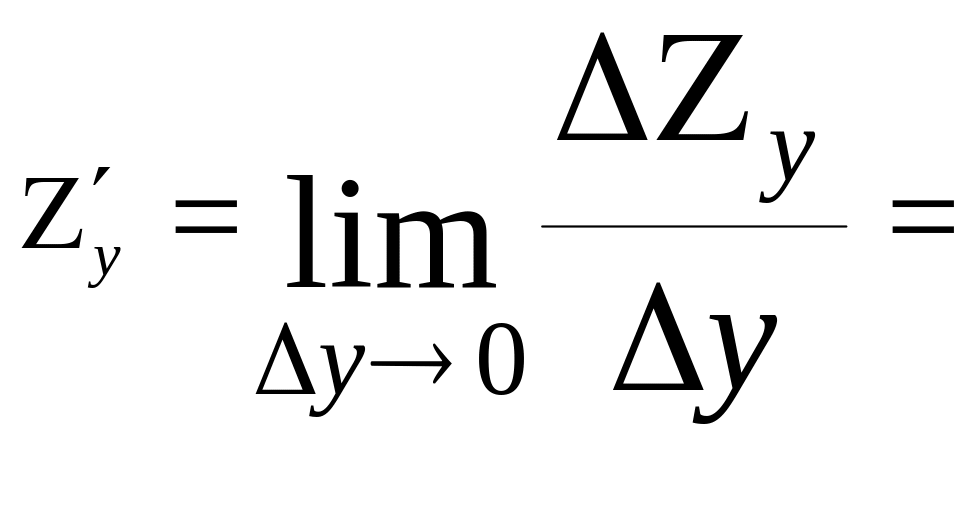
![]()
Частную производную функции 2-х переменных находят по тем же правилам, что и для функций одной переменной.
Отличие состоит в том, что при дифференциации функции по переменной х , у считается const, а при дифференцировании по у, х считается const.
Для ф-и 2-х переем-х сущ 4 части произв-х 2 порядка:
![]()
![]()
![]()
![]()
Б) Пусть z = f(x,y), тогда
dz
=
![]() - наз полным дифференциалом
- наз полным дифференциалом
Учитывая, что для ф-и f(x,y)=x, f(x,y)=y, df(x,y)=∆x=dx, df(x,y)=∆y=dy, полный диф-л можно записать в виде:
|
Чтобы найти полный дифференциал ф-ции надо найти частные производные от этой ф-ции по всем независимым переменным, умножить их на дифференциал этих переменных, рез-ты сложить.
Применим полный дифференциал к приближенным вычислениям. При достаточно малых по абсолютной величине х и y, приращение функции fdf. f(хо+х,yo+y) f(xо,yо)+ f ‘x(xo,yo)x+ f ‘y(xo,yo)y
2. Экстремум ф-ции неск.Переменных. Необх.И дост.Условия экстремума ф-ции 2 перем.
Локальный экстремум функции нескольких переменных. Необходимое и достаточное условие экстремума.
Точка Ро назыв. точкой локального max. и min., если сущ. такая окр. этой точки, что для всех точек Р из этой окр. отсеченных от самой Ро выполняется неравенство: f(Po)>f(P) или f(Po)<f(P). Точки max. и min. назыв. экстремумы, а значение в этих точках – экстрем. функции.
Необходимость существования экстремума: Если f(x,y) в точке Po(xо,yо) имеет экстремум и в этой точке существуют конечные частные производные, то они равны 0. ∂f / ∆x(x0,y0)=0
∂f /∆y=(x0,y0)=0 (система). Экстремумы функции f(x,y) надо искать в точках, координаты которые удовлетворяют системе уравнений. Из этой системы ищем стационарные точки. Достаточные условия существования эксремума функции 2-х переменных: Пусть точка Pо(xo,yo) – стационарная точка функции f(x,y). Введем следующие обозначения: Af”x(xo,yo), Bf”xy(xo,yo), Cf”y(xo,yo), AC-B2.Тогда, если: 1. >0 и при этом А>0 (C>0), то в точке Pо – минимум, если >0 и при этом А<0 (C<0), то в точке Pо – максимум. 2. Если <0, то в точке Pо экстремума нет. 3. Если =0, то требуется дополнительные исследования для увеличения и установки экстремума.
Условный экстремум функции нескольких переменных.
Задача нахождения экстремума ф-ции Z=f(x,y) при условии, что g(x,y)=0 (уравн-ние связи)
Простейший алгоритм решения этой задачи:
Из ур-ния связи выражаем у через х и подставляют в исходную ф-цию.Полученная ф-ция—одной переменной. И находят экстремумы этой ф-ции.
б) Метод множителей Лагранжа
Строим функцию
![]() -функция
3-х переменных
-функция
3-х переменных
Находим частные производные:
![]() Находим
точки экстремумов
Находим
точки экстремумов
![]()
Далее
- проверка достаточности условий для
функции 3-х переменных, строим опред-ль
3-го порядка из вторых произв-х в т.
![]() .
.
Глобальный экстремум функции нескольких переменных.
Пусть z=f(x,y) – диф.-ема на огран. замкнутом мн-ве D, по т. Вейерштрасса, на этом мн-ве, f принимает свои наиб. и наим. знач.-я, кот. назыв. Глоб экстремумом f.
. Интегрирование тригонометрических функций. J – знак интеграла
Интегралы вида J sinaxcosbxdx, J cosaxcosbxdx, Jsinaxsinbxdx, где a≠b, находятся с помощью формул:sinaxcosbxdx=1/2(sin(a-b)x+sin(a+b)x),cosaxcosbxdx=1/2(cos(a-b)x+cos(a+b)x), sinaxsinbxdx=1/2(cos(a-b)x-cos(a+b)x). Интегралы вида J R(sinx,cosx)dx, где R - рациональная функция, приводятся к интегрированию рациональных функций с помощью подстановки tgx/2=t, так как J R(sinxcosx)dx=2J R(2t/(1+t2),(1-t2)/(1+t2)) dt/(1+t2). Данная подстановка, являющаяся универсальной для интегралов этого типа, приводит иной раз к сложным выкладкам. В таких случаях используются более простые подстановки. Если выполнено рав-во R(-sinx,cosx)= - R(sinx,cosx) или R(sinx, - cosx)= - R(sinx,cosx), то применяют подстановку cosx=t либо sinx=t. Если выполнено рав-во R(-sinx,-cosx)=R(sinx,cosx), то интеграл приводят интегралу от рациональной дроби с помощью подстановки tgx=t, т.к. в этом случае R(sinx,cosx)=R(tgx), dx=dt/(1+t2)
3.М-д наим квадр-в. Выравн-е эмпирич данных по прямой
На практике часто приходится решать задачи сглаживанию эксперимент данных.
Пусть сущ завис-ть для 2-х переем-х, выраженная с пом таблицы, получ экспериментально
X
|
Y
|
Требуется наилуч образом сгладить эксперимент завис-ть м/д переем-ми х и у, т.е. установить зав-ть м/д х и у в виде формулы y = f(x).
О. Формулы, служ для аналитич представлений эксперимент данных, называются эмпирическими.
Задача нах-я эмпирич формул разбивается на 2 этапа.
I этап
Устанавливается вид зависимости y = f(x) (линейная, квадратичная, логарифмическая и т.д.).
II этап
Опред-ся неизв пар-ры этой ф-ии. Для этого применяют наиболее распр и теоретически обоснованный метод наименьших квадратов.
Он состоит в следующем:
В
кач-ве неизв пар-ра ф-и f(x)
выб-т такие знач-я, чтобы суммы кв-тов
невязок (![]() )
была мин. Невязка (
)
– это –откл-е от «теоретич» знач-й
)
была мин. Невязка (
)
– это –откл-е от «теоретич» знач-й
![]() ,
найд по эмпирич формулам y
= f(x)
от соответствующих опытных знач-й
.
,
найд по эмпирич формулам y
= f(x)
от соответствующих опытных знач-й
.
Рассм-м функцию
![]() (т.е.
сумму квадратов всех невязок)
(т.е.
сумму квадратов всех невязок)
Пусть
в кач-ве ф-и у = f(x)
взята лин ф-я у = ax
+ b.
Тогда задание сводится к отыскиванию
пар-ов a
и b,
при кот ф-я
![]() принимает
наим зн-е. Очевидно, что S
= S(a,b)
есть ф-я 2-х переем-х a
и b,
а
принимает
наим зн-е. Очевидно, что S
= S(a,b)
есть ф-я 2-х переем-х a
и b,
а
![]() и
и
![]() -
пост числа, полученные экспериментально.
-
пост числа, полученные экспериментально.
Т. о., достаточно исслед-ть ф-ю S = S(a,b) на экстремумы.
Находим частные производные
![]() или
или
![]()
![]()
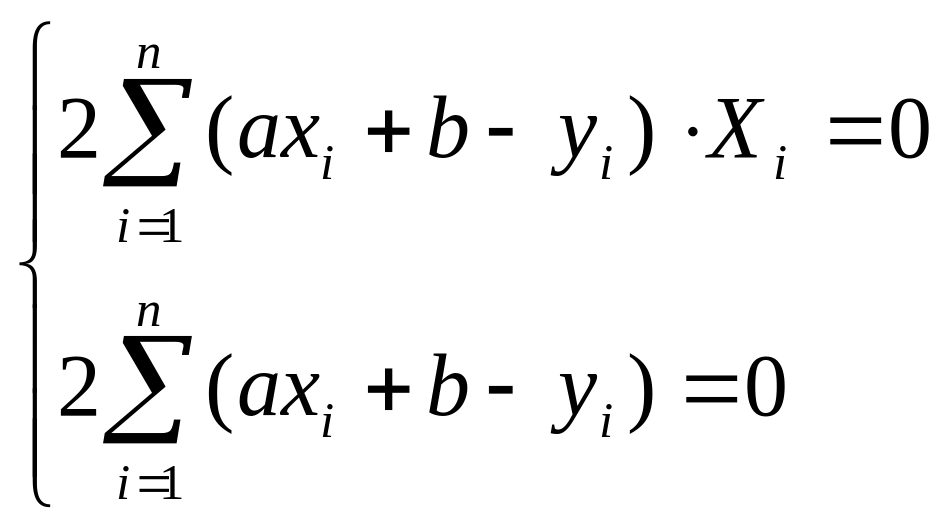
После преобразований, система принимает вид:
(**) 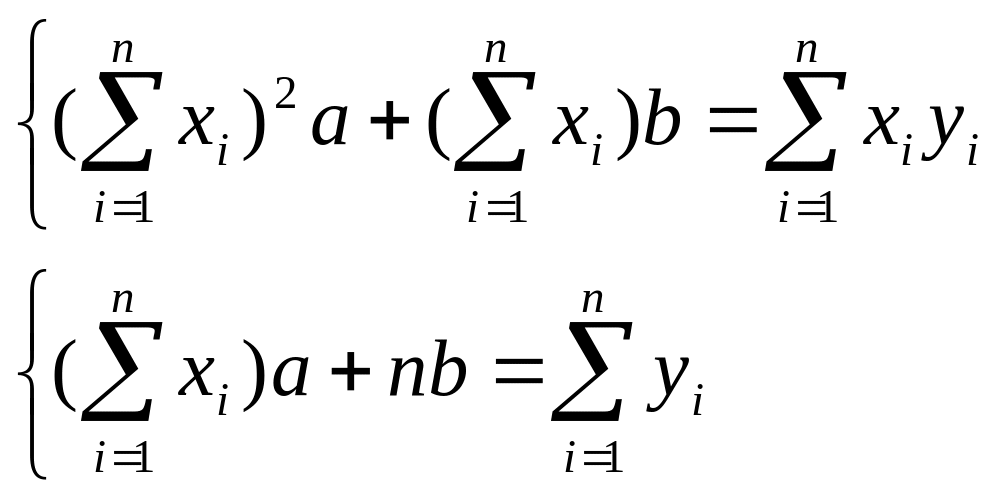 Система
(**) - система норм уравнений
Система
(**) - система норм уравнений
 т.к
квадрат ∑ >∑-мы квадратов
т.к
квадрат ∑ >∑-мы квадратов
![]()
Ф-я S = S(a,b) достигает своего min при a и b, найд из сист (**). Для этого проверим достаточные условия экстремума:
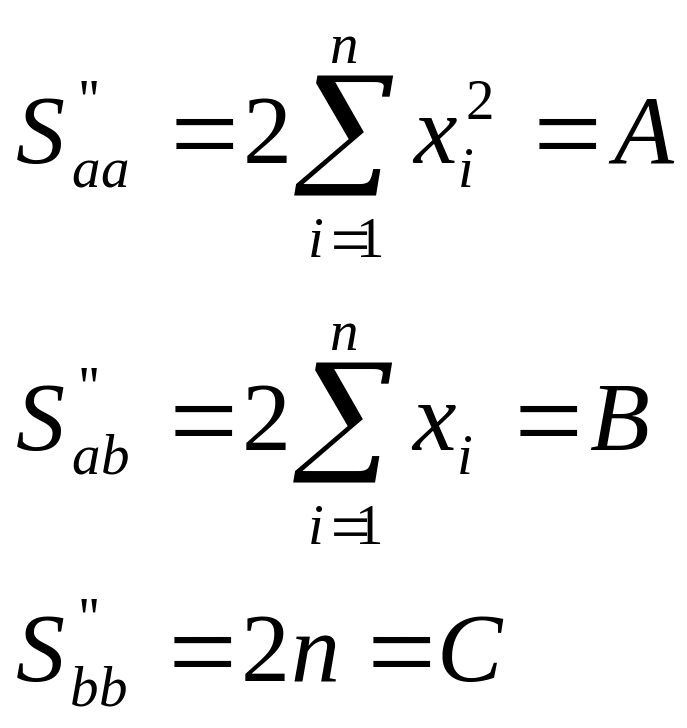
![]() функция
достигает min
(глобальный min).
функция
достигает min
(глобальный min).
4. Неопред интеграл, первообразная и их св-ва.
Пусть функции f(x) и F(x) определены на интервале (a;b). Если функция F(x) имеет производную на интервале (a;b) и для всех x € (a;b) выполняется равенство F’(x) = f(x), то функция F(x) называется первообразной функции f(x) на интервале (a;b).
Т.: Если F(x) первооб-я ф-и f(x), то F(x)+С тоже пер-я.
О. Мн-во всех перв-х ф-й F(x)+С для данной ф-и f(x) наз. неопред интегр ф-и f(x) обозн-ся
![]()
С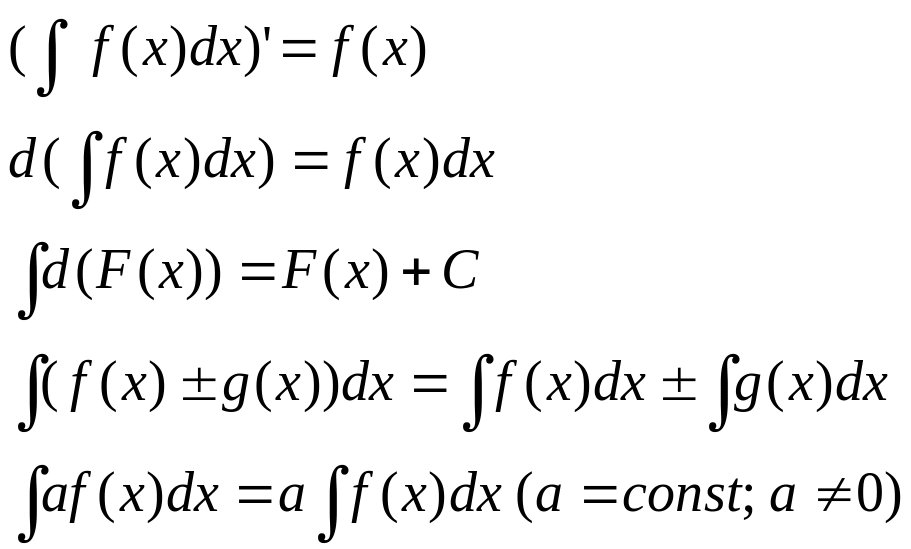 в-ва
НИ:
в-ва
НИ:
8.
Определение
и задачи, приводящие к понятию определенного
интеграла.
Пусть ф. у = f(х)
опр-на на отр. [а; b].
Разобьем отрезок [а; b]
на n
произвольн. частей точками а = x0<x1<x2<…<xn
= b.
Точки x0,
x1,
x2,…,xn
наз-ся
т-ми разбиения. В каждом из полученных
частичн. отр-в [xi-1;
xi]
выберем произв. образом точку ξ,
xi-1
≤
ξ
≤ xi.
Длину частичн. отр. обозначим ∆xi
=
xi
-
xi-1.
Сост-м сумму (1): σ
= f(ξ1)
∆x1
+
f(ξ2)
∆x2
+…+f(ξn)
∆xn
=![]() .
Сумма «сигма» назыв-ся интегральной
суммой для функции f(x)
на отрезке [a,
b]
соотв-щей данному разбиению отрезка
[a,
b]
на частичн. отр-ки и данному выбору точек
ξi.Обозначим
через λ
длину наибольшего отрезка разбиения.
.
Сумма «сигма» назыв-ся интегральной
суммой для функции f(x)
на отрезке [a,
b]
соотв-щей данному разбиению отрезка
[a,
b]
на частичн. отр-ки и данному выбору точек
ξi.Обозначим
через λ
длину наибольшего отрезка разбиения.![]()
Опр-е:
Если сущ-ет конечный независящий от
способа разбиения отрезка [a,
b]
на частичные отрезки и от выбора точек
ξi
соответствующих частичных отрезков
[xi-1;
xi]
предел интегральной суммы (1) при
![]() , то этот предел называется определенным
интегралом от функции f(x)
на пром-ке от a
до b
и обозн- ся
, то этот предел называется определенным
интегралом от функции f(x)
на пром-ке от a
до b
и обозн- ся
![]() (2)В
этом случае ф-ция называется интегрируемой
на отрезке [a,
b],
a
– нижний предел
(2)В
этом случае ф-ция называется интегрируемой
на отрезке [a,
b],
a
– нижний предел
