19. Бесконечно малые и бесконечно большие функции и их сравнение.

Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Примеры.

1. Функция f(x)=(x-1)² является бесконечно малой при x→1, так как 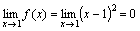(см. рис.).

2. Функция f(x) = tgx – бесконечно малая при x→0.

3. f(x) = ln (1+x)– бесконечно малая при x→0.

4. f(x) = 1/x– бесконечно малая при x→∞.

Установим следующее важное соотношение:

Теорема. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .

Обратно, если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Теорема 4 (свойства бесконечно малых функций).

1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

2. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая.

3. Произведение конечного числа бесконечно малых является бесконечно малой.

Сравнение ББ и БМ.

Бесконечно большие функции

Бесконечно малые функции

20.Непрерывность функции в точке – определение на языке ε – δ. Непрерывность функции в точке и односторонние пределы. Классификация разрывов.

Функция y=F(x) называется непрерывной в точке х=а, если предел в точке а существует и равен значению функции в этой точке

На языке y=F(x) непрерывна в точке х=а, если для любого положительного ε найдется положительное δ такое, что для всех х удовлетворяющих неравенству |x-a|< δ , выполняется неравенство |F(x)-F(a)|< ε. Н

Если оба односторонних предела существуют и равны F(a), то функция y=F(x) непрерывна в точке х=а.

Классификация точек разрыва: точки разрыва – точки, в которых функция не обладает свойством непрерывности.

-точка устраняемого разрыва: точка в которой существуют односторонние пределы, но функция не определена либо не совпадает по значению.

-точка разрыва 1 рода: точка в которой существуют оба односторонних предела, но они не совпадают.

-точка разрыва 2 рода: один из пределов не существует.

21.Свойства функции, непрерывных на отрезке. Теоремы о прохождении функции через 0 и о промежуточных значениях (Больцано- Коши). Теорема об ограниченности непрерывной на отрезке функции (Вейерштрасса) (без доказательства).

Теорема через 0: Если функция y=F(x) непрерывна на отрезке [a,b] и принимает на его концах значения равных знаков, то на интервале (a,b) существует точка ξ такая, что в ней функция обращается в нуль F(ξ)=0. Док-во: предположим что F(a)<0, F(b)>0. Рассмотрим множество тех x из отрезка [a,b] для которых F(x)<0; Обозначим это множество X : X={xЄ[a,b]:F(x)<0}. Множество ограничено сверху и имеет верхнюю грань, которую назовем ξ. Очевидно что ξ внутренняя точка отрезка. Пусть F(ξ)≠0, тогда существует интервал (ξ-δ, ξ+δ), в котором функция имеет определенный знак. Однако это невозможно, т.к. по определению точной верхней грани существует x из интервала (ξ-δ, ξ), где F(x)<0 и F(x)≥0 для всех x>ξ. Полученное противоречие доказывает что F(ξ)=0. Теорема доказана.

Теорема Больцано-Коши: Если функция y=F(x) непрерывна на отрезке [a,b], причем F(a)=A, F(b)=B и C – любое число между A и B, то на отрезке [a,b] найдется точка ξ такая, что F(ξ)=C. Док-во: В случаях A=B, C=A, C=B справедливость очевидна, т.к. ξ=a=b. Пусть A<C<B. Рассмотрим функцию F(x)=F(x)-C. На концах отрезка функция принимает значения разных знаков F(a)<0, F(b)>0, кроме того функция F(x) непрерывна на отрезке как разность двух непрерывных функций. Поэтому существует такая точка ξЄ(a,b), в которой F(ξ)=0, поэтому F(ξ)=C.

Теорема об ограниченности непрерывной на отрезке функции Вейерштрасса: Если функция непрерывна на отрезке, то она ограничена на нем.