2. Представление числовой информации

Системы исчисления

Система счисления – это способ представления чисел и соответствующие ему правила действия с числами.

Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.

В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает.

Примером непозиционной системы счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы:

I V L C D M

1 5 10 50 100 500 1000

П 1.11. Число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно 232.

В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются, например:

VI = 5 + 1 = 6, а IV = 5 – 1 = 4.

П 1.12. Записать римское число MCMXCVIII в десятичной системе

MCMXCVIII = 1000 + (- 100 + 1000) + (-10 +100) + 5 + 1 + 1+ 1 = 1998.

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием позиционной системы счисления.

Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Позиционный характер этой системы легко понять на примере любого многозначного числа. Например, в числе 333 первая тройка означает три сотни, вторая – три десятка, третья – три единицы.

Для записи чисел в позиционной системе с основанием n нужно иметь алфавит из n цифр. Обычно для этого при n < 10 используют n первых арабских цифр, а при n > 10 к десяти арабским цифрам добавляют буквы. Вот примеры алфавитов нескольких систем:

Основание	Название	Алфавит
n = 2	двоичная	0 1
n = 3	троичная	0 1 2
n = 8	восьмеричная	0 1 2 3 4 5 6 7
n = 16	шестнадцатеричная	0 1 2 3 4 5 6 7 8 9 A B C D E F

Если требуется указать основание системы, к которой относится число, то оно приписывается нижним индексом к этому числу. Например: 101101₂, 3671₈, 3В8F₁₆.

В системе счисления с основанием q (q-ичная система счисления) единицами разрядов служат последовательные степени числа q. q единиц какого-либо разряда образуют единицу следующего разряда. Для записи числа в q-ичной системе счисления требуется q различных знаков (цифр), изображающих числа 0, 1, …, q – 1. Запись числа q в q-ичной системе счисления имеет вид 10. Развернутой формой записи числа называется запись в виде

Здесь A_q –само число, q – основание системы счисления, a_i – цифры данной системы счисления, n – число разрядов целой части числа, m – число разрядов

дробной части числа.

Свернутой формой записи числа называется запись в виде

которой пользуются в повседневной жизни.

П 1.13. Записать в развернутом виде число А₁₀ = 4718,63

А₁₀ = 4*10³ + 7*10² + 1*10¹ + 8*10⁰ + 6*10^-1 + 3*10^-2 .

П 1.14. Записать в развернутом виде число А₈ = 7764,1

А₈ = 7*8³ + 7*8² + 6*8¹ + 4*8⁰ + 1*8^-1 .

П 1.15. Записать в развернутом виде число А₁₆ = 3АF

А₁₆ = 3*16³ + 10*16¹ + 15*16⁰ .

П 1.16. Все числа 112₃, 101101₂, 15FC₁₆, 101,11₂ перевести в десятичную систему

112₃ = 1*3² + 1*3¹ + 2*3⁰ = 9 + 3 + 2 = 14₁₀,

101101₂ = 1*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 32 + 8 + 4 + 1 = 45₁₀,

15FC₁₆ = 1*16³ + 5*16² + 15*16¹ + 12 = 4096 + 1280 + 240 + 12 = 5628₁₀,

101,11₂ = 1*2² + 0*2¹ + 1*2⁰ + 1*2^-1 + 1*2^-2 = 4 + 1 + ½ + ¼ = 5 + 0,5 + 0, 25 = 5,75₁₀.

П 1.17. У жителей села «Не десятичное» на ферме имеется 120 голов рогатого скота, из них 53 коровы и 34 быка. Какая система счисления используется сельчанами?

Решение: Самая большая цифра в рассматриваемых числах – это цифра 5. Значит, она входит в состав алфавита искомой системы счисления. Тогда основание системы счисления больше 5. Задачу можно решить методом подстановки оснований 6 и 7 или математически.

Примем за х основание искомой системы счисления. Тогда после перевода чисел, стоящих в правой и левой частях, в десятичную систему счисления получим следующее равенство: х² + 2х = 5х + 3 + 3х + 4. После преобразований получим уравнение х² – 6х – 7 = 0.

Ответ х = 7.

Перевод десятичных чисел в другие системы счисления

1. Последовательно выполнить деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получите неполное частное, меньшее делителя;

2. полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;

3. составить число в новой системе счисления, записывая его, начиная с последнего частного.

П 1.18. Перевести число 37₁₀ в двоичную систему счисления. Для обозначения цифр в записи числа используем символику: а₅ а₄ а₃ а₂ а₁ а₀.

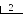
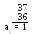
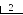
Отсюда 37₁₀ = 100101₂.

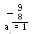
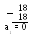
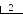
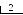
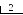
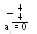
1 = а₅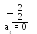

П 1.19. Перевести десятичное число 315 в восьмеричную и в шестнадцатеричную системы счисления:

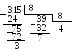
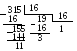
Отсюда следует: 315₁₀ = 473₈ = 13В₁₆.

Напомним, что 11₁₀ = В₁₆.

Перевод двоичных чисел в системы счисления с основанием 2ⁿ

Для того, чтобы целое двоичное число записать в системе счисления с основанием q = 2ⁿ (4, 8, 16 и т.д.), нужно:

1. данное двоичное число разбить справа налево на группы по n цифр в каждой группе;

2. если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов;

3. рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q = 2ⁿ.

Ниже приводится таблица с числами систем счисления с основаниями q = 2ⁿ, где n = 1, 3, 4 и десятичной системы счисления.

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	А
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

П 1.20. Перевести число 1100101001101010111₂ в восьмеричную систему счисления.

Разбиваем число на группы по три цифры – триады (т.к. q = 8, 8 = 2ⁿ, n = 3) справа налево и, пользуясь таблицей, записываем соответствующее восьмеричное число.

001	100	101	001	101	010	111
1	4	5	1	5	2	7

Ответ: 1451527₈

П 1.21. Перевести число 1100101001101010111₂ в шестнадцатеричную систему счисления.

Разбиваем число на группы по четыре цифры – тетрады (т.к. q = 16, 16 = 2ⁿ, n = 4) справа налево и, пользуясь таблицей, записываем соответствующее шестнадцатеричное число.

0110	0101	0011	0101	0111
6	5	3	5	7

Ответ: 65357₁₆

П 1.22. Чему равно значение основания системы счисления Х, если известно, что 175_Х = 7D₁₆?

Решение: Запишем числа 175_Х и 7D₁₆ в десятичной системе счисления.

175_Х = Х ² + 7Х + 5,

7D₁₆ = 7·16 + 13 = 125.

Но так как эти числа равны, то Х ² + 7Х + 5 = 125.

Корни полученного квадратного уравнения: Х = 8 и Х = -15 (не подходит, так как основание системы счисления не может быть отрицательной величиной). Следовательно, основание системы счисления – 8.

Для того, чтобы произвольное число, записанное в системе счисления с основанием q = 2ⁿ, перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-разрядным эквивалентом в двоичной системе счисления.

Применительно к компьютерной информации часто используются системы с основанием 8 (восьмеричная) или 16 (шестнадцатеричная).

П 1.23. Перевести двоичное число 110111101011101111 в шестнадцатеричную систему счисления.

Решение: Разделим данное число на группы по четыре цифры, начиная справа. Если в крайней левой группе окажется меньше четырех цифр, то дополним ее нулями

0011 0111 1010 1110 1111.

А теперь, глядя на двоично-шестнадцатеричную таблицу, заменим каждую двоичную группу на соответствующую шестнадцатеричную цифру

3 7 А Е F.

Следовательно

110111101011101111₂ = 37AEF₁₆.

Тестовые задачи

Т 1.21. В саду 100_q плодовых кустарников, из них 33 куста малины, 22 куста смородины красной, 16 кустов черной смородины и 17 кустов крыжовника. В какой системе счисления подсчитаны деревья?

Варианты ответа: а) 7; б) 9; в) 11; г) 13.

Т 1.22. Было 53_q груши. После того, как каждую из них разрезали пополам, стало 136 половинок. В системе счисления с каким основанием вели счет?

Варианты ответа: а) 11; б) 13; в) 15; г) 17.

Т 1.23. Какое число больше?

Варианты ответа: а) 152₇; б) 152₁₀; в) 152₁₂; г) 152₁₆.

Т 1.24. Переведите двоичные числа в восьмеричную систему счисления:

а) 110000110101; 1010101 б) 11100001011001; 1000010101.

Т 1.25. Переведите двоичные числа в шестнадцатеричную систему счисления: а) 11011010001; 111111111000001 б) 10001111010; 100011111011.

Т 1.26. Переведите шестнадцатеричные числа в двоичную систему счисления: а) 1АС7 б) FACC.

Т 1.27. Переведите числа из восьмеричной системы счисления в шестнадцатеричную: а) 774; б) 665.