
- •7.1. Інтегральна сума. Визначений інтеграл як границя інтегральної суми.
- •7.2. Властивості визначених інтегралів.
- •7.3. Формула Ньютона-Лейбніца.
- •7.4. Методи обчислення визначених інтегралів.
- •7.4.2 Інтегрування частинами.
- •7.4.3 Наближене обчислення визначених інтегралів.
- •7.5. Невласні інтеграли.
- •7.5.1. Невласні інтеграли з нескінченною границею.
- •7.5.3. Невласні інтеграли від необмежених функцій.
Т е м а 7. ВИЗНАЧЕНИЙ ІНТЕГРАЛ
Поняття визначеного інтеграла відіграє важливу роль у математичному аналізі та у різноманітних його застосуваннях.
7.1. Інтегральна сума. Визначений інтеграл як границя інтегральної суми.
Нехай
на відрізку
![]() задана обмежена функція
задана обмежена функція
![]() .
Розіб’ємо точками
.
Розіб’ємо точками
![]() ,
,
![]() ,
,
![]() ,
,
![]() (
(![]() )
цей відрізок на
)
цей відрізок на
![]() частин:
частин:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
(
,
(![]() ,
,
![]() ),
),
оберемо
довільно у кожній з них точку
![]() (
(![]() )
і обчислимо значення
)
і обчислимо значення
![]() у точках
у точках
![]() .
Позначимо довжину відрізка
.
Позначимо довжину відрізка
![]() через
через
![]() (
(![]() )
і складемо суму
)
і складемо суму
![]() .
Діаметром розподілу називають величину
.
Діаметром розподілу називають величину
![]() .
Зрозуміло, що з
.
Зрозуміло, що з
![]() витікає
витікає
![]() .
(Чи є вірним зворотне твердження?).
.
(Чи є вірним зворотне твердження?).
Зверніть
увагу на зв’язок інтегральної суми з
визначеним інтегралом: границю
інтегральної суми при
![]() ,
якщо вона не залежить від способу поділу
відрізка
,
якщо вона не залежить від способу поділу
відрізка
![]() та вибору точок
та вибору точок
![]() ,
називають визначеним інтегралом від
функції
,
називають визначеним інтегралом від
функції
![]() за проміжком
за проміжком
![]() і позначають символом
і позначають символом
![]() .
.
Отже,
![]() .
(7.1)
.
(7.1)
Якщо
до функції
![]() існує інтеграл (7.1), то вона називається
інтегровною на відрізку
існує інтеграл (7.1), то вона називається
інтегровною на відрізку
![]() .
Числа
.
Числа
![]() і
і
![]() мають назву відповідно
нижньої та верхньої границь інтеграла.
мають назву відповідно
нижньої та верхньої границь інтеграла.
При
![]() інтегральна сума припускає просте
геометричне тлумачення: вона
чисельно дорівнює площі ступінчастої
фігури, складеної з окремих прямокутників
(рис. 7.1) шириною
інтегральна сума припускає просте
геометричне тлумачення: вона
чисельно дорівнює площі ступінчастої
фігури, складеної з окремих прямокутників
(рис. 7.1) шириною
![]() та висотою
та висотою
![]() .
.
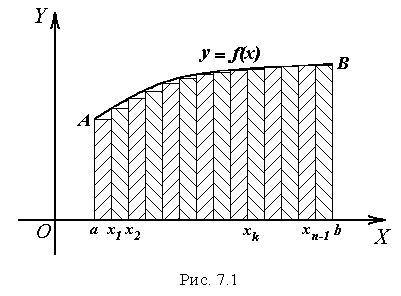
Інтуїтивно
ясно (і це можна довести), що площа
криволінійної трапеції, обмеженої
кривою
![]() і прямими
і прямими
![]() ,
,
![]() ,
,
![]() (див. рис. 7.1), дорівнює інтегралу (7.1).
(див. рис. 7.1), дорівнює інтегралу (7.1).
Якщо
функція
![]() ,
то інтегралу (7.1) можна приписати значення
площі криволінійної трапеції, розташованої
нижче осі
,
то інтегралу (7.1) можна приписати значення
площі криволінійної трапеції, розташованої
нижче осі
![]() ,
зі знаком мінус (за означенням, вважаємо
площу додатковою величиною). Для
знакозмінної функції
,
зі знаком мінус (за означенням, вважаємо
площу додатковою величиною). Для
знакозмінної функції
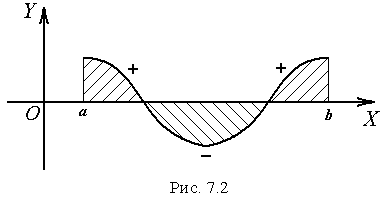
![]() (рис. 7.2) інтеграл (7.1) геометрично являє
собою алгебраїчну суму площ фігур,
причому площі фігур, розташованих вище
осі
(рис. 7.2) інтеграл (7.1) геометрично являє
собою алгебраїчну суму площ фігур,
причому площі фігур, розташованих вище
осі
![]() ,
входять зі знаком плюс, а площі фігур,
розташовані нижче осі
,
входять зі знаком плюс, а площі фігур,
розташовані нижче осі
![]()
зі знаком мінус.
зі знаком мінус.
Значення
деяких інтегралів можна одержати
безпосередньо з геометричних міркувань.
Так, якщо
![]() стала в
інтервалі
стала в
інтервалі
![]() (
(![]() ),
то маємо
),
то маємо
![]() .
.
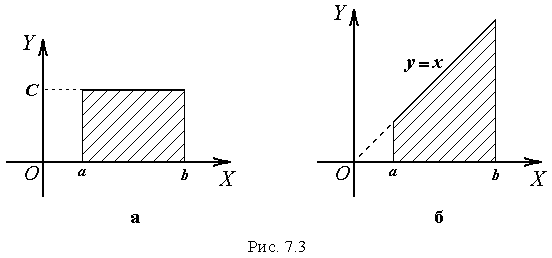
Даний
інтеграл дорівнює площі (рис. 7.3а)
прямокутника висотою
![]() і шириною
і шириною
![]() .
.
Якщо
![]() ,
то інтеграл
визначається
формулою
,
то інтеграл
визначається
формулою
![]() .
.
і дорівнює площі трапеції (див. рис. 7.3б).
Л і т е р а т у р а: [4, гл. 6, §4, п. 1; 5, гл. 6, §6.1; 6, гл. ХI, §1,2].
7.2. Властивості визначених інтегралів.
Перелічені нижче властивості інтегралів є безпосереднім висновком означення інтеграла як границі інтегральної суми. Треба звернути увагу на застосування цих властивостей.
-
Якщо поміняти місцями верхню і нижню границі інтеграла, знак інтеграла змінюється на протилежний:
![]() .
.
-
Якщо верхня і нижня границі інтеграла рівні між собою, то інтеграл обертається в нуль:
![]() .
(7.2)
.
(7.2)
-
Визначений інтеграл адитивний відносно інтервала інтегрування:
![]() ,
(7.3)
,
(7.3)
якщо
![]() .
.
-
Визначений інтеграл задавольняє умові лінійності:
![]() .
.
-
Якщо в проміжку
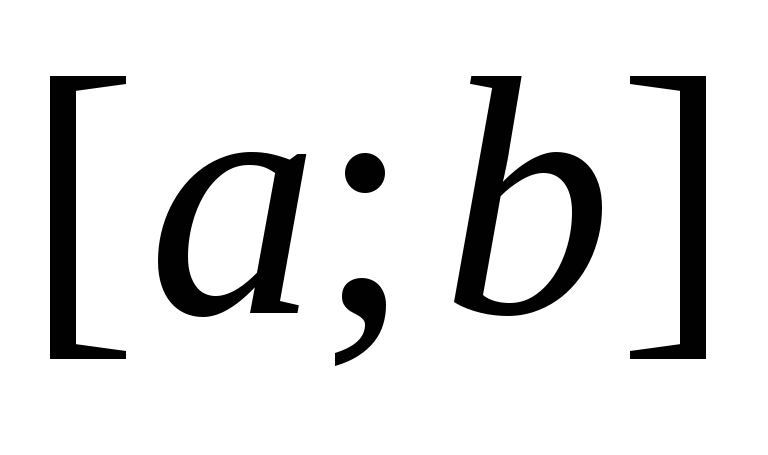 функції
функції
 і
і
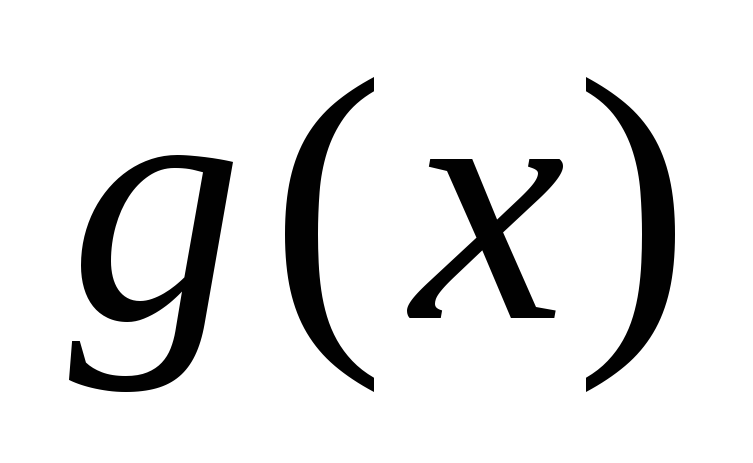 інтегровні і задавольняють умові
інтегровні і задавольняють умові
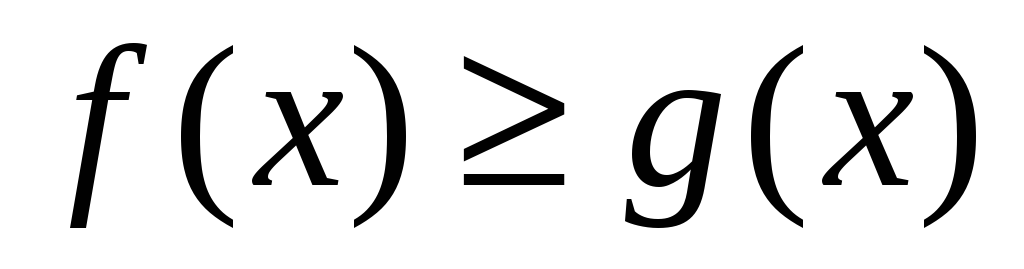 ,
то:
,
то:
![]() ,
,
при
![]() .
.
-
Якщо інтегровна в проміжку
 функція
функція
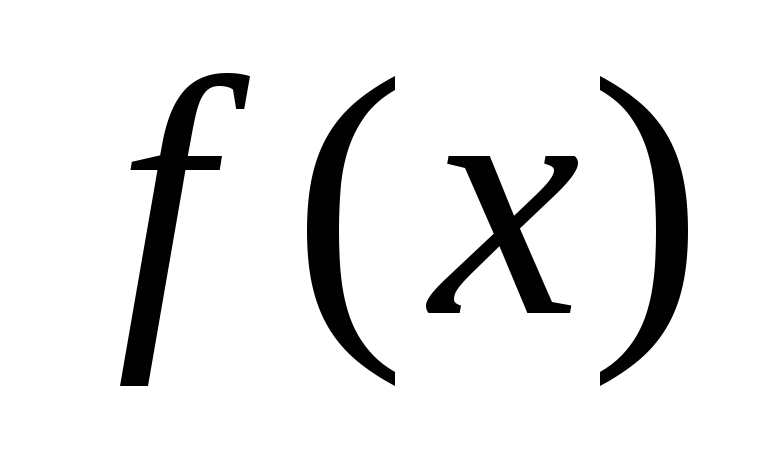 задавольняє рівності
задавольняє рівності
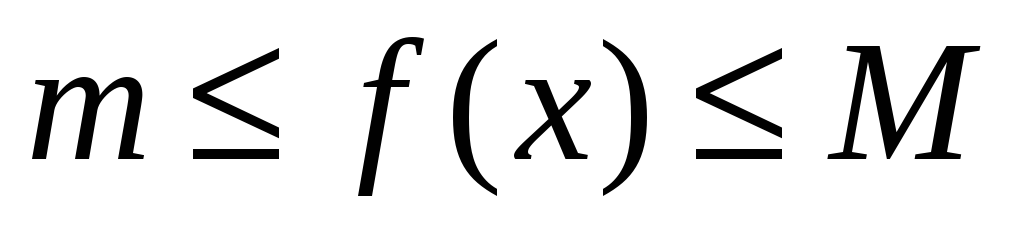 ,
то:
,
то:
![]() .
.
при
![]() .
.
-
Теорема про середнє значення. Якщо функція
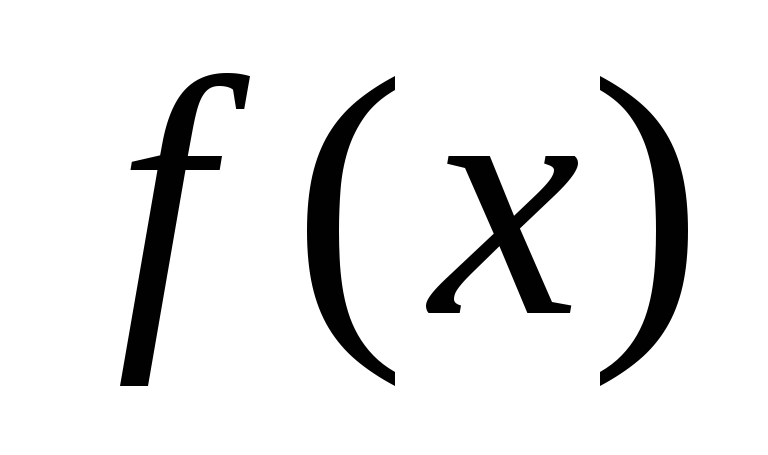 неперервна в проміжку
неперервна в проміжку
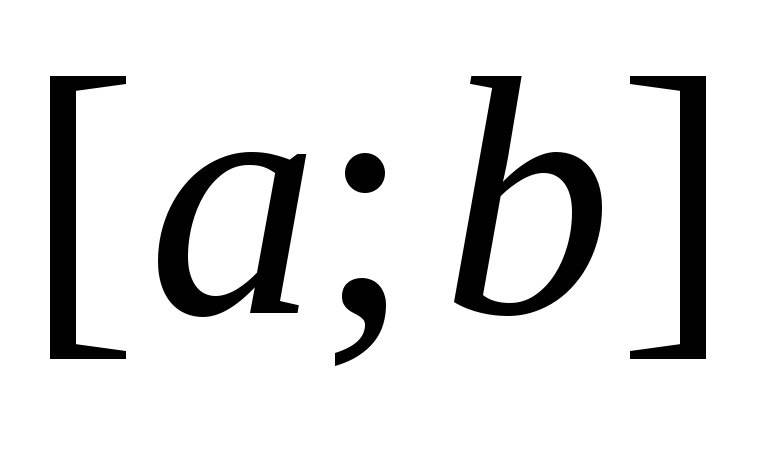 ,
тоді існує така точка
,
тоді існує така точка
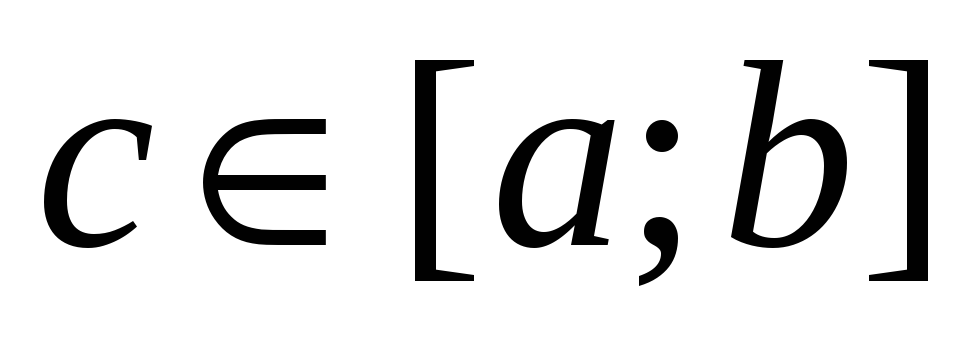 ,
що:
,
що:
![]() .
(7.4).
.
(7.4).
-
Узагальнена теорема про середнє значення. Якщо функція
 неперервна, а функція
неперервна, а функція
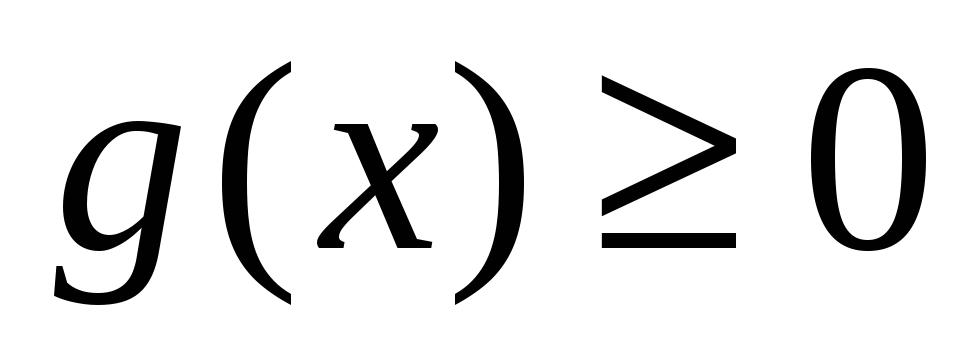 інтегровна в проміжку
інтегровна в проміжку
 ,
тоді існує така точка
,
тоді існує така точка
 ,
що:
,
що:
![]() .
.
Л і т е р а т у р а: [4, гл. 6, §4, п. 3; 5, гл. 6, §6.2; 6, гл. ХI, §3].
