Краткая теория

Передаточная функция распределенного пропорционально-интегрирующего блока может быть записана в виде:

, ,

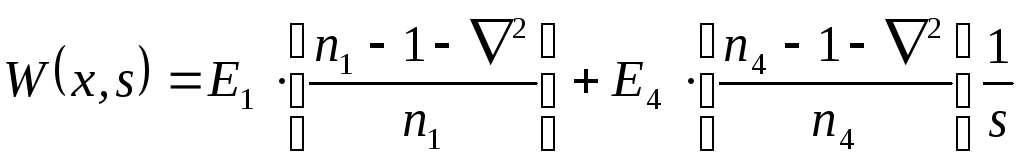оператор Лапласа.

Неизвестными параметрами здесь являются и . Для определения параметров E₁, n₁ решим систему уравнений:

,

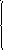
(6.1)

,

где , – коэффициенты усиления (определяются из графиков ЛАЧХ и ФЧХ).

Для нахождения n4 (весовой коэффициент), решим следующую систему уравнений:

,

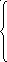
(6.2)

,

где , – значения круговой частоты (определяются из графиков ЛАЧХ и ФЧХ).

Далее, строим реальную частотную характеристику регулятора (см. рис. 6.1).

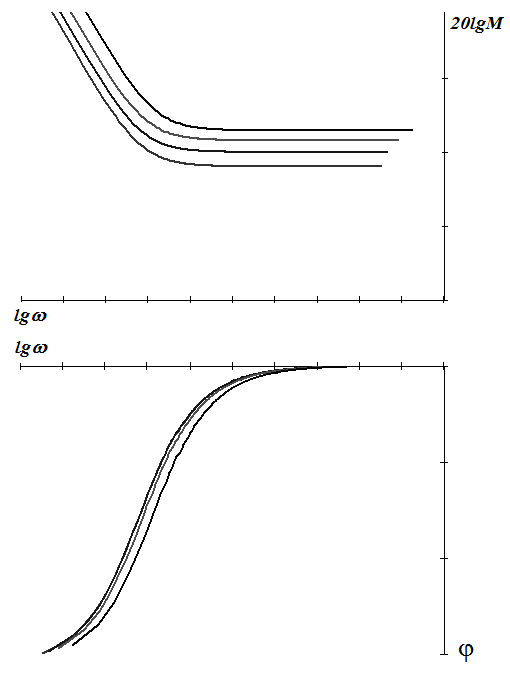
Рис. 6.1. Пример ЛАФЧХ распределенного ПИ-регулятора.

Лабораторная работа №7 Моделирование распределенных систем с векторным входным воздействием

ЦЕЛЬ РАБОТЫ:

Составление математической и численной модели распределенного объекта и проведение экспериментов.

ЗАДАНИЯ НА ПРАКТИЧЕСКУЮ РАБОТУ:

1. Составить математическую модель распределенного объекта управления;

2. Составить численную модель распределенного объекта управления.

3. Подавая на вход распределенного объекта распределенное воздействие, выбранное в соответствии с граничными условиями, получить функции выхода объекта: графики переходных процессов в точке указанной преподавателем; графики зависимостей входного воздействия и функции выхода от соответствующей координаты.

4. Определить значения коэффициентов передачи объекта по каждой моде входного воздействия.

Краткая теория

Рассмотрим случай моделирования теплового процесса (объекта) явным методом сеток с использованием дифференциальных уравнений в частных производных.

Одномерный объект

Имеется объект, уравнение теплопроводности которого можно представить в виде:

, (7.1)

, ,

где a – заданный коэффициент, - шаг дискретизации по времени, - шаг дискретизации по координате x.

Граничные условия, при которых следует решать уравнение (7.1), запишем в виде:

, , , .

Решать данное уравнение будем методом конечных разностей, преобразуя, получим:

,

, (7.2)

.

Рис. 7.4. Упрощенная блок-схема решения уравнения (7.2).

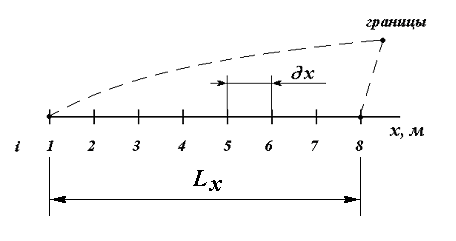
Для решения уравнения (4.2) необходимо знать граничные и начальные условия. Т.к. используется одна координата, границы расположены в ее крайних точках (см. рис. 4.3). В данном случае в точках 1 и 8.

С учетом рисунка в дискретной форме граничные условия можно записать в виде:

, , , (7.3)

где - управляющее воздействие. Функцией выхода будет .

При этом уравнение (4.2) можно решить численными методами согласно блок-схеме представленной на рис. 7.4.

Рис. 7.1. Дискретизация объекта.

Таблица. 7.1.

Исходные данные:

Lx	a
0.14	0.0001	0.02	100

Решая уравнение (7.2) с использованием данных табл. 7.1, при заданных граничных условиях получим:

Таблица. 7.2.

Рассчитанные значения температуры объекта

	Секции объекта
j
0	100	0	0	0	0	0	0	0
1	100	2.500	0	0	0	0	0	0
2	100	4.875	0.063	0	0	0	0	0
3	100	7.131	0.181	0.0015	0	0	0	0
4	100	9.275	0.350	0.0060	0	0	0	0
5	100	11.311	0.565	0.0144	0	0	0	0
6	100	13.245	0.819	0.0278	0.001	0	0	0
7	100	15.083	1.110	0.0469	0.001	0	0	0
8	100	16.829	1.431	0.0723	0.002	0	0	0
9	100	18.488	1.780	0.1045	0.004	0	0	0
10	100	20.063	2.153	0.1437	0.006	0	0	0
11	100	21.560	2.547	0.1904	0.010	0	0	0
12	100	22.982	2.959	0.2446	0.014	0.001	0	0
13	100	24.333	3.386	0.3063	0.019	0.001	0	0
14	100	25.616	3.825	0.3756	0.026	0.001	0	0
15	100	26.835	4.274	0.4525	0.034	0.002	0.001	0
16	100	27.994	4.731	0.5367	0.044	0.003	0.002	0
17	100	29.094	5.194	0.6281	0.055	0.004	0.002	0
18	100	30.139	5.662	0.7266	0.068	0.005	0.003	0
19	100	31.132	6.132	0.8318	0.083	0.006	0.004	0
20	100	32.076	6.604	0.9435	0.099	0.008	0.006	0
21	100	32.972	7.076	1.0614	0.118	0.010	0.008	0
22	100	33.823	7.546	1.1852	0.139	0.013	0.010	0
23	100	34.632	8.014	1.3146	0.161	0.015	0.011	0
24	100	35.401	8.480	1.4493	0.186	0.019	0.013	0
25	100	36.131	8.941	1.5888	0.213	0.022	0.015	0
26	100	36.824	9.397	1.7329	0.242	0.027	0.017	0
27	100	37.483	9.848	1.8811	0.273	0.031	0.019	0
…	100	…	…	…	…	…	…	0

С учетом полученных данных можно построить как график функции выхода (см. рис. 7.5), так и графики переходных процессов во всем объекте (см. рис. 7.6).

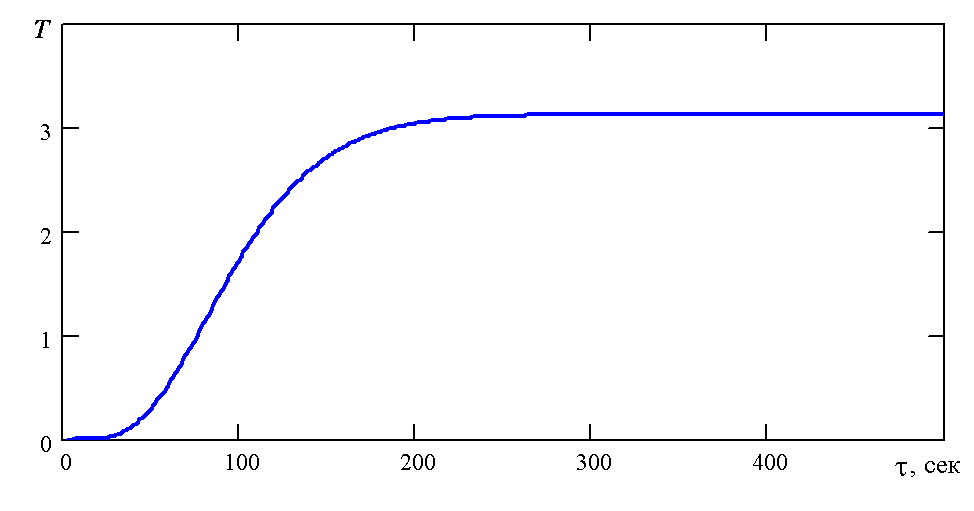
Рис. 7.5. График переходного процесса .

Рис. 7.6. Графики переходных процессов при .