
- •1Случайное событие. Частота события.
- •3. Необходимые сведения из комбинаторики. Их использование при решении задач теории вероятности
- •4.Теорема сложения вероятнорстей(для независимых и зависимых событий)
- •5.Независимые события. Теорема умножения вероятностей.
- •6.Формула полной вероятности
- •7.Повторные независимые испытания. Схема и формула Бернулли
- •8.Понятие случайной величины.Закон распределения случайной величины.
- •9.Математическое ожидание дискретной случайной величины. Его свойства. Дисперсия и среднеквадратичное отклонение дискретной случайной величины. Их свойства.
- •10.Непрерывная случайная величина Функция распределения случайной величины. Плотность распределения вероятностей. Их свойства.
- •15.Проверка статистических гипотез: критерий, уровень значимости.
- •3). Построение критерия проверки гипотезы.
- •15.Линейная регрессия.
- •1). Выборочная линейная среднеквадратическая регрессия.
9.Математическое ожидание дискретной случайной величины. Его свойства. Дисперсия и среднеквадратичное отклонение дискретной случайной величины. Их свойства.
. Математическим
ожиданием дискретной
случайной
величины
 называется сумма произведений всех
возможных значений
называется сумма произведений всех
возможных значений
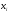 случайной величины на вероятности
случайной величины на вероятности
 этих значений:
этих значений:
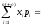
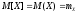 .
.
Свойства математического ожидания
Свойство
 .
Математическое
ожидание постоянной величины равно
этой постоянной
.
Математическое
ожидание постоянной величины равно
этой постоянной
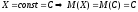 .
.
Доказательство.
Действительно,
пусть случайная величина
 равна
равна
 с вероятность
с вероятность
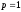 .
Тогда по определению математического
ожидания:
.
Тогда по определению математического
ожидания:
 .
.
Что и требовалось доказать.
Свойство
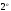 .
Постоянный
множитель можно вносить за знак
математического ожидания
.
Постоянный
множитель можно вносить за знак
математического ожидания
 ,
где
,
где
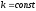 .
.
Доказательство.
Докажем для
случайной величины
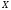 ,
которая принимает конечное число
,
которая принимает конечное число
 значений
значений
 .
По определению математического ожидания:
.
По определению математического ожидания:
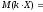
 .
.
Отсюда, вынося константу за знак суммы, получим:
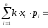
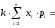
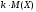 .
.
Что и требовалось доказать.
Свойство
 .
Математическое
ожидание суммы конечного числа случайных
величин равно сумме математических
ожиданий этих величин:
.
Математическое
ожидание суммы конечного числа случайных
величин равно сумме математических
ожиданий этих величин:
 .
.
Доказательство.
Докажем для
математического ожидания величины,
составленной из суммы двух случайных
величин
 и
и
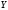 ,
причем случайная величина
,
причем случайная величина
 ,
принимает конечное число
,
принимает конечное число
 значений
значений
 ,
а случайная величина
,
а случайная величина
 ,
принимает конечное число
,
принимает конечное число
 значений
значений
 .
Тогда математическое ожидание суммы
двух величин
.
Тогда математическое ожидание суммы
двух величин
 и
и
 равно:
равно:


 .
.
Попробуем разобраться с первой двойной суммой
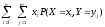 .
.
В
ней от значения
 не зависит внутренняя сумма, поэтому
вынесем
не зависит внутренняя сумма, поэтому
вынесем
 за знак этой суммы:
за знак этой суммы:
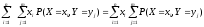 .
.
Событие,
состоящее в том, что
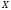 примет значение
примет значение
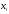 (вероятность этого события равна
(вероятность этого события равна
 ),
влечёт за собой событие, которое состоит
в том, что
),
влечёт за собой событие, которое состоит
в том, что
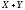 примет значения
примет значения
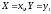 или
или
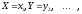 или
или
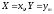 ,
,
а вероятности этих несовместных событий равны соответственно:
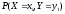 или
или
 или
или
 .
.
Тогда
вероятность
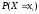 первоначального события
первоначального события
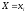 равна (по теореме о сложении вероятностей
несовместных событий):
равна (по теореме о сложении вероятностей
несовместных событий):
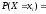
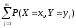 .
.
Поэтому первая двойная сумма равна:
 .
.
Последнее же равенство следует из определения математического ожидания.
Со второй двойной суммой поступим аналогично, но прежде заметим, что она не изменится, если поменять порядок суммирования:


(Это
известное свойство можно проверить,
расписав его для случаев
 или
или
 ).
А далее (вдоль по проторенной тропе):
).
А далее (вдоль по проторенной тропе):
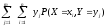

 .
.
Поэтому окончательно получаем:

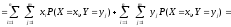
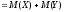 .
.
Что и требовалось доказать.
Свойство
 .
Математическое
ожидание произведения независимых
случайных величин равно произведению
их математических ожиданий:
.
Математическое
ожидание произведения независимых
случайных величин равно произведению
их математических ожиданий:
 .
.
. Дисперсией
случайной
величины
 называется величина:
называется величина:
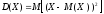 .
.
Дисперсия говорит о среднем квадрате отклонения от среднего.
Определение.
Средним квадратическим отклонением
случайной
величины
 называется величина:
называется величина:
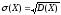 .
.
Среднее квадратическое отклонение говорит о среднем отклонении от среднего.
Для дискретной случайной величины дисперсия (естественно) имеет вид:
 .
.
Для
непрерывной случайной величины с
плотностью распределения вероятностей
 дисперсия
имеет вид:
дисперсия
имеет вид:
 .
.
Свойства дисперсии
Свойство
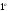 .
Дисперсия
постоянной величины равна нулю
.
Дисперсия
постоянной величины равна нулю
 .
.
Доказательство.
Действительно,
пусть случайная величина
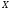 равна
равна
 с вероятность
с вероятность
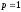 .
Поскольку тогда
.
Поскольку тогда
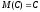 ,
то по определению дисперсии
,
то по определению дисперсии

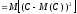
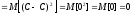 .
.
Что и требовалось доказать.
Свойство
 .
Постоянный
множитель можно вносить за знак
математического ожидания, но в
квадрате
.
Постоянный
множитель можно вносить за знак
математического ожидания, но в
квадрате
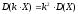 ,
где
,
где
 .
.
Доказательство.
Используя определение дисперсии и
свойство
 математического ожидания, получим:
математического ожидания, получим:


 .
.
Что и требовалось доказать.
Свойство
 .
Дисперсия
равна математическому ожиданию квадрата
минус квадрат математического ожидания
.
Дисперсия
равна математическому ожиданию квадрата
минус квадрат математического ожидания
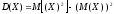
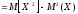 .
.
Доказательство.
Используя определение дисперсии и
свойство
 математического ожидания, получим:
математического ожидания, получим:
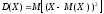

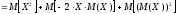 .
.
Поскольку
математическое ожидание – суть константа,
то по свойству
 ,
а затем по свойству
,
а затем по свойству
 математического ожидания, приходим к
следующему:
математического ожидания, приходим к
следующему:
 .
.
Теперь, приводя подобные, получаем:

Что и требовалось доказать.
Свойство
 .
Дисперсия
суммы двух независимых
случайных величин равна сумме дисперсий
этих величин:
.
Дисперсия
суммы двух независимых
случайных величин равна сумме дисперсий
этих величин:
 ,
если
,
если
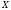 и
и
 - независимы.
- независимы.
Без доказательства (для заинтересовавшихся студентов это доказательство – повод повысить итоговую оценку).
Свойство
 .
Дисперсия
случайной величины ограничивает
вероятность ее отклонение от своего
математического ожидания (неравенство
Чебышева П.Л.:.
.
Дисперсия
случайной величины ограничивает
вероятность ее отклонение от своего
математического ожидания (неравенство
Чебышева П.Л.:.

