1.3. Основные свойства движения гироскопа

Рассмотрим сначала случай, когда на гироскоп не действуют никакие моменты, т.е. в (3) ^{M 0} (случай Эйлера-Пуансо). Такой гироскоп называют свободным. Чтобы ги- роскоп был свободным, в частности, должно выполняться условие совпадения его центра масс с центром О вращения, т.е. гироскоп должен быть астатическим. Для свободного

гироскопа согласно (3)

_G^& _0,

т.е G сохраняет свою величину и направление в инерциальном пространстве. Но посколь-

ку, согласно предыдущему п.1.2, с достаточно высокой точностью

^{G H ,} где ^{H Hz o,}

то отсюда вытекает первое основное свойство гироскопа: ось свободного гироскопа со-

храняет свою ориентацию в инерциальном пространстве.

Строго говоря, это свойство реализуется в некотором приближении, но тем точнее,

чем больше кинетический момент гироскопа.

Для практики важен ответ на вопрос: как изменится ориентация свободного гироско- па, если на него подействует какое-то кратковременное возмущение? Иными словами, ус- тойчиво ли свободный гироскоп сохраняет свою ориентацию? Для ответа на этот вопрос обратимся к уравнениям (8), полагая, что ориентация инерциальной и резалевой систем координат выбрана так, что положению гироскопа до воздействия на него возмущения соответствовали углы (t)= 0, (t) = 0. Запишем уравнения (8) в отклонениях от упо- мянутого невозмущенного движения в линейном приближении, сохранив, для упрощения записи, за отклонениями углов обозначения и :

^J _э^b&&

^J _э^a&&

H a^& 0,

H b^& 0.

(12)

_{Результатом кратковременного воздействия на гироскоп возмущения является появ-}

&

_{ление отклонений в углах a, b и в скоростях a}^&_{, b}^&

^{- обозначим их a}_о^{, b}_о^{, a&}_o ^{, b&}

- кото-

o

рые можно рассматривать как начальные условия для возмущенного движения гироскопа.

Решение системы (12) может быть легко получено; при указанных выше начальных усло-

_{виях оно имеет вид:}

&

a a _o

n ¹b_o

n ¹a^&_o sin nt

n ¹b_o cos nt,

₍₁₃₎

^{b b}_o

^{n 1a&}_o

^{n 1a&}_o ^{cos n}

^1b_o ^{sin nt,}

где

^{n J} _э ^1Н

&

. (14)

Нетрудно видеть, что соотношениям (13) соответствует такое движение гироскопа,

_{при котором его ось описывает конус, направление оси которого задается углами}

_{а полураствор равен}

&

a a_o

n ¹b_o, b b_o

^{n 1a&}_o ,

_{n 1 a& 2}

_{b&2 1/2}

o o ^.

Приведенные выкладки свидетельствуют о том, что в результате воздействия на гиро-

скоп кратковременного возмущения он изменит свою ориентацию, но величина этого из-

менения ограничена и тем меньше, чем меньше возмущение и больше Н. Иными словами, свободный гироскоп сохраняет свою ориентацию устойчиво, хотя и не асимптотически (т.е. его отклонения, вызванные воздействием возмущения, со временем не увеличивают- ся, но и не исчезают).

Пусть теперь гироскоп не является свободным и на него действует момент M . Тогда согласно (3)

_G^& _{M .}

_&

Поскольку _G

есть скорость конца вектора кинетического момента, то равенство (3)

применительно к гироскопу можно трактовать следующим образом: скорость конца век- тора кинетического момента гироскопа равна моменту, приложенному к гироскопу (теорема Резаля).

Итак, приложение к гироскопу момента вызывает изменение его ориентации, т.е. к

_{вращению оси гироскопа. Это вращение под действием момента называют прецессией}

гироскопа. Найдем скорость прецессии, обозначив ее

^w _п . Очевидно, что вектор ^w _п

ор-

тогонален оси гироскопа (поскольку угловая скорость, имеющая направление оси, к изме-

_{нению ориентации этой оси не приводит).}

Далее, ^w _п

ортогонален

^z&o, а модули этих двух векторов равны (это следует из само-

го определения понятия угловой скорости). Из сказанного вытекает следующее выраже-

ние для ^w _п

п

w z ^o z^&o

. (15)

Далее, поскольку с достаточной точностью

^{G Hz o} , (16)

_{то из (3) с учетом постоянства H получаем}

z^&o H ¹M

_{и после подстановки в (15)}

^w_п ^H

1 _z o

^M . (17)

Из изложенного вытекает второе основное свойство гироскопа: при действии на ги-

роскоп момента он прецессирует с угловой скоростью, определяемой равенством (17).

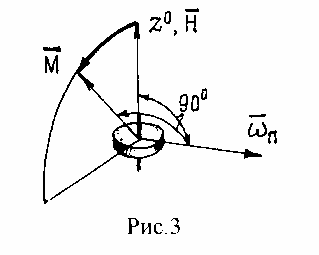
Нетрудно видеть, что прецессия происходит в плоскости, параллельной вектору мо- мента и оси гироскопа, при этом гироскоп стремится совместить свою ось с направлением момента по кратчайшему пути ,как показано на рис.3.Изложенное еще раз поясняет отме- ченную в п.1.2 особенность поведения гироскопа. Следует отметить, как и ранее, что опи- санное свойство реализуется с тем большей точностью, чем больше Н. Строго же оно не реализуется по той причине, что использованное при его выводе равенство (16) - приближенное, хотя и достаточно точное, - в нем не учтены инерционные члены, содер- жащие J_э. Но при тех же условиях получены и уравнения (10), (11), которые, следователь- но, отражают прецессионное движение, почему и называются прецессионными. Как уже отмечалось, при решении большинства прикладных задач оказывается вполне допусти- мым ограничиться рамками прецессионной теории.

Заметим, что в рамках этой теории гироскоп является безынерционным прибором: его пре- цессия возникает и исчезает одновременно с приложением и прекращением действия момен- та. При этом последний не совершает никакой работы, поскольку вызываемая им прецессия ги- роскопа происходит со скоростью, перпендику- лярной этому моменту.

Возникает естественный вопрос: как изме- нятся сформулированные выше утверждения, если не пренебрегать инерционными членами? Иными словами, насколько корректно ограничи- ваться рамками прецессионной теории? Для от-

вета на этот вопрос рассмотрим представляющий самостоятельный интерес случай дви- жения гироскопа, проанализированный Лагранжем и Пуассоном. Выводы, которые бу- дут сделаны по результатам этого рассмотрения, распространимы и на общий случай. В случае Лагранжа-Пуассона момент, прикладываемый к гироскопу, создается силой тяже-

сти P , т.к. полагается, что центр масс гироскопа смещен относительно центра вращения в направлении оси гироскопа на величину ^l (рис.4). Для упрощения рассмотрения будем полагать, что углы и малы, и в этом предположении запишем уравнения движения гироскопа (8), удерживая только члены первого порядка малости:

^J _э ^b&&

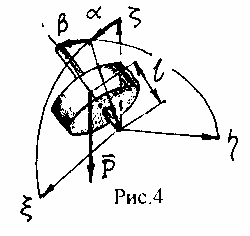
^J _э^a&&

Ha^&

Hb^&

Plb ,

Pla .

Решение этой линейной системы уравнений может быть получено достаточно просто и представимо в виде

_где

a a_п

b b_п

a_н ,

b _н ,

(18)

&

^a_п ^a_o

^{n 1b}_o

^cosw_п^t

^b_o ⁿ

^1a&_o ^{sin w}_п^t,

b_п b_o

n ¹a^&_o cosw_пt

&

a _o n

¹b_o sin w_пt,

₍₁₉₎

&

^a _н ^{n 1}

^b_o ^cosnt

^w_п ^b_o

^a&_o

sinnt ,

b _н n

_&

¹ a^&_o cosnt

w_пa_o b^&_o

sinnt .

^{Здесь a}_o^{, b}_o^,a&_o^{, b}_o ^{- начальные условия,}

_{=H/Jэ, п = Р} ^l _/H.

Из (18) и (19) следует, что движение гироскопа представляет собой сумму двух гармо- нических движений, одно из которых совершается с малой круговой частотой _п (ее ве- личина обратно пропорциональна большой величине Н), а другое - с высокой частотой n (величина которой прямо пропорциональна Н). Результирующее движение иллюстриру- ется рис.5.

^{Если пренебречь инерционными членами, устремив J}_э ^{к нулю, то при этом исчезнут}

_н и _н и останутся составляющие _п и _п. Следовательно, _п и _п описывают прецесси-

онное движение гироскопа.

Амплитуда этого движения определяется, как видно из (19), начальными условиями. Если теперь положить ^l =0, что эквивалентно исключению внешнего момента, низко- частотное прецессионное движение ис-

чезнет, но останется высокочастотное

движение.

Таким образом, это движение являет- ся собственным движением гироскопа. Оно называется нутационным движени- ем (или просто нутацией). Амплитуда ну- тации, как видно из (19), весьма мала, т.к. она обратно пропорциональна Н.

Таким образом, в разобранном случае

движение гироскопа складывается из низ- кочастотного прецессионного (вынуж- денного) движения и высокочастотного движения. При этом пренебрежение

инерционными членами, т.е. рассмотрение движения гироскопа в рамках прецессионной теории, эквивалентно пренебрежению нутационным движением, что в большинстве слу- чаев вполне допустимо вследствие его малости.