Доказательство. Необходимо доказать, что выполняется равенство

Х=Х1+(1-)Х2, т.е.существуют ли точки Х1 и Х2 , которые удовлетворяют системе ограничений (2). Докажем выполнение неравенств (2). Запишем точку Х в координатной форме:

(1) (1)

Х1 +(1- )Х1 Возьмём i -тое неравенство и

(1) (1) подставим в него Х

Х= Х2 +(1- )Х2

(1) (1)

Хn +(1- )Хn

Получим:

(1) (2)

i1 ( Х1 +(1- )Х1) + ………………………….+

(1) (2)

+………+ in ( Х1 +(1- )Хn) . Откуда

(1) (1) (2) (2)

( i1 Х1 + ….+ inХn + (1- ) ( i1 Х1 + ….+ inХn )).

Х1 и Х2 удовлетворяют системе ограничений, значит в сумме всё будет меньше bi, где можно взять любое i  [1,m]. Теорема доказана.

2. Максимум функции достигается в крайней точке ОДР.

Теорема. Целевая функция F задачи линейного программирования достигает своего максимального значения в угловой точке ОДР.

Если целевая функция принимает максимальное значение более, чем в одной крайней точке, то она достигает того же значения в каждой точке, являющейся выпуклой линейной комбинацией этих точек.

Доказательство.

Пусть ОДР ограничена и имеет конечное число крайних и угловых точек Х1, Х2, …, Хn.

Пусть Х0-оптимальное решение задачи (1)-(3). Если Х0- крайняя точка, то теорема доказана .

Пусть Х0-точка, являющаяся крайней точкой, но как любая допустимая точка она может быть представлена в виде выпуклой линейной комбинации крайних точек (см. теорему б/д).

ХO= 11 +22 +…+рр, где р

• i =1 и i 0.

i =1.

Запишем функцию F( ХO) = F(11 +22 +…+рр) = 1 F( Х1) + + 2 F( Х2) + …+ р F( Хр). Пусть максимум F( Хi)= F( Хk)=M ,

где 1 i  p.

F( ХO)  1М + 2 М +…+ рМ = (1 +2 +…+р) М = М.

ХO –оптимальная точка. F( ХO)  М

F( Х0)=M , F( Хk)=M.

F( ХO)  М

Хk-угловая точка. Т.О. максимум достигается в Хk.

Предположим, что максимум достигается в нескольких точках:

Х1, Х2,… , Хq, где qp.

Пусть Х является выпуклой линейной комбинацией этих точек:

Х= 11 +22 +…+qq, где q

• i =1 и i 0.

i =1.

Тогда значение функции в точках:

F( Х) = F(11 +22 +…+qq) = 1 F( Х1) + + 2 F( Х2) + …+

+q F( Хq) = (1 +2 +…+q) М = М.

Пусть область не ограничена. Введём дополнительное ограничение:

1 +2 +…+пS , где S-достаточно большое число.

Пусть теперь S1,S2,…,Sk –какие-то новые крайние точки, и пусть функция F достигает максимума в одной из них. Тогда максимальное значение зависит от S, поэтому S можно изменять, тем самым увеличивая максимум и делая функцию неограниченной.

Вывод. 1.ОДР-выпуклый многогранник .

2. Максимум достигается либо в одной крайней точке , либо в линейной комбинации.

Геометрическая интерпретация задачи.

Определение. Градиентом функции f (Х1, Х2, …, Хn.) в точке

0 0 0

Х0= (Х1, Х2,…,Хn ) называют вектор

 f (Х0) =  f(Х0)  f(Х0)  f(Х0)

 f(Х1) ,  f(Х2) ,  f(Хп)

Градиент всегда перпендикулярен касательной к функции и направлен в сторону возрастания функции.

Рассмотрим функцию L:  L=( C1, C2, …, Cn).

L (Х1,Х 2) = C1 Х1+ C2Х 2 max, C1, C2  0.

11Х1+12Х2  b1;

21Х1+22Х2  b2;

……………………

m1Х1+m2Х2  bm;

Х1,Х2  0 ;

max Происходит перемещение

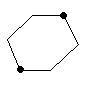
опорная

прямая рисунок 1.

Происходит перемещение опорной прямой к максимуму функции.

Геометрическая интерпретация доказанных свойств.