[Править] Решение уравнения Пуассона на поверхности полупроводника [править] Основные допущения теории поверхности

При теоретическом исследовании хода потенциала и распределения зарядов в полупроводнике вводятся следующие предположения:

1. . Полупроводник легированный однородно и имеет бесконечную толщину. Вторая часть этого предположения выполняется для кристаллов, толщина которых превышает несколько десятых миллиметра. Условие однородного легирования не всегда выполняется на практике вследствие перераспределения примесей при окислении поверхности. Это необходимо учитывать при исследовании режима плоских зон. В режимах аккумуляции и инверсии этим эффектом можно пренебречь.

2. . Полупроводник является невырожденным. В этом случае можно использовать статистику Максвелла-Больцмана. На практике в режимах аккумуляции и инверсии уровень Ферми может подходить близко к краям зон, что приводит к необходимости использования статистики Ферми-Дирака, что существенно затрудняет вычисления. Для упрощения рассматривают случай, когда уровень Ферми находится на несколько kT ниже/выше края соответствующих зоны.

3. . Ток через окисел, находящегося на поверхности полупроводника, отсутствует. Это предположение означает, что система является равновесная и поэтому можно пользоваться понятие уровня Ферми. Позднее при рассмотрении будет введен квазиривень Ферми, что позволит учесть неравновесные процессы и использовать полученные результаты при моделировании МДП-транзисторов.

4. . Плотность зарядов, локализованных на поверхности полупроводника и в объеме диэлектрика, не зависит от приложенного напряжения (электрического поля). На поверхности кремния, для которого приняты предосторожности по уменьшению и стабилизации поверхностных эффектов, эти условия выполняются.

5. . Эффекты, обусловленные наличием сильного электрического поля в полупроводнике, не учитываются. В общем случае изменение потенциала с расстоянием от поверхности может быть очень быстрой (при сильной инверсии), поэтому использование обычных полуклассических методов решения (например, использование уравнения Пуассона) требуют обоснования.

[Править] Заряды и потенциалы на поверхности полупроводника

Рассмотрим полупроводник p — типа. Плотность зарядов в полупроводнике ρ(x) определяется суммой зарядов электронов n, дырок p и примесей N:

. (1)

В случае невырожденного полупроводника

(2a)

, (2b)

где β=q/kT — обратный температурный потенциал, n_i — концентрация носителей в собственном полупроводнике. Поскольку при и , а поэтому из (1) и (2) следует, что

. (3)

Подстановка (2) и (3) в (1) дает:

(4)

а одномерное уравнение Пуассона запишется в виде:

где ε_s — диэлектрическая проницаемость полупроводника. В более компактной форме это уравнение будет:

(5)

где 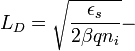дебаевской длина экранирования в собственном полупроводнике , u_F = βϕ_F,u = βϕ −  — безразмерные потенциалы. Интегрируя (5) от x до и учитывая, , u = 0 и , находим:

(6)

где знак «+» берется при u < 0. Таким образом, величина электрического поля на поверхности полупроводника будет:

(7)

Полный заряд на единицу поверхности полупроводника может быть найден из последнего уравнения путем использования теоремы Гаусса :

(8)

Для нахождения зависимости ρ(x) необходимо проинтегрировать (6) от x = 0 до x:

(9)

что в общем случае можно сделать численными методами. Подстановка (9) в (4) дает возможность определения зависимости ρ(x) для заданных значений ϕ_s и ϕ_F. В случае собственного полупроводника (u_F = 0) решение (9) находится в аналитическом виде. Уравнение (9) при этом переходит в

откуда находим:

(10)

а из (4) и (8) находим:

(11)

(12)

Интегрируя (11) и используя (5), можно найти выражение для полного заряда на единицу поверхности:

(13)

Разделив (13) на (12), находим:

Это соотношение определяет относительную величину заряда, который сосредоточен в слое от x = 0 до x, где потенциал равен u. С помощью (10) величина Q / Q_s выражается в явном виде через отношение x / L_D. Другой случай, допускающий аналитическое решение уравнения (9) — случай сильной инверсии на поверхности полупроводника:

(14)

Здесь в подкоренное выражение уравнения (9) учитывается только средний член, так что интегрирование дает:

(15)

Аналогичным образом из (4) находим:

или исключая u с помощью (15),

(16)

Необходимо отметить, что область использования (16) достаточно узкая, поскольку величина u не должна быть слишком большой, чтобы выполнялось предположение об отсутствии вырождения, и в то же время она не должна быть малой для выполнения условия (14).