4.8. Графический метод решения игр порядка и

Рассмотрим метод на примерах.

Пример 2.5. Пусть дана платежная матрица порядка :

Стратегии	Стратегии
	2	3	11
	7	5	2

Требуется найти решение игры.

Оптимальной является такая стратегия игрока , для которой функция

максимальна. Полагая последовательно , и , получим следующую задачу максимизации:

.

Так как , то эту задачу можно записать в виде:

(2.10)

при условии .

Задачу нелинейной оптимизации (2.10) нетрудно решить графически, как показано на рис. 2.1. Для этого на отрезке изобразим три прямые линии с уравнениями

(1): ,

(2): ,

(3): .

Тогда график функции представляет собой выделенную на рис. 2.1 ломаную линию. Максимальное значение этой функции можно найти, решив систему уравнений, составленную из (2)-го и (3)-го уравнений. Тогда . Отсюда находим

, , .

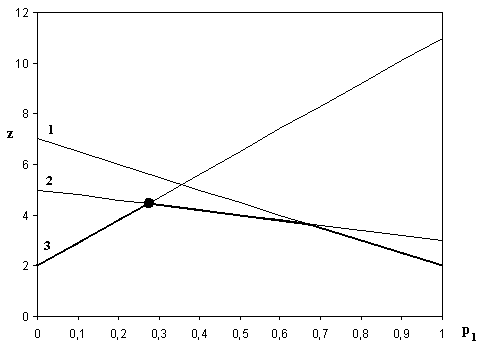
Рис. 2.1. Графическое решение задачи (2.10)

Так как точка максимума лежит на пересечении 2-й и 3-й прямых, то стратегия не входит в оптимальную стратегию игрока . Таким образом, , и мы можем найти его оптимальную стратегию при помощи матрицы

.

Для игры порядка получим , . Следовательно, .

Пример 2.6. Найти решение игры для платежной матрицы порядка :

Стратегии	Стратегии
	6	5
	4	6
	2	7
	1	8

Проведем сначала рассуждения с позиций игрока . Его оптимальной стратегией является такая стратегия , для которой функция

минимальна. Выбирая в качестве вектора: , , и , получим следующую задачу на минимум:

.

Поскольку , то имеем задачу:

(2.11)

при условии .

Задача (2.11) решается графически, как показано на рис. 2.2. Для этого на отрезке изобразим прямые линии с уравнениями

(1): ,

(2): ,

(3): ,

(4): .

Тогда график функции представляет собой выделенную на рис. 2.2 ломаную линию. Минимальное значение этой функции находится на пересечении 1-й и 4-й линий, следовательно, есть корень уравнения . Отсюда получим

, , .

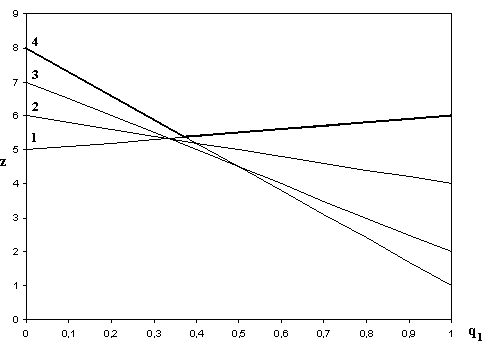
Рис. 2.2. Графическое решение задачи (2.11)

Чистые стратегии и не входят в оптимальную стратегию игрока , т.е. . Вероятности применения игроком стратегий и определяются из решения матричной игры порядка : . Эти вероятности равны , . В результате получим оптимальную стратегию игрока : .

4.9. Доминирование чистых стратегий

Исследование игры обычно начинается с упрощения платежной матрицы. Если в платежной матрице имеются заведомо невыгодные стратегии, то их можно исключить и тем самым уменьшить ее размерность. Рассмотрим, например, игру с матрицей

Стратегии игрока	Стратегии игрока
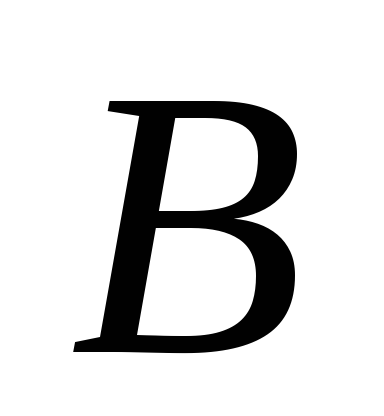
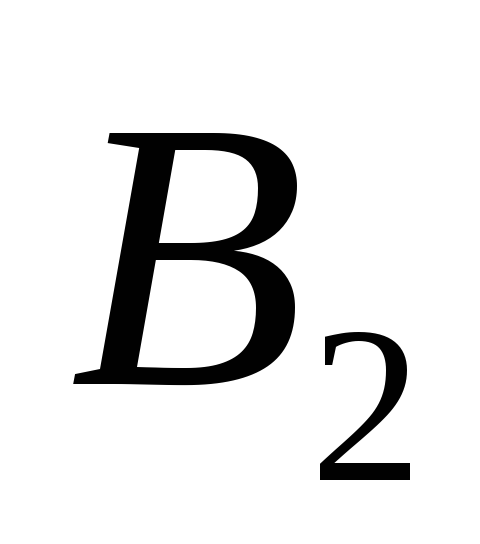
	3	0	4	-1
	5	2	6	1
	4	0	6	4

Сравнивая вторую строку матрицы с первой строкой, за­мечаем, что все элементы первой строки не превосходят соответствующих элементов второй строки. По этой причине говорят, что вторая строка доминирует над первой. Игрок , выбирая между стратегиями и , во всех случаях отдаст предпочтение стратегии ­, и, следовательно, вероятность выбора стратегии ­ в оптимальной стратегии первого игрока должна быть равна нулю: . Поэтому из матрицы можно удалить доминируемую первую строку и рассмотреть игру с новой матрицей:

Стратегии игрока	Стратегии игрока
	5	2	6	1

4

0

6

4

Строки новой матрицы несравнимы между собой, так как, например, 5>4, но 1<4. Сравнивая теперь столбцы матрицы, видим, что первый и третий столбец доминирует над вторым. Игрок , заинтересованный в меньшем проигрыше, предпочтет стратегию и, таким образом, в его оптимальной стратегии вероятности выбора стратегий и должны быть равны нулю: . Вычеркнув первый и третий столбцы, получим матрицу размерности :

Стратегии игрока	Стратегии игрока
	2	1
	0	4

Решив игру с этой матрицей, получим , , , , а также цену игры . Решением исходной игры будут, очевидно, стратегии , и цена игры .

Пример 2.7 (игра «в жулика»). Игрок располагает тремя картами: бубновым тузом, трефовым тузом, двойкой бубен; у игрока также три карты: бубновый туз, трефовый туз и двойка треф. В каждой партии игроки откладывают по одной своей карте и затем их сравнивают. Если обе карты окажутся одной масти, то игрок выигрывает количество очков, соответствующее отложенной им карте, при этом туз оценивается в одно очко, двойка – в два очка. Если карты разной масти, то игрок выигрывает количество очков, соответствующее его карте. Исключение составляет случай, когда обе карты окажутся двойками, тогда выигрыш принимается равным нулю. Найти оптимальные стратегии игроков и цену игры.

Составим платежную матрицу, исходя из условий игры

Стратегии игрока	Стратегии игрока
	(ТБ)	(ТТ)	(2Т)
(ТБ)	1	-1	-2
(ТТ)	-1	1	1
(2Б)	2	-1	0

Здесь ТБ означает туз бубен, ТТ – туз треф и т.д. На первый взгляд игра кажется ничейной, однако, ее решение приводит к другому заключению.

Сопоставляя строки платежной матрицы, видим, что первая строка доминируется третьей, и, значит, она может быть удалена. После этого можно удалить третий столбец, так как он доминирует над вторым. Новая матрица

Стратегии игрока	Стратегии игрока
	(ТБ)	(ТТ)
(ТТ)	-1	1
(2Б)	2	-1

имеет размерность . Решением игры с новой матрицей будут смешанные стратегии со следующими вероятностями чистых стратегий: , , , и цена игры . Исходная игра имеет оптимальные стратегии: , .

Как видим, игра «в жулика» оказалась выигрышной для игрока , поскольку цена игры – положительное число () и проигрышной для игрока .