Висновки

Під час виконання було розглянуто приклад реалізації …, в основі якої лежить алгоритм швидкого перетворення Фур’є за основою 4. Дана система обробляє вхідний сигнал, що є 32-розрядним і надходить з тактом, який дорівнює 20 нс. Вхідні дані оновлюються кожні 0.5 мс і представляються 256-ма вхідними відліками, що містять дійсну та уявну частину. .

В результаті набуто досвід у проектуванні обчислювальної системи, розглянуто основні компоненти, з яких вона складається, засвоєно алгоритми, на основі яких виконується обчислення.

Література

1. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов /Пер. с англ. А.Л.Зайцева, Э.Г.Назаренко, Н.Н.Тетекина; Под ред. Ю.Н.Александрова. - М.:Мир, 1978. - 848 с.

8. Цифровые фильтры и устройства обработи сигналов на интегральных микросхемах: Справочное пособие/Ф.Б.Высоцкий, В.И. Алексеев, В.П. Пачин и др.; Под ред. Б.Ф.Высоцкого.-М.: Радио и связь, 1984.-216с.

9. Куприянов М. С., Матюшкин Б. Д. Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. – Спб. : Политехника, 1998.

10. Марков С. Цифровые сигнальные процессоры. Книга 1, М.:фирма МИКРОАРТ, 1996-144 с.

11. Цифровой процессор обработки сигналов TMS32010 и его применение/Под ред. А.А.Ланнэ.-Л.:ВАС,1990.-296 с.

12. http://www.analog.com.

13. http://www.ti.com.

14. Бабак В.П., Хандецький А.І., Шрюфер Е. Обробка сигналів: підручник для вузів., К., Либідь, 1996.- 390с.

15. Мельник А.А. Проектирование поточного процессора БПФ на специализированных БИС.- Львов, 1990.- 43с.

16. Применение цифровой обработки сигналов/ Под ред. Э.Оппенгейма.- М. Мир, 1980.- 552с.

17. Сверхбольшие интегральные схемы и современная обработка сигналов: Пер. с англ.- М.: Радио и связь, 1989.- 472с.

18. Справочник по устройствам цифровой обработки информации/ Н.А.Виноградов, В.Н.Яковлев, В.В.Воскресенский и др.- К:Тэхника, 1988.- 455с.

19. Бондарев В.Н., Трестер Г., Чернега В.С. Цифровая обработка сигналов: методы и средства. Учебное пособие для вузов. 2-е изд. – Х.: Конус, 2001.- 398 с.

20. Гольденберг А. Ш., Матюшкин Б. Д., Поляк М. Н. Цифровая обработка сигналов. Справочник. –М.: Радио и связь, 1985-312с.

21. Цифровая обработка сигналов/ А.Б.Сергиенко – СПб.:Питер, 2002.-608с.

22. Шрюфер Е. Обробка сигналів. Цифрова обробка дискретизованих сигналів.- К.: Либідь, 1992.- 226с.

23. Яцимірський М. М. Швидкі алгоритми ортогональних тригонометричних перетворень. - Львів: Академічний Експрес, 1997. - 219 с.

Вступ

Алгоритм швидкого перетворення Фур'є – є оптимізованим за швидкодією способом обчислення дискретного перетворення Фур'є (ДПФ), що має складність O(Nlog₂N) на відміну від складності ДПФ порядку O(N²).

Розробка процесора ШПФ на ПЛІС забезпечує однокристальну реалізацію процесора з високою продуктивністю і можливістю реконфігурації структури.

Теоретичне підґрунтя

Основні визначення

Визначення 1. Дано кінцеву послідовність x₀, x₁, x₂,..., x_N-1 (у загальному випадку комплексних чисел). ДПФ полягає в пошуку послідовності X₀, X₁, X₂,..., X_N-1, елементи якої обчислюються за формулою:

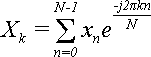(1)

Визначення 2. Зворотне ДПФ полягає в пошуку послідовності x₀, x₁, x₂,..., x_N-1, елементи якої обчислюються за формулою:

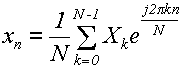(2)

Основною властивістю перетворень (1) і (2) є те, що з послідовності {x} отримується (при прямому перетворенні) послідовність {X}, а якщо застосувати до {X} зворотне перетворення, то знову отримується вихідна послідовність {x}.

Визначення 3. Величина

називається повертаючим множником.

Властивості повертаючих множників

При k = 1 

Пряме перетворення Фур'є можна виразити через повертаючі множники. Тоді формула (1) матиме вигляд:

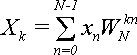(3)

Геометричне тлумачення повертаючих множників наведене на рис.1. Комплексне число (re^jφ) представлене у вигляді вектора, що виходить із початку координат (r - модуль числа, а φ – аргумент). Модуль відповідає довжині вектора, а аргумент - куту повороту. Модуль повертаючого множника . дорівнює одиниці, а фаза - 2π/N. Оскільки при множенні комплексних чисел, представлених у показниковій формі, їхні модулі перемножуються, а аргументи підсумовуються, множення вихідного числа на повертаючий множник не змінить довжину вектора, але змінить його кут. Тобто, відбудеться повертання вектора на кут 2π/N.

З формули (3) можна визначити геометричний зміст перетворення Фур'є таким чином: представити N комплексних чисел-векторів з набору {x}, кожне у вигляді суми векторів з набору {X}, повернених на кути, кратні 2π/N.

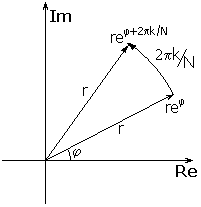
Рис.1.

Основні формули

Теореми, що пояснюють суть перетворення Фур’є (наведені без доведення).

Теорема 1. Якщо комплексне число представлене у вигляді e ^j2πN, де N - ціле, то e ^j2πN = 1.

Теорема 2. Величина періодична по k і по n з періодом N. Тобто, для будь-яких цілих l і m виконується рівність:

(4)

Теорема 3.

Для величини справедлива формула:

(5)

З наведених теорем визначається основна ідея алгоритму ШПФ:

1. Необхідно розділити суму (1) з N доданків на дві суми по N/2 доданків, і обчислити їх окремо. Для обчислення кожної з підсум, треба їх теж розділити на дві і т.д.

2. Необхідно повторно використовувати вже обчислені доданки.

При обчисленні алгоритму ШПФ застосовують або "проріджування за часом" (в першу суму попадають доданки з парними номерами, а в другу - з непарними), або "проріджування за частотою" (в першу суму попадають перші N/2 доданків, а в другу - інші). Обидва варіанти рівноцінні. В силу специфіки алгоритму доводиться застосовувати тільки N, що є ступенями 2. Розглянемо випадок проріджування за часом.

Теорема 4. Визначимо ще дві послідовності: {x_[even]} і {x_[odd]} через послідовність {x} таким чином:

x_[even]n = x_2n, x_[odd]n = x_2n+1, (6)

n = 0, 1,..., N/ 2-1

Нехай до цих послідовностей застосовані ДПФ і отримані результати у вигляді двох нових послідовностей {X_[even]} і {X_[odd]} по N/2 елементів у кожній.

Елементи послідовності {X} можна виразити через елементи послідовностей {X_[even]} і {X_[odd]} за формулою:

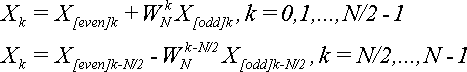(7).

Формула (7) дозволяє скоротити число множень удвічі (не враховуючи множень при обчисленні X_[even]k і X _[odd]k), якщо обчислювати X_k не послідовно від 0 до N - 1, а попарно: X₀ і X_N/2, X₁ і X_N/2+1,..., X_{N/ 2-1} і X_N. Пари утворяться за принципом: X_k і X_N/2+k.

Теорема 5. ДПФ можна обчислити і за формулою:

(8)

З теореми випливає, що можна не зберігати обчислені значення X_[even]k і X_[odd]k після обчислення чергової пари, і одне обчислення можна використовувати для обчислення двох елементів послідовності {X}.

На цьому кроці буде виконане N/2 множень комплексних чисел. Якщо застосувати подібні схеми для обчислення послідовностей {X_[even]} і {X_[odd]}, то кожна з них вимагатиме N/4 множень, разом ще N/2. Продовжуючи аналогічно далі log₂N разів, можна дійти до сум, що містять лише один доданок, так що загальна кількість множень рівна (N/2)log₂N.

Розглянемо ШПФ для різних N. Додамо ще один нижній індекс, який буде вказувати на загальну кількість елементів послідовності, до якої цей елемент належить. Тобто X_{R}k - це k-ий елемент послідовності {X_{R}} з R елементів. X_{R}[even]k - це k-ий елемент послідовності {X_{R}[even]} з R елементів, обчислений по парних елементах послідовності {X_{2R}}. X_{R}[odd]k - це k-ий елемент послідовності {X_{R}[odd]}, обчислений по непарних елементах послідовності {X_{2R}}.

У випадку, коли доданок лише один (N = 1) формула (1) спрощується до:

,

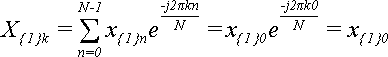Оскільки в цьому випадку k може бути рівне тільки 0, то X_{1}0 = x_{1}0, тобто, ДПФ над одним числом дає це ж саме число.

Для N = 2 за теоремою (5) отримаємо:

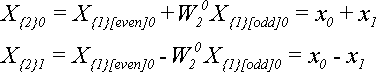
Для N = 4 за теоремою (5) отримаємо:

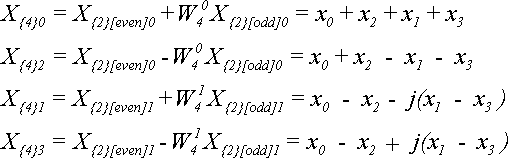
Звідси виходить, що якщо елементи вихідної послідовності були дійсними, то при збільшенні N елементи ДПФ стають комплексними.

Для N = 8 за теоремою (5) отримаємо:

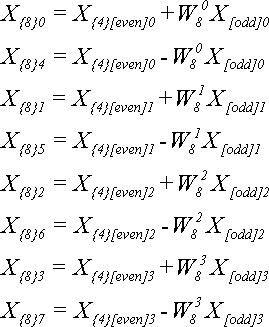
Необхідно звернути увагу, що на попередньому кроці використовувалися ступені W₄, а на цьому - ступені W₈. Зайвих обчислень можна уникнути, якщо врахувати, що

Тоді формули для N=4 будуть використовувати ті ж W-множники, що і формули для N=8:

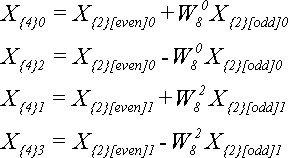
Висновок:

В основі алгоритму ШПФ лежать такі формули:

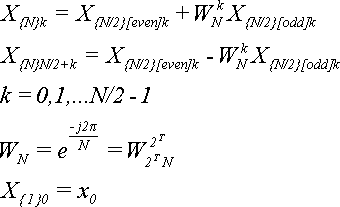(9)

Відомі два різновиди алгоритмів ШПФ - проріджування за часом (decimation in time - DIT) і проріджування по частоті (decimation in frequency - D1F), що мають однакову обчислювальну складність.

Алгоритм ШПФ із проріджуванням за часом

Нехай

Розділимо послідовність x(n) на парні (even) і непарні (odd) складові

Введемо підстановку n=2r для парних n і n=2k+1 для непарних n:

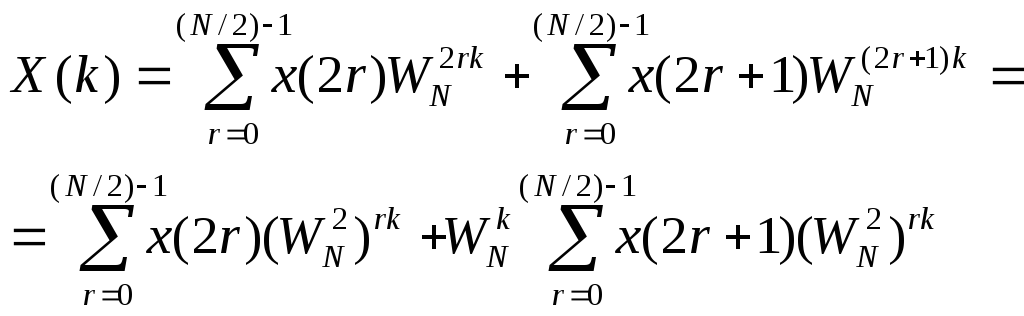
Тому, що

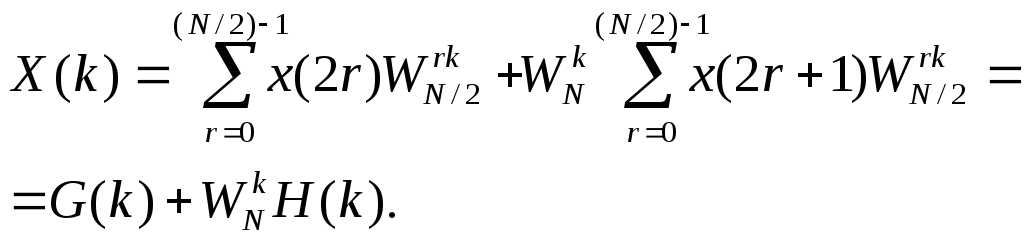
Необхідно зауважити, що і G(k), і H(k) в останній рівності можна трактувати як (N/2)-точкове ШПФ. Отже, N-точкове ШПФ можна обчислити за допомогою комбінування двох N/2-точкових ШПФ. Продовження рекурсії приводить до 2-точкових ШПФ. які виконуються без використання множень. На рис. 2 приведене 8-точкове ШПФ, побудоване за цією схемою. Причому, вхідна послідовність представлена в біт-інверсному виді.

З рис.2 видно, що обчислення ШПФ полягає в послідовному виконанні спеціальних операцій, названих "метеликом", що полягають у виконанні одного комплексного додавання, одного віднімання й одного множення. Віднімання виникає, оскільки

і

Створення VHDL-моделі пристрою

VHDL-код описує поведінку проектованої цифрової системи і є звичайним текстовим файлом. Виконання VHDL-опису проводиться за допомогою спеціальної програми - системи моделювання.

Система моделювання включає засоби, призначені для:

- організації проекту - визначення директорії проекту, розташування в ній необхідних файлів з вихідними VHDL-кодами, необхідними пакетами та бібліотеками VHDL-описів;

- компіляції - перетворення VHDL-кодів у внутрішнє представлення, яке і виконується (моделюється);

- збирання (лінкування);

- моделювання - виконання VHDL-кодів, представлених у внутрішній формі;

- візуалізації вихідних описів та результатів моделювання в різних формах - текстовій або графічній (часові діаграми).

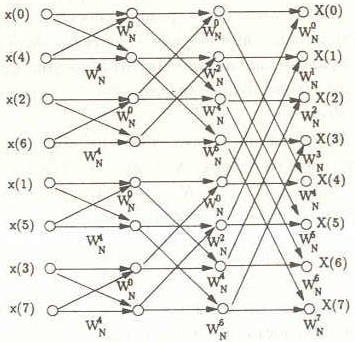
Рис.2.Алгоритм ШПФ з прорідженням за часом (N=8)