V. Комплексные числа

Системы действительных чисел недостаточно для решения квадратных уравнений. Простейшим из этих уравнений является уравнение x² + 1 = 0.

Определение. Полем комплексных чисел называется минимальное поле, содержащее в качестве подполя поле действительных чисел R и число i, с условием, что i² = -1.

Предположим, что поле, удовлетворяющее этому определению, существует, и исследуем, какими свойствами должно обладать это поле. Обозначим его C.

Поле C вместе с любыми действительными числами a, b и числом i должно содержать произведение bi и сумму a + bi.

Если a = c и b = d должно быть a + bi = c + di

Обратно, если a + bi = c + di, то a = c и b = d

Т.к. если , то (b - d)i = c – a , тогда i было бы действительным числом.

Следовательно a + bi = c + di  a = c и b = d (1)

В поле C должны выполняться законы коммутативности, ассоциативности и дистрибутивности.

(a + bi) + (c + di) = (a + c) + (b + d)i (2)

(a + bi)(c + di) = (ac - bd) + (ad + bc)i (3)

Если существует поле C, то оно должно содержать все числа вида a + bi, где a,b. Каждое число a + bi должно однозначно определяться парой (a,b) сложение и умножение должны производиться по правилам (2) и (3), т.е. если числа определяются парами действительных чисел (a,b) и (c,d), то сумма и произведение должны определяться соответственно парами:

(a + c,b + d) и (ac – bd,ad + bc)

Построим поле, являющиеся интерпретацией поля комплексных чисел, используя для этого пары действительных чисел.

Определение. Комплексным числом называется любая пара действительных чисел (a,b), поставленных в указанном порядке.

Определение. Два комплексных числа (a,b) и (c,d) называются равными тогда, и только тогда, когда a = c и b = d.

Следствие. Отношение равенства комплексных чисел обладает свойствами рефлексивности, симметричности и транзитивности.

Определение. Сложение комплексных чисел производится по правилу

(a,b) + (c,d) = (a + c,b + d)

Определение. Умножение комплексных чисел производится по правилу

(a,b) (c,d) = (ac – bd,ad + bc)

Следствие. Сложение и умножение комплексных чисел являются алгебраическими операциями, определенными в множестве всех комплексных чисел . Обе эти операции ассоциативны, коммутативны и связаны между собой законом дистрибутивности.

Из этого следует, что коммутативное кольцо.

1. Нулем кольца комплексных чисел будет число (0,0)

(a,b) + (0,0) = (a,b)

2. Числом, противоположным числу (a,b), будет число (-a,-b)

(a,b) + (-a,-b) = (0,0)

3. Единицей кольца будет число (1,0)

(a,b) (1,0) = (a,b)

Теорема. В множестве всех комплексных чисел каждое уравнение (a,b) (x,y) = (c,d) имеет единственное решение при (a,b) (0,0), т.е. при a² + b² 0

Доказательство.

Предположим, что уравнение имеет решение (x₁,y₁)

(a,b) (x₁,y₁) = (ax₁ – by₁,ay₁ + bx₁) = (c,d)

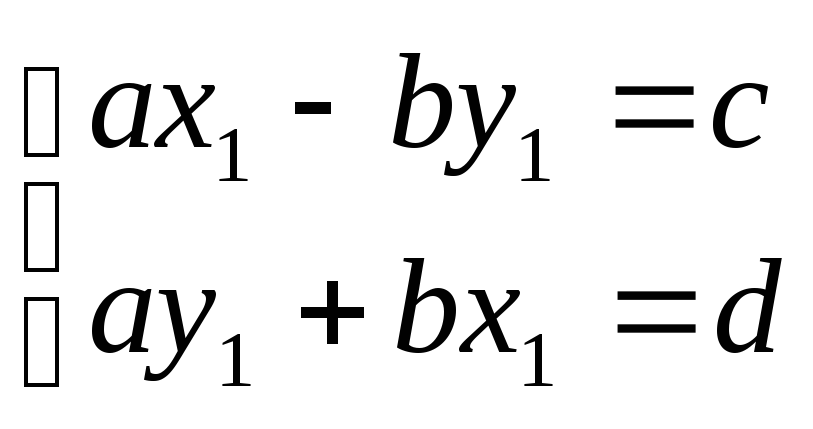
Таким образом, множество является полем.

Рассмотрим множество всех комплексных чисел вида (a,0), где a. Установим соответствие между множествами R и . (a,0) . Соответствие будет изоморфным, т.к. это соответствие взаимнооднозначное и из равенств

(a,0) + (b,0) = (c,0) и (a,0) (b,0) = (d,0)

всегда следуют верные равенства

a + b = c и ab = d.

Для построения поля C соответственные элементы при изоморфизме можно считать равными, т.е. (a,0) и a будем считать лишь различными формами записи одного и того же комплексного числа, а все остальные элементы (a,b) при b0 обоих полях и C одни и те же. Если для комплексного числа (0,1) ввести обозначение i, то

i² = (0,1) (0,1) = (-1,0) = -1 i – мнимая единица.

Из (b,0) = b и (0,1) = i => bi = (b,0) (0,1) = (0,b)

Комплексное число можно представить в виде записи:

(a,b) = (a,0) + (0,b) = a + bi

которая называется алгебраической формой записи комплексного числа.

Число a называется действительной частью, а число bi – мнимой частью комплексного числа.

Неотрицательное число называется модулем комплексного числа a + bi .

Числа z = a + bi и называются взаимно сопряженными.

Теорема. Множество M всех матриц вида , где a и b – любые действительные числа, изоморфно полю комплексных чисел C.

Доказательство.

a + bi

Это соответствие является взаимнооднозначным

(a + bi) + (c + di) = (a + c) + (b + d)i

+ = ;

(a + bi)(c + di) = (ac - bd) + (ad + bc)i

= .

Таким образом , причем M содержит поле изоморфное полю действительных чисел R.

состоит из матриц вида

Теорема. Поле комплексных чисел не может быть расположено.

Доказательство.

Во всяком расположенном поле квадрат любого отличного от нуля элемента больше нуля, но i0 и i² = -1 < 0, что и доказывает утверждение.