
- •В.Л. Шарстнёв компьютерные информационные технологии Курс лекций
- •1. Введение в курс “Компьютерные информационные технологии”
- •Тема 1.1. Основные понятия информационных технологий
- •Составляющие информационных технологий
- •Классификация информационных технологий.
- •Тема 1.2. Информационные ресурсы автоматизированных систем обработки экономической информации
- •Тема 1.3. Техническое обеспечение систем обработки экономической информации Классификация компьютеров
- •Периферийные устройства
- •Тема 1.4. Программное обеспечение обработки экономической информации Классификация компьютерных программ
- •Тема 1.5. Математическое обеспечение обработки экономической информации
- •Регрессионный и корреляционный анализ
- •Информационная поддержка процессов моделирования и управления
- •Тема 1.6. Технологии искусственного интеллекта
- •2. Сетевые информационные технологии
- •Тема 2.1. Компьютерные сети: основные понятия и принципы построения
- •Тема 2.2. Internet / Intranet – технологии
- •Обзор браузеров
- •Группы тегов нтмl
- •Назначение заголовка
- •Основные контейнеры заголовка
- •Теги тела документа
- •Теги управления разметкой
- •Теги управления отображением символов
- •Теги, управляющие формой отображения шрифта
- •Создание списков в html
- •Комментарии в языке html
- •Гипертекстовые ссылки
- •Использование графики в html
- •Активные изображения (map)
- •Средства описания таблиц в html
- •Задание формы в html
- •Тема 2.3. Специализированные компьютерные сети
- •Электронные деньги
- •Интернет-банкинг
- •Интернет-трейдинг
- •3. Корпоративные информационные технологии
- •Тема 3.1. Корпоративные информационные системы
- •Тема 3.2. Информационное обеспечение корпоративных информационных систем
- •4. Технологии обеспечения безопасности информационных систем
- •Тема 4.1. Информационная безопасность: основные понятия
- •Тема 4.2. Обеспечение безопасности информационных систем
- •5. Системы автоматизации в предметной области
- •Тема 5.1. Предметная область как объект автоматизации
- •Тема 5.2. Уровни автоматизации бизнес – процессов
- •6. Основы проектирования компьютерных информационных технологий
- •Тема 6.1. Реинжиниринг бизнес – процессов
- •Тема 6.2. Проектирование автоматизированных систем обработки информации
- •Шарстнёв Владимир Леонидович компьютерные информационные технологии
- •Редактор: н.С. Любочко
Регрессионный и корреляционный анализ
Регрессионный и корреляционный анализ позволяет установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких других величин X, и делать прогнозы значений Y. Параметр Y, значение которого нужно предсказывать, является зависимой переменной. Параметр X, значения которого нам известны заранее и который влияет на значения Y, называется независимой переменной. Например, X – величина затрат компании на рекламу своего товара, Y – объем продаж этого товара и т.д.
Корреляционная зависимость Y от X – это функциональная зависимость вида
![]() ,
,
где
![]() –
среднее арифметическое (условное
среднее)
всех возможных
значений параметра Y,
которые соответствуют значению
–
среднее арифметическое (условное
среднее)
всех возможных
значений параметра Y,
которые соответствуют значению
![]() .
Уравнение называется уравнением
регрессии Y
на X,
функция
.
Уравнение называется уравнением
регрессии Y
на X,
функция
![]() –
регрессией
Y
на X,
а ее график – линией
регрессии Y
на X.
–
регрессией
Y
на X,
а ее график – линией
регрессии Y
на X.
Основная задача регрессионного анализа – установление формы корреляционной связи, т.е. вида функции регрессии (линейная, квадратичная, показательная и т.д.).
Метод наименьших квадратов
Метод наименьших
квадратов
позволяет определить коэффициенты
уравнения регрессии таким образом,
чтобы точки, построенные по исходным
данным
![]() ,
лежали как можно ближе к точкам линии
регрессии. Формально это записывается
как минимизация суммы квадратов
отклонений (ошибок) функции регрессии
и исходных точек
,
лежали как можно ближе к точкам линии
регрессии. Формально это записывается
как минимизация суммы квадратов
отклонений (ошибок) функции регрессии
и исходных точек
![]() ,
,
где
![]() –
значение, вычисленное по уравнению
регрессии;
–
значение, вычисленное по уравнению
регрессии;
![]() –
отклонение
–
отклонение
![]() (ошибка, остаток); n –
количество пар исходных данных.
(ошибка, остаток); n –
количество пар исходных данных.
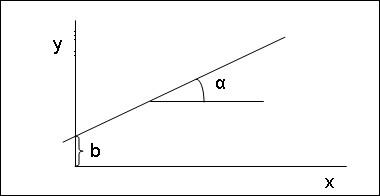
Простейший вариант модели - прямая линия на плоскости.
![]()
где
![]() b
- значение y при x=0;
a=tg(α)
- тангенс угла наклона прямой по отношению
к оси x.
b
- значение y при x=0;
a=tg(α)
- тангенс угла наклона прямой по отношению
к оси x.
![]()
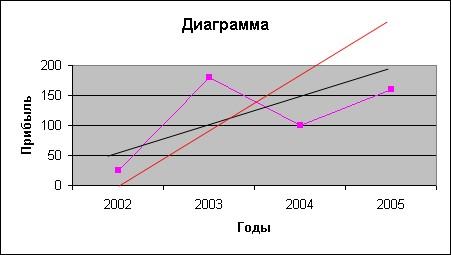
 Возможные
варианты модели
Возможные
варианты модели
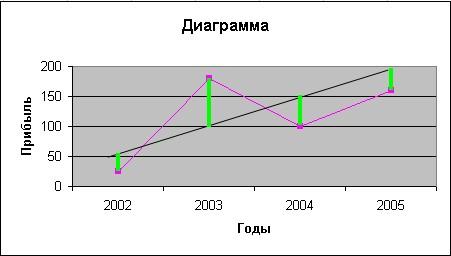
 Анализ
отклонений
Анализ
отклонений
 Первый
шаг
Первый
шаг
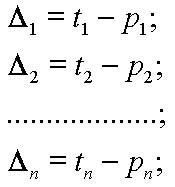 Второй
шаг
Второй
шаг
![]()
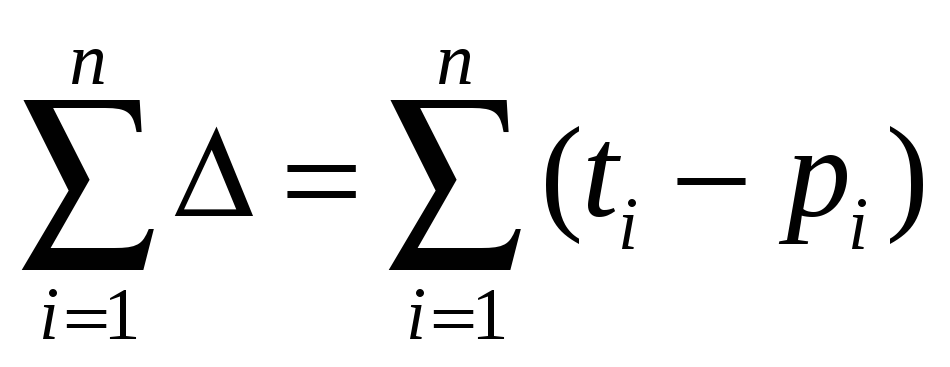 Третий
шаг
Третий
шаг
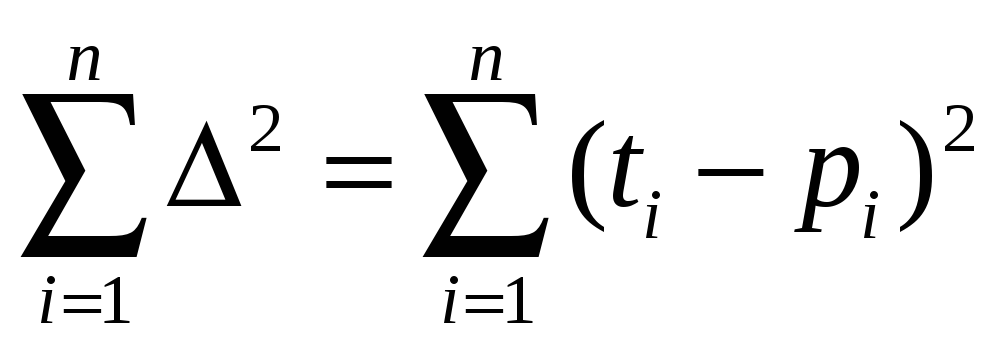 Четвертый
шаг
Четвертый
шаг
 Пятый
шаг
Пятый
шаг
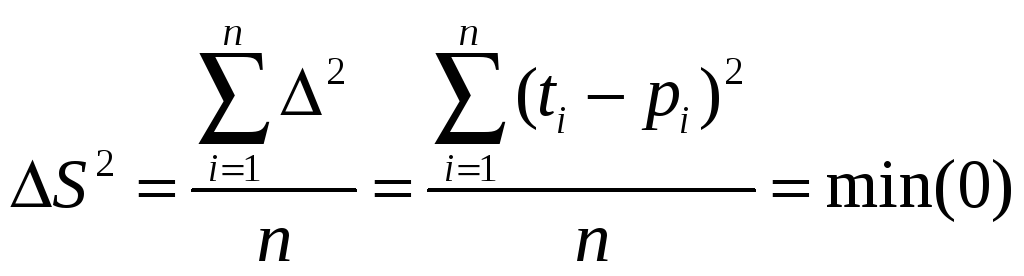
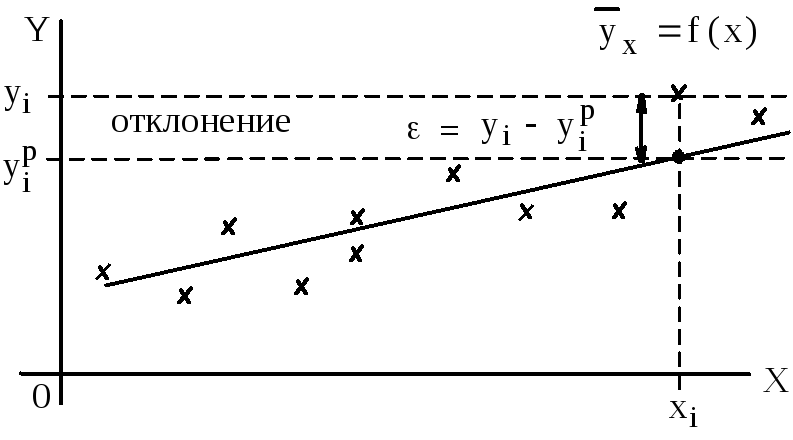
Понятие отклонения
![]() для случая линейной регрессии
для случая линейной регрессии
В регрессионном
анализе предполагается, что математическое
ожидание случайной величины
![]() равно нулю и ее дисперсия одинакова для
всех наблюдаемых значений Y.
Отсюда следует, что рассеяние данных
возле линии регрессии должно быть
одинаково при всех значениях параметра
X.
В случае, показанном на рисунке,
приведенном ниже, данные распределяются
вдоль линии регрессии неравномерно,
поэтому метод наименьших квадратов в
этом случае неприменим.
равно нулю и ее дисперсия одинакова для
всех наблюдаемых значений Y.
Отсюда следует, что рассеяние данных
возле линии регрессии должно быть
одинаково при всех значениях параметра
X.
В случае, показанном на рисунке,
приведенном ниже, данные распределяются
вдоль линии регрессии неравномерно,
поэтому метод наименьших квадратов в
этом случае неприменим.

Неравномерное распределение исходных точек вдоль линии регрессии
Основная задача корреляционного анализа
Основная задача
корреляционного анализа –
оценка
тесноты
(силы) корреляционной связи. Теснота
корреляционной зависимости Y
от X
оценивается по величине рассеяния
значений параметра Y
вокруг условного среднего
![]() .
Большое рассеяние говорит о слабой
зависимости Y
от X,
либо об ее отсутствии и, наоборот, малое
рассеяние указывает на наличие достаточно
сильной зависимости.
.
Большое рассеяние говорит о слабой
зависимости Y
от X,
либо об ее отсутствии и, наоборот, малое
рассеяние указывает на наличие достаточно
сильной зависимости.
Коэффициент
детерминации (по другому –
детерминированности)
![]() показывает, на сколько процентов (
показывает, на сколько процентов (![]() )
найденная функция регрессии описывает
связь между исходными значениями
параметров X
и Y
)
найденная функция регрессии описывает
связь между исходными значениями
параметров X
и Y
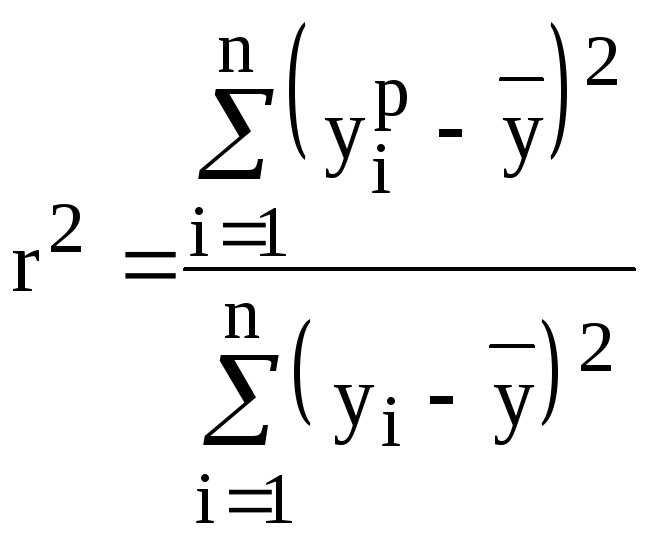 ,
,
где
![]() –
объясненная вариация;
–
объясненная вариация;
![]() –
общая вариация.
–
общая вариация.
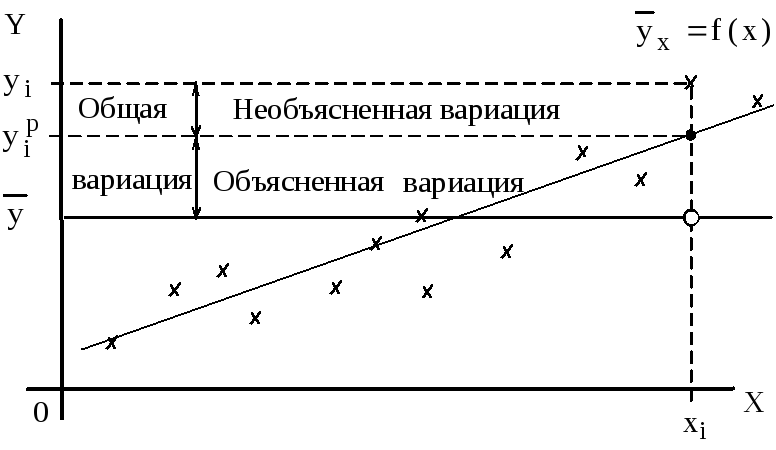
Графическая интерпретация коэффициента детерминации
для случая линейной регрессии
Соответственно,
величина
![]() показывает, сколько процентов вариации
параметра Y
обусловлены факторами, не включенными
в регрессионную модель. При высоком (
показывает, сколько процентов вариации
параметра Y
обусловлены факторами, не включенными
в регрессионную модель. При высоком (![]() )
значении коэффициента детерминации
можно делать прогноз
)
значении коэффициента детерминации
можно делать прогноз
![]() для конкретного значения
для конкретного значения
![]() .
.
Линейная регрессия
Коэффициенты
линейной
регрессии
![]() вычисляются по следующим формулам (все
суммы берутся по n
парам исходных данных)
вычисляются по следующим формулам (все
суммы берутся по n
парам исходных данных)
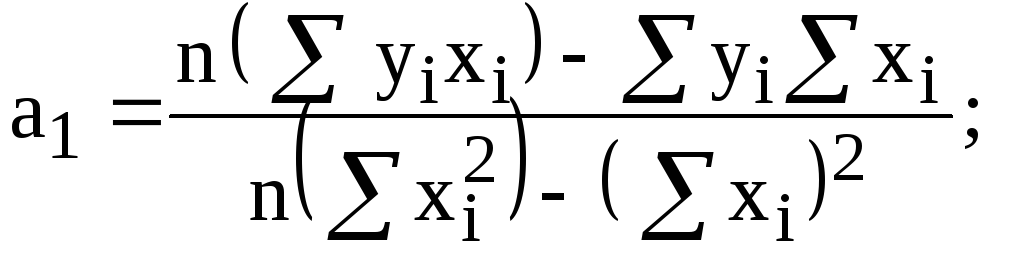
![]() .
.
Нелинейная регрессия
Рассмотрим наиболее простые случаи нелинейной регрессии: гиперболу, экспоненту и параболу. При нахождении коэффициентов гиперболы и экспоненты используют прием приведения нелинейной регрессионной зависимости к линейному виду. Это позволяет использовать для вычисления коэффициентов функций регрессии формулы линейной зависимости.
Гипербола
При нахождении
гиперболы
![]() вводят новую переменную
вводят новую переменную
![]() ,
тогда уравнение гиперболы принимает
линейный вид
,
тогда уравнение гиперболы принимает
линейный вид
![]() .
После этого используют формулы для
нахождений линейной функции, но вместо
значений
.
После этого используют формулы для
нахождений линейной функции, но вместо
значений
![]() используются значения
используются значения
![]()
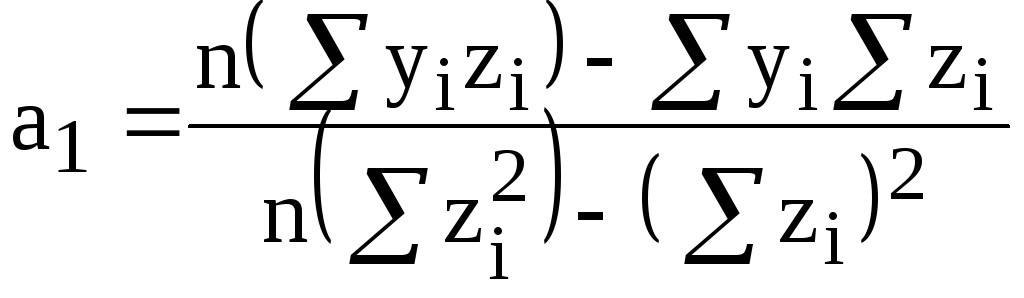 ;
;
![]() .
.
Экспонента
Для приведения к
линейному виду экспоненты
![]() проводят логарифмирование
проводят логарифмирование
![]() ;
;
![]() ;
;
![]() .
.
Введя переменные
![]() и
и
![]() ,
тогда
,
тогда
![]() ,
откуда следует, что можно применять
формулы линейной зависимости, в которых
вместо значений
,
откуда следует, что можно применять
формулы линейной зависимости, в которых
вместо значений
![]() надо использовать
надо использовать
![]()
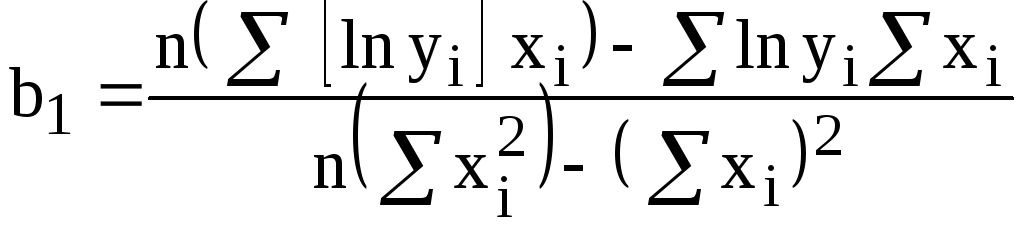 ;
;
![]() .
.
При этом получаем
численные значения коэффициентов
![]() и
и
![]() ,
от которых надо перейти к
,
от которых надо перейти к
![]() и
и
![]() ,
используемых в модели экспоненты. Исходя
из введенных обозначений и определения
логарифма, получаем
,
используемых в модели экспоненты. Исходя
из введенных обозначений и определения
логарифма, получаем
![]() ,
,
![]() .
.
Парабола
Для
нахождения
коэффициентов параболы
![]() необходимо решить линейную систему из
трех уравнений
необходимо решить линейную систему из
трех уравнений
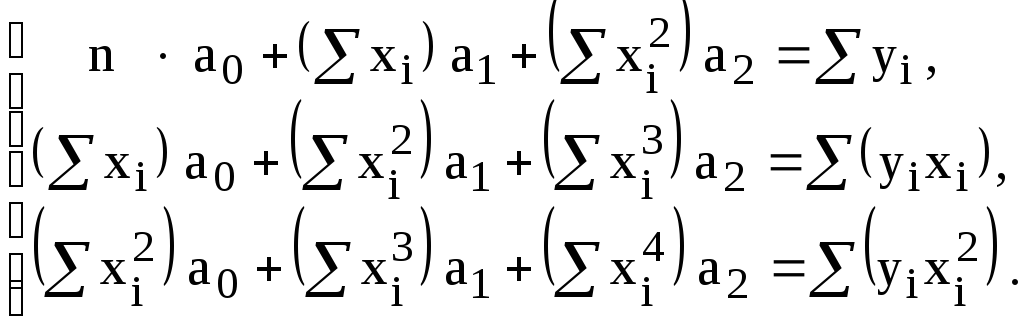
При вычислении
коэффициента детерминации экспоненты
все значения параметра Y
(исходные, регрессионные, среднее)
необходимо заменить на их логарифмы,
например,
![]() –
на
–
на
![]() и т.д.
и т.д.
