1.Наращение и дисконтирование потоков денежных сумм.

В реальной практике, как правило, приходится иметь дело не с единичными суммами, а с некоторыми потоками денежных сумм, которые предприятие реально и регулярно выплачивает либо получает. Денежный поток принято изображать на временной линии, как это показано на рисунке.

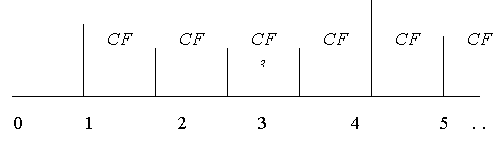
Элемент денежного потока принято обозначать CFk (от Cash Flow), где k - номер периода, в который рассматривается денежный поток. Настоящее значение денежного потока обозначено PV ( Present Value), а будущее значение - FV ( Future Value).

Наращение денежных потоков осуществляется с помощью многократного использования формулы (7):

,

или

    .                (20)

Пример. После внедрения мероприятия по снижению административных издержек предприятие планирует получить экономию $1,000 в год. Сэкономленные деньги предполагается размещать на депозитный счет (под 5 % годовых) с тем, чтобы через 5 лет накопленные деньги использовать дляинвестирования . Какая сумма окажется на банковском счету предприятия?

            Решим задачу с использованием временной линии.

            

           

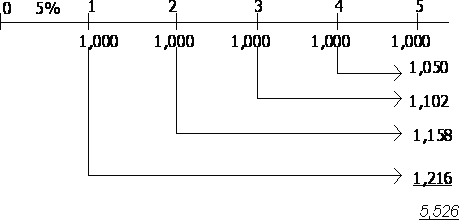
Таким образом, через 5 лет предприятие накопит $5,526, которые сможет инвестировать.

В данном случае денежный поток состоит из одинаковых денежных сумм ежегодно. Такой поток называется аннуитетом. Для вычисления будущего значения аннуитета используется формула

,                                                    (21)

которая следует из (20) при CFk = const.

            Расчет будущего значения аннуитета может производиться с помощью специальных финансовых таблиц. Фрагмент этих таблиц помещен в приложении  (таблица 3). В частности, с помощью таблицы 3 при r = 5% и n = 5 получаем множитель 5.526, который соответствует результату расчета примера.

            Для произвольного значения процентной ставки можно воспользоваться следующей конечной формулой для наращения аннуитета, которая легко получается путем использования суммирования убывающей геометрической прогрессии:

           .                                                          (211)

            Дисконтирование денежных потоков осуществляется путем многократного использования формулы (8), что в конечном итоге приводит к следующему выражению:

,

или

                                                 .     

Пример. Рассмотрим денежный поток с неодинаковыми элементами CF1=100, CF2=200, CF3=200, CF4=200, CF5=200, CF6=0, CF7=1,000, для которого необходимо определить современное значение (при показателе дисконта 6%). Решение проводим с помощью временной линии:

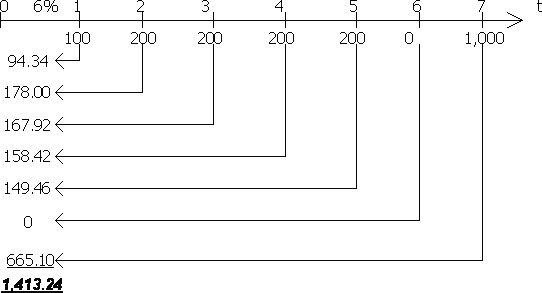
            Вычисление дисконтированных значений отдельных сумм  можно производить путем использования таблицы 2, помещенной в приложении.

            Дисконтирование аннуитета (CFj = const) осуществляется по формуле

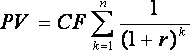                        .                                                       (23)

Для расчета настоящего (современного) значения аннуитета может быть использована таблица 4 приложения или следующее конечное соотношение:

                        .                                                                    (231)

Пример. Предприятие приобрело облигации муниципального займа , которые приносят ему доход $15,000, и хочет использовать эти деньги для развития собственного производства. Предприятие оценивает прибыльность инвестирования получаемых каждый год $15,000 в 12 %. Необходимо определить настоящее значение этого денежного потока.

            Решение проведем с помощью таблицы:

Год	Множитель дисконтированияпри 12%	Поток денег	Настоящее значение
1	0.893	$15,000	$13,395
2	0.797	$15,000	$11,955
3	0.712	$15,000	$10,680
4	0.636	$15,000	$9,540
5	0.567	$15,000	$8,505

По результатам расчетов мы видим, что:

• дисконтированное значение денежного потока существенно меньше арифметической суммы элементов денежного потока,

• чем дальше мы заходим во времени, тем меньше настоящее значение денег: $15,000 через год стоят сейчас $13,395; $15,000 через 5 лет стоят сейчас $8,505.

            Задача может быть решена также с помощью таблицы 4 приложения. При r = 12% и n = 5 по таблице находим множитель дисконтирования 3.605.

            Современное значение бесконечного (по времени) потока денежных средств определяется по формуле:

                                   ,                                                                  (24)

которая получается путем суммирования бесконечного ряда, определяемого формулой (23) при .

2.Наращение простых процентов

Основные термины — единичный промежуток начисления и ставка процента. Ставку процента обозначаем i. Фиксируем какую-нибудь сумму Р. При наращении простых процентов по ставке (каждая следующая сумма больше предыдущей на долю i от начальной суммы Р, т.е. на iP. К концу единичного промежутка начисления сумма Р возрастет на iPи станет Р1=Р+iP=Р(1+i), к концу 2-го промежутка начисления эта сумма возрастет еще на iPи станет Р2=Р1+iР=Р(1+i)+iР=P(i+2i) и т.д. К концу n-го промежутка начисления наращенная сумма станет Pn=P(1+ni). Таким образом, последовательность наращенных сумм P,Pi,...,Pn есть арифметическая прогрессия с начальным членом Р и разностью iP.

Пример 1.

Пусть Р=1000, i=10%, т.е. как доля i=0,1. Следовательно, наращенные по простым процентам суммы таковы:

1000, 1000+0,1*1000=1000+100=1100,

1100+100=1200, 1200+100=1300.

Пример 2.

Годовая ставка простых процентов равна 12,5%. Через сколько лет начальная сумма удвоится?

Решение: Надо решить неравенство: (1+0,125*n)≥ 2, т.е.0,125*n≥1. Получаем n≥1/0,125. Ответ: через 8 лет.

Формула наращения простых процентов Р=Р(1+ni), выведенная для целых положительных n, вполне может применяться и для нецелых t.

Сумма Р, наращенная по ставке i простых процентов, через tпромежутков начисления станет Рt=Р(1+ti).

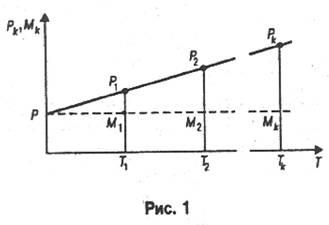
Разность наращенной суммы и начальной называется процентными деньгами. При наращении простых процентов процентные деньги растут в арифметической прогрессии. Графически это показано на рис. 1, где Р - начальная сумма, отрезки PkTk — наращенные суммы и отрезки PkMk — процентные деньги.

. Наращение сложных процентов

Наращивание сложных процентов по ставке i каждая следующая сумма возрастает на долю i от предыдущей. Таким образом, к концу единичного промежутка начисления сумма Р возрастет на долю i и станет P1=P+iP=P(1+i), к концу 2-го промежутка начисления эта сумма, возрастет еще на долю i от P1 и станетP2=P1+iP1=P(1+i)+iP(1+i)=P(1+i)2 и т.д. К концу n-го промежутка начисления наращенная сумма станет Pn=Р(1+i)n. Таким образом, последовательность наращенных сумм P, P1,…, Pn есть геометрическая прогрессия с начальным членом Pи знаменателем прогрессии (1+i).  Пусть P=1000, i=10%, т.е. доля i=0,1. Следовательно, наращенные по сложным процентам суммы таковы:  1000,1000+0,1* 1000=1000+100=1100, 1100+0,1*1100=1210, 1210+0,1*1210=1331,1  и т.д.  Пример 4.  Годовая ставка сложных процентов равна 8%. Через сколько лет начальная сумма удвоится?  Решение: Надо решить неравенство: (1+0,08)n≥2. Логарифмируем по основанию натуральных логарифмов и получаем n≥ln(2)/ln(1,08). Ответ: через 9 лет.  Из этого примера видно, что вычисления со сложными процентами более сложные, чем с простыми. Для занятий по финансовой математике  необходимо иметь хороший калькулятор (достаточно, чтобы можно было возводить любое положительное число в любую степень).  Формула наращения сложных процентов Pn=Р(1+i)n, выведенная для целых положительных п, может применяться и для нецелых t.  Сумма Р, наращенная по ставке i сложных процентов, через tпромежутков начисления станет Pt=Р(1+i)t.  Пример 5.  13 января в банк положили сумму 1000 до востребования под ставку 12% годовых сложных процентов. Какую сумму снимет вкладчик 1 сентября?  Решение: Воспользуемся формулой наращения сложных процентов Pt=Р(1+i)t. Но как вычислить t? Надо признать, что однозначного ответа в этой ситуации нет. Изберем самый простой вариант: будем считать, что в году 360 дней, в квартале — 90, в одном месяце — 30 и т.д. (учтем, что в году есть несколько праздничных дней и т.д.). Тогда t=(30*7+17)/360 и искомая сумма есть 1074.  При работе со сложными процентами иногда для приближенного оценивания полезно следующее правило.  Правило 72.  Если процентная ставка есть α, то удвоение капитала по такой ставке происходит примерно за 72 α лет.  Например, согласно этому правилу при ставке 8%, удвоение капитала происходит за 24 года.  Это правило применяется для небольших ставок