
- •Задачи для программирования по темам
- •Направление ″бизнес-информатика″, специальность ″математические методы в экономике″
- •1 . Обходы графа . Вычисление числа компонент связности графа.
- •2. Алгоритмы поиска путей в графе.
- •3. Алгоритмы нахождения минимального остова в графе
- •4. Хроматическое число графа. Алгоритм правильной раскраски вершин графа методом перебора с возвратами.
- •5. Транспортные сети. Теорема форда-фалкерсона о максимальном потоке в транспортной сети
- •6А. Варианты задач для групп по направлению ″бизнес-информатика″ тема ″транспортные сети″
- •6Б. Варианты задач для групп по специальности ″математические методы в экономике″
- •7.Задачи по теме ″рекурсивные функции″.
- •1. Доказать, что следующие функции примитивно рекурсивны:
- •8. Задачи по теме ″машины тьюринга″
- •2. (Гаврилов г. П., Сапоженко а.А. Задачник. С. 220-221, идея из № 1.2.) Построить машину в алфавите , , которая:
- •3. (Гаврилов г. П., Сапоженко а.А. Задачник. С. 221, № 1.3.) По заданной машине Тьюринга и начальной конфигурации найти заключительную конфигурацию:
- •4. (Лавров и.А., Максимова л.Л. С. 138, № 1.) Какую функцию вычисляет машина Тьюринга со следующей программой п:
- •5. (Лавров и.А., Максимова л.Л. С. 139, № 5.) Построить следующие машины Тьюринга в алфавите , , начальную конфигурацию в заключительную конфигурацию :
4. Хроматическое число графа. Алгоритм правильной раскраски вершин графа методом перебора с возвратами.
Определения и постановка задачи.
Даны
простой неориентированный граф
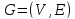 с множеством вершин
с множеством вершин
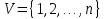 и множеством рёбер
и множеством рёбер
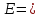
 (граф простой, значит. без петель и
кратных дуг).
(граф простой, значит. без петель и
кратных дуг).
Вершинная
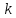 -раскраска
графа – это присвоение его вершинам
цветов из множества
-раскраска
графа – это присвоение его вершинам
цветов из множества
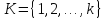 .
Раскраска называется правильной,
если никакие две смежные вершины не
получают одного цвета.
.
Раскраска называется правильной,
если никакие две смежные вершины не
получают одного цвета.
Хроматическим
числом
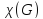 графа
графа
 называется минимальное число
называется минимальное число
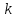 ,
при котором существует правильная
раскраска вершин графа в
,
при котором существует правильная
раскраска вершин графа в
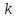 цветов.
цветов.
Очевидно,
что
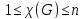 .
.
Задача:
вычислить
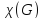 .
.
Функция
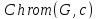 возвращает значение
возвращает значение
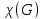 для графа
для графа
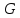 ,
заданного каким-либо образом (например,
матрицей или структурой смежностей).
Попутно вычисляется вектор
,
заданного каким-либо образом (например,
матрицей или структурой смежностей).
Попутно вычисляется вектор
 ,
где
,
где
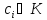 –
цвет, который получает
–
цвет, который получает
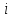 -ая
вершина. При вычислении
-ая
вершина. При вычислении
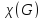 используется вспомогательная функция
используется вспомогательная функция
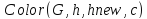 ,
возвращающая значение
,
возвращающая значение
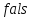 e
(ложь), если правильная
e
(ложь), если правильная
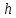 -раскраска
графа
-раскраска
графа
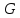 не существует, и возвращает значение
не существует, и возвращает значение
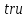 e,
если существует; в последнем случае
вычисляется значение
e,
если существует; в последнем случае
вычисляется значение
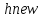 –
число использованных красок.
–
число использованных красок.
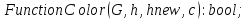
 если
раскраска существует, то можно считать,
что вершина 1 получила цвет 1
если
раскраска существует, то можно считать,
что вершина 1 получила цвет 1
for
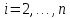 do
do
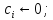 остальные
вершины пока цвета не имеют
остальные
вершины пока цвета не имеют
i← 2;
Далее
поиск правильной
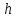 -раскраски
осуществляется методом перебора с
возвратами
-раскраски
осуществляется методом перебора с
возвратами
while
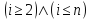 do
начинаем
раскраску со второй вершины
do
начинаем
раскраску со второй вершины
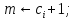
if
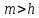 then {назад:
then {назад:
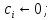
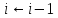 }
}
else
if
цвет
вершин, смежных с
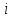 -ой
вершиной, отличен от
-ой
вершиной, отличен от
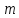
then
{вперед:
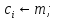
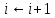 }
}
od; конец цикла while
if
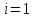 then
return (false)
then
return (false)
else
{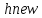 ←
число различных цветов в
←
число различных цветов в
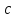 ;
return
(true)}.
;
return
(true)}.
Теперь вычисляем хроматическое число графа
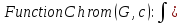 ;
;
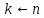 ;
;
for
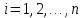 do
do
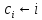 ;
;
while
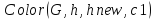 do
do
{ ;
; ;
;
 ←
←
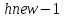 };
};
return
(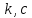 ).
).
5. Транспортные сети. Теорема форда-фалкерсона о максимальном потоке в транспортной сети
Определение.
Транспортная сеть
− это
связный ориентированный граф
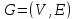 без петель, удовлетворяющий
следующим условиям:
без петель, удовлетворяющий
следующим условиям:
1. Существует только одна
вершина с нулевой степенью захода; эта
вершина называется источником
и обозначается через
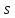 .
.
2. Существует только одна
вершина с нулевой степенью исхода; эта
вершина называется стоком
и обозначается через
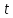 .
.
3. Каждой дуге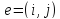 в сети
в сети
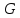 сопоставляется неотрицательное
вещественное число, называемое пропускной
способностью дуги
сопоставляется неотрицательное
вещественное число, называемое пропускной
способностью дуги
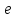 ;
оно обозначается через
;
оно обозначается через
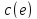 или
или
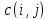 .
(Если не существует дуги, ориентированной
из
.
(Если не существует дуги, ориентированной
из
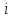 в
в
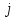 ,
то полагаем, что
,
то полагаем, что
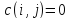 .)
.)
Моделью транспортной сети может служить водопроводная система, в которой сечения труб определяют пропускные способности соответствующих труб, т.е. количество жидкости. которое может пропустить труба за единицу времени.
Потоком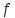 в транспортной сети
в транспортной сети
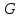 является функция, сопоставляющая каждой
дуге
является функция, сопоставляющая каждой
дуге
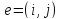 неотрицательное вещественное
число
неотрицательное вещественное
число
 так, что выполняются следующие условия:
так, что выполняются следующие условия:
1.
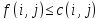 для любой дуги
для любой дуги
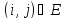 ;
;
2.
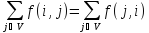 для любого
для любого
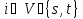 .
.
(Требование 2 − это условие сохранения баланса. Образно говоря, ″сколько втекает в вершину, столько и вытекает из неё″.)
Величина потока
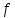 обозначается через
обозначается через
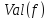 и определяется выражением
и определяется выражением
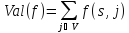 .
.
Говорят, что поток
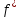 максимален,
если не существует потока
максимален,
если не существует потока
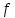 такого, что
такого, что
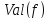 >
>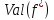 .
.
Постановка задачи. Найти максимальный поток в заданной транспортной сети.
Пусть
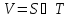 ,
,
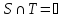 .
Разрез
.
Разрез
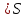 ,
,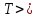 определяется как
множество дуг
определяется как
множество дуг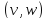 ,
у которых начало и конец лежат в разных
подмножествах
,
у которых начало и конец лежат в разных
подмножествах
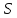 и
и
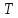 .
Разрез состоит из прямых
дуг, ориентированных из
.
Разрез состоит из прямых
дуг, ориентированных из
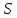 в
в
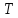 ,
и обратных
дуг, ориентированных из
,
и обратных
дуг, ориентированных из
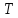 в
в
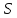 .
Если
.
Если
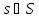 ,
,
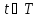 ,
то соответствующий разрез называется
(
,
то соответствующий разрез называется
(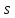 -
-
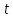 )
- разрезом.
См. рис. 1.
)
- разрезом.
См. рис. 1.
Далее рассматриваются только
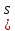 -
-
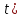 - разрезы.
- разрезы.
Пропускная способность
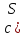 ,
,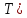 разреза
разреза
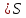 ,
,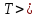 определяется как
сумма пропускных способностей прямых
дуг разреза. Разрез, пропускная способность
которого не больше, чем у любого другого
разреза, называется минимальным.
(В транспортной сети может быть несколько
минимальных разрезов, конечно, с
одинаковыми пропускными способностями.)
определяется как
сумма пропускных способностей прямых
дуг разреза. Разрез, пропускная способность
которого не больше, чем у любого другого
разреза, называется минимальным.
(В транспортной сети может быть несколько
минимальных разрезов, конечно, с
одинаковыми пропускными способностями.)
Поток из
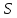 в
в
 определяется как
определяется как

Аналогично определяется
поток из
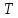 в
в
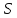 :
:
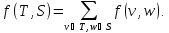
1. Лемма.
Для любого
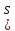 -
-
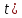 - разреза <
- разреза <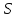 ,
,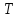 >
имеет место равенство
>
имеет место равенство
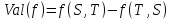 .
.
Доказательство.
Для
фиксированного
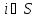 имеем
имеем
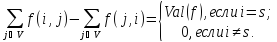
Суммируя
по всем
 ,
получаем
,
получаем
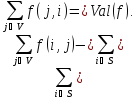
С другой стороны,
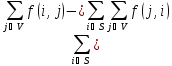

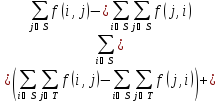
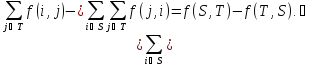
2. Следствие.
Для любого потока
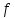 и любого
и любого
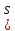 -
-
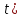 - разреза <
- разреза <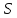 ,
,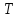 >
>
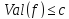 (
(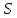 ,
,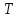 ).
).
Доказательство.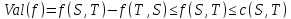 .
∎
.
∎
Для потока
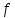 и разреза <
и разреза <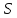 ,
,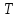 >
прямую дугу
>
прямую дугу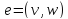 ,
где
,
где
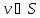 ,
,
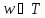 ,
будем называть
,
будем называть
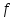 -насыщенной
(соответственно,
-насыщенной
(соответственно,
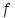 -не
-не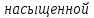 ),
если
),
если
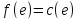 (соответственно, если
(соответственно, если
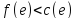 ).
Обратную дугу
).
Обратную дугу
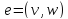 ,
где
,
где
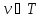 ,
,
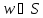 ,
будем называть
,
будем называть
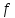 -нулевой
(соответственно,
-нулевой
(соответственно,
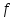 -положительной),
если
-положительной),
если
 (соответственно, если
(соответственно, если
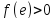 ).
).
3. Лемма.
Если величина потока
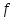 равна пропускной способности некоторого
разреза
равна пропускной способности некоторого
разреза
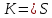 ,
,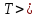 ,
то
,
то
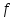 −
максимальный поток, а
−
максимальный поток, а
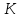 −
минимальный разрез. Для данного разреза
прямые дуги являются насыщенными, а
обратные −
нулевыми.
−
минимальный разрез. Для данного разреза
прямые дуги являются насыщенными, а
обратные −
нулевыми.
Доказательство.
Пусть
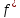 −
максимальный поток, а
−
максимальный поток, а
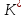 −
минимальный разрез. Так как
−
минимальный разрез. Так как
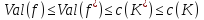 и,
по условию,
и,
по условию,
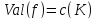 ,
то
,
то
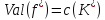 .
∎
.
∎
Рассмотрим в транспортной
сети цепочку
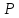 рёбер
рёбер
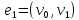 ,
,
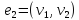 ,
, ,
,
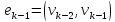 ,
,
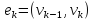 ,
,
соединяющую источник
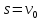 и некоторую вершину
и некоторую вершину
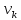 .
Заметим, что рёбра получаются из дуг
путём снятия ориентации. Соответствующие
дуги, составляющие цепочку, могут быть
как прямыми, т.е. ориентированными из
.
Заметим, что рёбра получаются из дуг
путём снятия ориентации. Соответствующие
дуги, составляющие цепочку, могут быть
как прямыми, т.е. ориентированными из
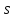 в
в
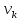 ,
так и обратными, т.е. ориентированными
из
,
так и обратными, т.е. ориентированными
из
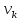 в
в
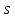 .
.
Для ребра
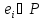 полагаем
полагаем
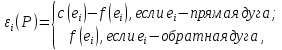
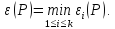
Цепочка
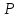 называется
называется
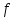 -ненасыщенной,
если
-ненасыщенной,
если
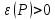 .
.
 -ненасыщенная
цепочка
из
-ненасыщенная
цепочка
из
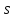 в
в
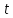 называется
называется
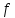 -дополняющей.
-дополняющей.
Наличие в сети
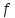 -дополняющей
цепочки
-дополняющей
цепочки
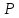 позволяет увеличить величину потока,
вводя новый поток
позволяет увеличить величину потока,
вводя новый поток
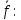
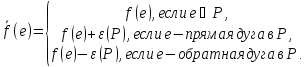
При этом
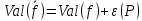 .
.
4. Теорема.
Поток
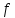 в транспортной сети максимален тогда
и только тогда, когда в сети отсутствуют
в транспортной сети максимален тогда
и только тогда, когда в сети отсутствуют
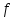 -дополняющие
цепочки.
-дополняющие
цепочки.
Доказательство.
Необходимость.
Если
поток максимален, то в сети заведомо
нет
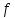 -дополняющих
цепочек.
В противном случае можно было бы построить
новый поток
-дополняющих
цепочек.
В противном случае можно было бы построить
новый поток
 ,
величина которого больше, чем у потока
,
величина которого больше, чем у потока
 .
.
Достаточность.
Предположим, что сеть с потоком
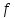 не содержит
не содержит
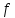 -дополняющих
цепочек.
Покажем, что в этом случае
-дополняющих
цепочек.
Покажем, что в этом случае
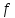 −
максимальный поток.
−
максимальный поток.
Разобьём
множество
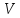 вершин сети на два непересекающихся
подмножества
вершин сети на два непересекающихся
подмножества
 и
и
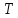 :
в
:
в
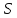 включим
те вершины
включим
те вершины
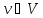 ,
до которых существуют
,
до которых существуют
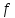 -ненасыщенные
цепочки
из источника
-ненасыщенные
цепочки
из источника
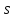 ,
а в
,
а в
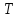 включим остальные вершины, т.е.
включим остальные вершины, т.е.
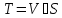 .
Очевидно, что
.
Очевидно, что
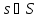 .
.
Пусть
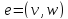 −
произвольная дуга разреза
−
произвольная дуга разреза
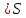 ,
,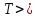 .
Если
.
Если
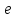 − прямая
дуга, т.е.
− прямая
дуга, т.е.
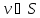 ,
,
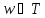 ,
то
,
то
 является
является
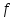 -насыщенной
дугой, поскольку иначе существует
-насыщенной
дугой, поскольку иначе существует
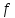 -ненасыщенная
цепочка
из
-ненасыщенная
цепочка
из
 в
в
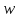 и
и
 .
Аналогично,
если
.
Аналогично,
если
 − обратная
дуга, т.е.
− обратная
дуга, т.е.
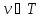 ,
,
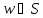 ,
то
,
то
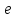 является
является
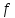 -нулевой
дугой
-нулевой
дугой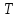 .
Таким
образом,
.
Таким
образом,
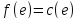 для прямых дуг и
для прямых дуг и
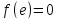 для обратных дуг разреза <
для обратных дуг разреза <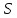 ,
, >.
Тогда
>.
Тогда
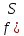 ,
,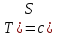 ,
,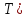 ,
,
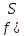 ,
,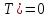 и
и
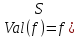 ,
,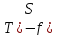 ,
,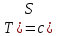 ,
, .
Из леммы 3 вытекает, что <
.
Из леммы 3 вытекает, что < ,
,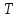 >
− минимальный
разрез, а
>
− минимальный
разрез, а
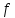 −
максимальный поток.∎
−
максимальный поток.∎
5. Следствие (теорема Форда-Фалкерсона). Величина максимального потока в транспортной сети равна пропускной способности минимального разреза.
ПОМЕЧАЮЩИЙ АЛГОРИТМ ФОРДА-ФАЛКЕРСОНА НАХОЖДЕНИЯ МАКСИМАЛЬНОГО ПОТОКА В ТРАНСПОРТНОЙ СЕТИ
Алгоритм основан на теореме 4 и состоит из двух фаз.
На первой фазе, используя
помечающую процедуру, устанавливаем,
существует ли в сети
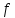 -дополняющая
цепочка.
Если такой цепочки нет, то согласно
теореме 4 поток в сети максимален (конец
алгоритма). В противном случае переходим
ко второй фазе, в которой, используя
метки, полученные на первой фазе, строим
новый поток
-дополняющая
цепочка.
Если такой цепочки нет, то согласно
теореме 4 поток в сети максимален (конец
алгоритма). В противном случае переходим
ко второй фазе, в которой, используя
метки, полученные на первой фазе, строим
новый поток
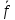 такой, что
такой, что
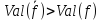 .
Фазы 1 и 2 повторяются до тех пор, пока
не будет построен максимальный поток.
.
Фазы 1 и 2 повторяются до тех пор, пока
не будет построен максимальный поток.
Метка, которую может получить
вершина
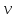 на фазе 1, имеет вид (
на фазе 1, имеет вид ( ,
,
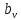 ,
,
 ),
где символ
),
где символ
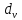 указывает на вершину, от которой получена
метка,
указывает на вершину, от которой получена
метка,
 указывает направление помечивания −
прямое (
указывает направление помечивания −
прямое (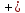 )
или обратное (
)
или обратное (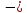 ),
наконец,
),
наконец,
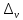 =
=
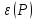 ,
если существует
,
если существует
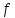 -ненасыщенная
цепочка
-ненасыщенная
цепочка
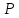 из
из
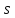 в
в
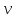 .
.
Помечивание начинается с пометки источника, который получает метку
 ,
,
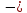 ,
,
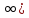 ,
где значение
,
где значение
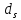 несущественно. Помечивание остальных
вершин происходит по следующим правилам.
несущественно. Помечивание остальных
вершин происходит по следующим правилам.
Прямое помечивание.
Если
 ,
то прямое помечивание
,
то прямое помечивание
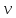 из
из
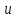 возможно, если вершина
возможно, если вершина
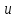 уже помечена и
уже помечена и
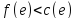 .
При этом вершина
.
При этом вершина
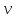 получает метку
получает метку
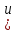 ,
,
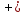 ,
,
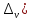 ,
где
,
где
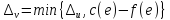 .
.
Обратное помечивание.
Если
 ,
то обратное помечивание
,
то обратное помечивание
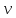 из
из
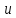 возможно, если вершина
возможно, если вершина
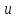 уже помечена и
уже помечена и
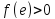 .
При этом вершина
.
При этом вершина
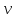 получает метку
получает метку
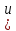 ,
,
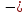 ,
,
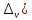 ,
где
,
где
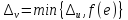 .
.
Фаза 1 завершается, если либо
1) вершина (сток)
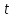 помечена, либо 2) вершина
помечена, либо 2) вершина
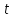 не помечена и ни одну из непомеченных
вершин не удаётся (нельзя) пометить. В
пределах фазы каждая вершина помечается
лишь один раз.
не помечена и ни одну из непомеченных
вершин не удаётся (нельзя) пометить. В
пределах фазы каждая вершина помечается
лишь один раз.
Если сток
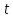 получил метку в первой фазе, то из правил
помечивания следует, что в сети существует
получил метку в первой фазе, то из правил
помечивания следует, что в сети существует
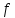 -дополняющая
цепочка
-дополняющая
цепочка
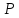 и
и
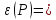
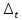 >0.
Во второй фазе эта цепочка прослеживается
в обратном направлении (начиная с
>0.
Во второй фазе эта цепочка прослеживается
в обратном направлении (начиная с
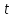 )
с помощью символов
)
с помощью символов
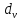 ,
что позволяет построить новый поток
,
что позволяет построить новый поток
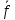 с
увеличенным значением
с
увеличенным значением
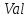 .
.
Алгоритм Форда-Фалкерсона.
Вход:
транспортная
сеть
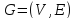 ,
заданная матрицей (
,
заданная матрицей (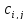 ),
где
),
где
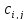 =
=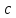 (
(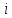 ,
,
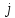 ),
),
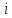 ,
,
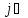
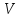 ,
пропускных способностей, или каким-нибудь
другим способом.
,
пропускных способностей, или каким-нибудь
другим способом.
(Начинаем с нулевого потока.)
for
 е
∈
E
do
f(e):=
0;
е
∈
E
do
f(e):=
0;
(Фаза 1.)
Удаляем все метки вершин;
Помечаем источник;
while вершина t не помечена и существует непомеченная вершина v do
помечаем вершину v;
od;
if сток не помечен then конец: максимальный поток построен;
(Фаза 2.)
v:= t; u:= dv;
while v ≠ s do
if bv = ″+″ then f(u,v):= f(u,v)+ ∆t
else f(u,v):= f(u,v)− ∆t;
v:= u
od;
Возврат на фазу 1.
Выход: максимальный поток f.
