Задачи для программирования по темам

″ТЕОРИЯ ГРАФОВ″, ″РЕКУРСИВНЫЕ ФУНКЦИИ″, ″МАШИНЫ ТЬЮРИНГА″

Направление ″бизнес-информатика″, специальность ″математические методы в экономике″

Вопросы:

1 . Обходы графа. Вычисление числа компонент связности графа.

2. Алгоритмы поиска путей в графе.

3. Алгоритмы нахождения минимального остова в графе.

4. Хроматическое число графа. Алгоритм правильной раскраски вершин графа методом перебора с возвратами.

5. Транспортные сети. Теорема Форда-Фалкерсона о максимальном потоке в транспортной сети.

6а. Варианты задач для групп по направлению ″Бизнес-информатика″. Тема ″Транспортные сети″

6б. Варианты задач для групп по специальности ″Математические методы в экономике″. Тема ″Транспортные сети″

7. Задачи по теме ″Рекурсивные функции″.

8. Задачи по теме ″Машины Тьюринга″.

1 . Обходы графа . Вычисление числа компонент связности графа.

Определение. Обход графа – это прохождение его вершин в некотором систематическом порядке.

Решение многих задач теории графов связано с организацией систематического обхода всех вершин графа. Существуют два наиболее часто используемых метода обхода графов: поиск в глубину и поиск в ширину.

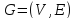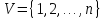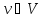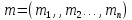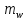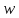Поиск в глубину ПВГ в графе с множеством вершин и множеством рёбер начинается с произвольной вершины . Для помечивания пройденных вершин используется массив , где − метка вершины , причём 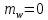, если 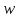− ещё не посещенная вершина, а − если уже посещенная. Для организации обхода используется стек 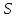, в вершину которого помещается текущая пройденная вершина.

Алгоритм ПВГ (, ) ≡ {

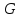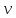S ← ∅; опустошаем стек

m_y ← 1; помечаем вершину v

S ⟸ v; помещаем вершину v в стек

while S ≠ ∅ do продолжаем обход, пока стек не пуст

a ⟸ S; извлекаем очередную вершину из стека

if существует ребро (a,b) ∈ E с непомеченной вершиной b

then {

S ⟸ a; возвращаем вершину a в стек

m_b ← 1; помечаем вершину b

S ⟸ b помещаем вершину b в стек

od

}.

Т.о., при поиске (обходе) в глубину после очередной посещённой вершины 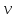посещается любая смежная с ней вершина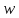. Если все вершины, смежные с 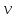, уже посещались, то происходит возврат к вершине 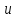, предыдущей по отношению к

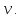
Поиск (обход) в ширину ПВШ отличается от ПВГ тем, что вначале посещаются вершины, смежные с исходной, затем смежные с посещёнными и т.д. Если считать, что смежные вершины находятся на расстоянии 1 друг от друга, то вначале посещаются вершины, находящиеся на расстоянии 1 от исходной, затем вершины, находящиеся на расстоянии 2, и т.д. Для реализации алгоритма требуется очередь .

Алгоритм ПВШ (, ) ≡ {

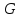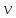Q ← ∅; опустошаем очередь

m_v ← 1; помечаем вершину v

Q ⟸ v; помещаем вершину v в очередь

while Q ≠ ∅ do продолжаем обход, пока очередь не пуста

a ⟸ Q; извлекаем очередную вершину из очереди

while существует ребро (a,b) ∈ E с непомеченной вершиной b

do

m_b ← 1; помечаем вершину b

Q ⟸ b помещаем вершину b в очередь

od

od}.

Определение. Максимальный связный подграф графа 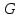называется компонентой связности графа . Несвязный граф состоит из нескольких компонент связности.

Пример использования обхода графа.

Алгоритм вычисления k − числа компонент связности графа:

k ← 0;

for v ← 1 to n do m_v ← 0;

for v ← 1 to n do {

if m_v = 0 then {s ← s + 1; ПВГ (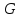, ) или ПВШ (, ) }.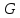
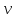