4.3. Система двох випадкових величин.

Двовимірною називають випадкову величину , можливі значення якої є пари чисел . Складові і , які розглядаються одночасно, утворюють систему двох випадкових величин.

Двовимірну величину геометрично можна тлумачити як випадкову точку на площині , або як випадковий вектор .

Дискретною називають двовимірну величину, складові якої дискретні. Неперервною називають двовимірну величину, складові якої неперервні.

Законом розподілу ймовірностей двовимірною випадкової величини називають відповідність між можливими значеннями та їх ймовірностями.

Функцією розподілу ймовірностей двовимірною випадкової величини називають функцію , яка визначає для кожної пари чисел ймовірність того, що прийме значення, менше ніж , і при цьому прийме значення, менше ніж :

. (4.13)

Геометрично цю рівність можна тлумачити так: є ймовірність того, що випадкова точка потрапить в нескінчений квадрант з вершиною , який розташований лівіше на нижче цієї вершини.

Функція розподілу має наступні властивості:

1) ;

2) , якщо ,

, якщо .

3) ; ;

; .

4) ,

.

Використовуючи функцію розподілу, можна знайти ймовірність попадання випадкової точки в прямокутник , :

.

Щільністю сумісного розподілу ймовірностей (двовимірною щільністю ймовірностей) неперервної двовимірної випадкової величини називають другу змішану похідну від функції розподілу:

. (4.14)

Знаючи щільність розподілу, можна знайти функцію розподілу за формулою

. (4.15)

Ймовірності попадання випадкової точки в область визначається рівністю:

(4.16)

Двовимірна щільність розподілу має наступні властивості:

1) ;

2) .

Нехай складові і дискретні і мають відповідно наступні можливі значення: ; . Умовним розподілом складової при ( зберігає одне й те саме значення при всіх можливих значеннях ) називають сукупність умовних ймовірностей

, , ..., .

Аналогічно визначається умовний розподіл .

Умовні ймовірності складових і обчислюють відповідно за формулами

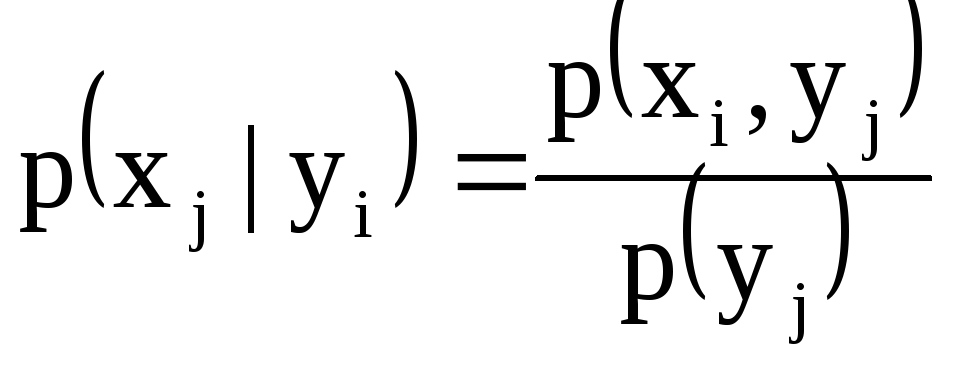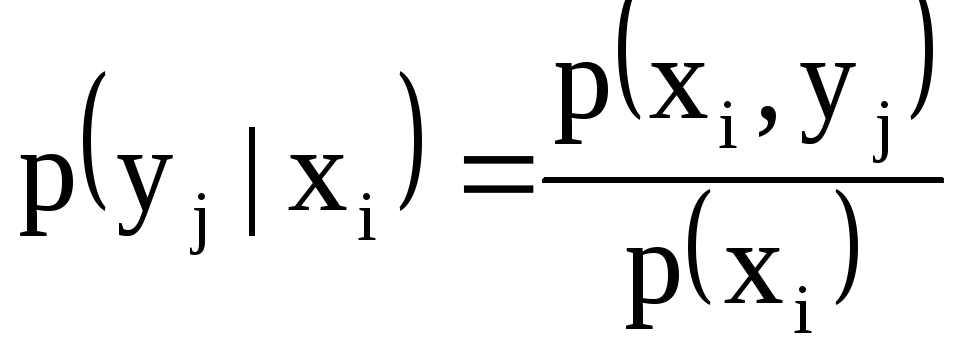; . (4.17)

Для контролю обчислень доцільно переконатися, що сума ймовірностей умовного розподілу дорівнює одиниці.

Якщо складові і неперервні, щільність розподілу однієї зі складових дорівнює невласному інтегралу з нескінченими границями від щільності сумісного розподілу системи, причому змінна інтегрування відповідає другій складовій:

; . (4.18)

Умовною щільністю розподілу складової при заданому значенні називають відношення щільності сумісного розподілу системи до щільності розподілу складової :

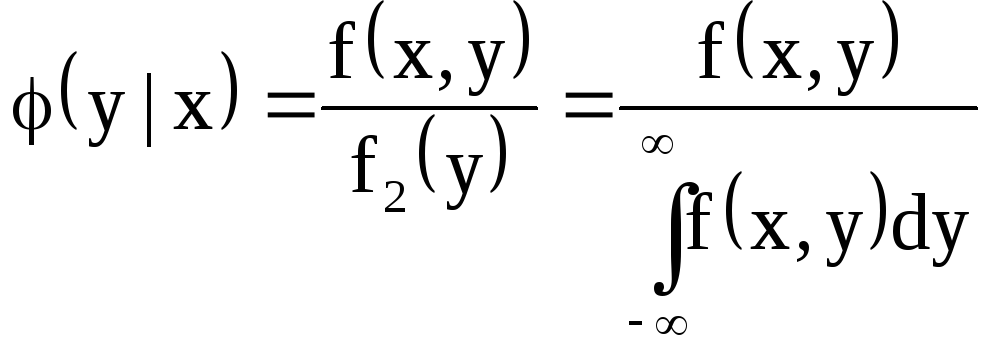. (4.19)

Аналогічно визначається умовна щільність розподілу складової :

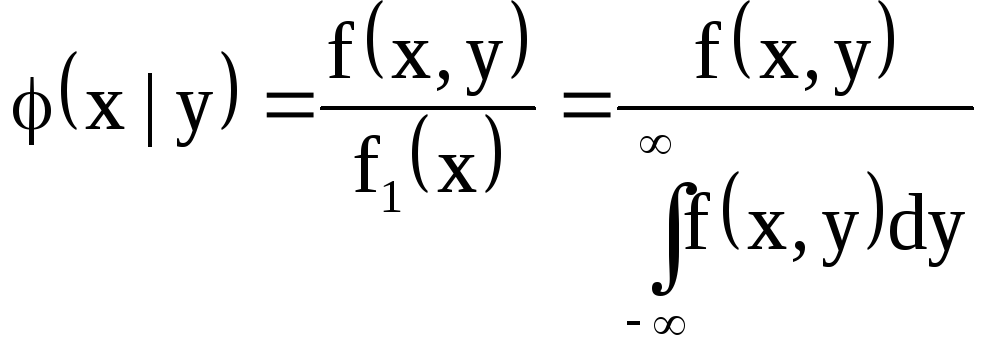. (4.20)

Якщо умовні щільності розподілу випадкових величин і дорівнюють їх безумовним щільностям, то такі величини незалежні.

Рівномірним називають розподіл двовимірної неперервної випадкової величини , якщо в області, якої належать можливі значення , щільність сумісного розподілу ймовірностей зберігає постійне значення.

Знаючи щільності розподілів складових і неперервної двовимірної випадкової величини , можна знайти їх математичне сподівання і дисперсії:

; ; (4.21)

; (4.22)

; (4.23)

Іноді зручніше використовувати формули, які містять двовимірні щільності ймовірностей (подвійні інтеграли беруться по області можливих значень системи):

; ; (4.24)

; (4.25)

; (4.26)

Початковим моментом порядку системи називають математичне сподівання добутку :

(4.27)

Центральним моментом порядку системи називають математичне сподівання добутку відхилень відповідно -го та -го степенів:

. (4.28)

Кореляційним моментом системи називають центральний момент порядку 1+1:

. (4.29)

Коефіцієнтом кореляції величин і називають відношення кореляційного моменту до добутку середніх квадратичних відхилень цих величин:

. (4.30)

Коефіцієнт кореляції - безрозмірна величина, причому . Коефіцієнт кореляції служить для оцінки тісноти лінійного зв’язку між і : чим ближче абсолютна величина коефіцієнта кореляції до одиниці, тим зв’язок сильніше; чим ближче абсолютна величина коефіцієнта кореляції до нуля, тим зв’язок слабше.

Корельованими називають дві випадкові величини, якщо їх кореляційний момент не рівний нулю.

Некорельованими називають дві випадкові величини, якщо їх кореляційний момент дорівнює нулю.

Дві величини, які є корельованими також є залежними; якщо дві величини залежні, то вони можуть бути як корельованими, так і некорельованими.

Для неперервних величин і кореляційний момент може бути знайдений за формулами:

; (4.31)

. (4.32)