Розділ 2. Транспортна задача. Найпростіші задачі на мережах

§ 2.1. Транспортна задача. Основні властивості

Математична модель транспортної задачі (ТЗ) уже розглядалася нами в попередньому параграфі, як приклад задачі лінійного програмування.

Так звана збалансована ТЗ у математичній постановці має вигляд

, (2.1.1)

(2.1.2)

, , . (2.1.3)

. (2.1.4)

Тут – об’єм запасу продукту в пункті постачання (виробництва) , – потреба у цьому продукті в пункті споживання , – питомі затрати по перевезенню продукту із в , а – запланований об’єм перевезень із пункту постачання в пункт споживання . Умова (2.1.4) є так званою умовою збалансованості та означає, що сумарний об’єм запасів продукту в пунктах постачання (виробництва) збігається із сумарним об’ємом потреб у продукті в пунктах споживання .

Якщо задача не є збалансованою (умова (2.1.4) не виконується), то легко перейти до розширеної збалансованої задачі, ввівши в розгляд збалансовуючі змінні.

Наприклад, якщо сумарний об’єм запасів перевищує об’єм потреб , то вводять у розгляд додатковий (фіктивний) пункт споживання із потребою і збалансовуючі невід’ємні змінні , які не входять у цільову функцію.

Умови (2.1.2) і (2.1.3) набувають при цьому вигляду

, , .

Замість нерівності отримуємо умову збалансованості

.

Якщо ж сумарний об’єм запасів менший від сумарного об’єму потреб , то поступають аналогічно, вводячи в розгляд додатковий (фіктивний) пункт постачання із запасом та відповідні невід’ємні збалансовуючі змінні .

Умови (2.1.2) і (2.1.3) набувають при цьому вигляду

, , ,

а умова збалансованості –

.

Після розв’язування збалансованої задачі розв’язок початкової незбалансованої задачі легко визначити, відкинувши з отриманого розв’язку компоненти, відповідні значенням збалансовуючих змінних.

В подальшому ми будемо вважати, що задається збалансована задача (2.1.1) – (2.1.4), навіть не виписуючи умови (2.1.4).

Звичайно, ця задача є задачею лінійного програмування і може бути розв’язана за допомогою вже відомих нам симплексного чи двоїстого симплексного методів.

Правда, істотною завадою на цьому шляху є велика розмірність задачі – кількість змінних дорівнює , матриця непрямих умов (2.1.2) розмірності . Проте специфічна риса цієї матриці те, що її елементами є лише одиниці і нулі та матриця є “розрідженою” (переважна більшість її елементів дорівнює нулю). Останнє може суттєво допомогти при розв’язуванні задачі. Зокрема, відповідна до (2.1.1) – (2.1.3) задача записується у вигляді

, (2.1.5)

, , . (2.1.6)

Виписавши матрицю обмежень (2.1.2), не важко переконатися, що її ранг дорівнює . Це означає, що одне рівняння з непрямих обмежень є лінійною комбінацією інших рівнянь (наслідок збалансованості) і що базисний (опорний) план задачі містить не більше ніж відмінних від нуля компонент.

Отже, невироджений базисний план перевезень містить рівно компонент, більших від нуля.

Зрозуміло також, що об’єм перевезень із пункту постачання в пункт споживання , не може перевищувати меншого із двох чисел та , тобто

.

Це означає, що множина допустимих планів ТЗ обмежена і цільова функція задачі завжди обмежена знизу.

Легко переконатися також у тому, що множина допустимих планів збалансованої транспортної задачі не порожня.

Дійсно, числа , , невід’ємні і задовольняють умови (2.1.2)

,

.

Таким чином, ми приходимо до висновку, що розв’язок збалансованої ТЗ завжди існує.

Двоїсті змінні називаються потенціалами пунктів постачання, а – потенціалами пунктів споживання. Якщо ввести позначення

, , ,

то другу теорему двоїстості (Твердження 1.7.4) для задачі (2.1.1) – (2.1.3) можна сформулювати так:

базисний невироджений план перевезень

є оптимальним планом тоді і тільки тоді, якщо існують та , такі, що

для , (2.1.7)

для . (2.1.8)

Ми вважатимемо, що завжди працюємо з базисними невиродженими планами. Таке обмеження не принципове, бо існують методи запобігання виродженості. З ними можна ознайомитись, наприклад, в [11]. Всі дані задачі (2.1.1) – (2.1.3) можна записати у вигляді таблиці

Пункти споживання Пункти постачання			…		Запаси
			…
			…
…	…	…	…	…	…
			…
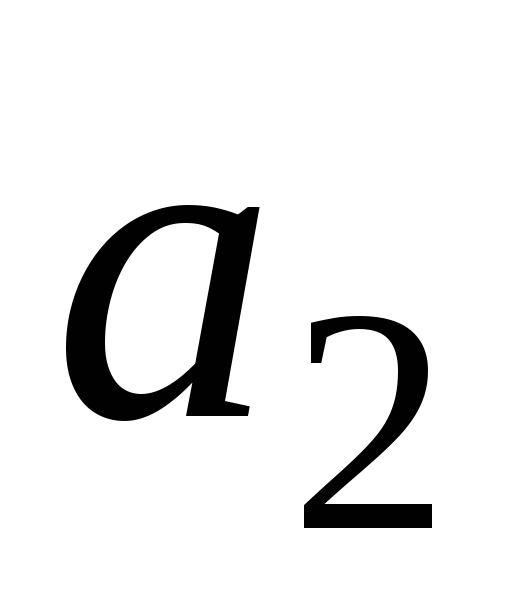
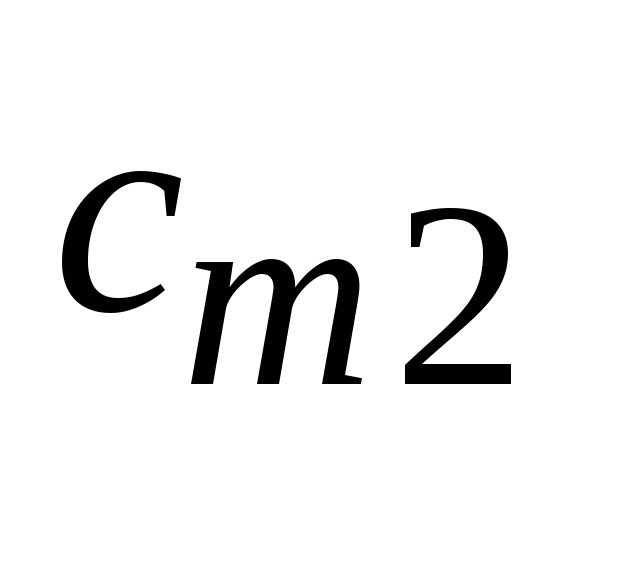
Потреби			…

При розв’язуванні задачі в клітинки -го рядка та -го стовпця вписують компоненти допустимого плану. Якщо , то відповідну клітинку таблиці не заповнюють нулем і називають її порожньою.

Наприклад, таблиця може мати вигляд

10	2	15	1	5	3			3		30
	1		4	20	2			1		20
	3		2	5	2		20	1		25
10		15		30		20			75

Аналізуючи наведені дані таблиці, робимо висновок, що план

допустимий. Відповідні затрати легко обчислити

.

У системі обмежень-рівностей (2.1.2) вектор-стовпчик, відповідний змінній , має вигляд

.

Одиниці дорівнюють лише компоненти з номерами та , всі інші компоненти дорівнюють нулю. У зв’язку з цим лінійна незалежність чи лінійна залежність векторів , відповідних ненульовим значенням компонент допустимого плану перевезень, еквівалентні неможливості чи можливості побудувати в таблиці замкнутий цикл.

Під замкнутим циклом (або просто – циклом) у таблиці розумітимемо замкнуту ламану з горизонтальними і вертикальними ланками, у вершинах якої знаходяться клітинки таблиці, заповнені ненульовими значеннями компонент допустимого плану перевезень.

Можна довести

Твердження 2.1.1. Допустимий план перевезень

є базисним тоді і тільки тоді, коли у відповідній таблиці не можна побудувати замкнутого циклу.

Легко переконатись, що наведений вище план перевезень базисний.

Допустимий план

тієї ж задачі небазисний, бо у відповідній таблиці можна побудувати цикл.

10	2	10	1	0	3		10	3		30
	1		4	20	2			1		20
	3	5	2	10	2		10	1		25
10		15		30		20			75

Цей цикл зображено в таблиці. Вершинами циклу є клітини (1;2), (1;4), (3;2), (3;4). Перше число означає номер рядка, в якому знаходиться клітинка таблиці, а друге – номер стовпчика.

Опираючись на сказане вище, ми можемо гарантувати, що допустимий план перевезень є базисним невиродженим планом транспортної задачі, якщо він містить рівно ненульових компонент і у відповідній таблиці не можна побудувати замкнутого циклу.

Потенціали пунктів постачання і пунктів споживання, поняття циклу, поняття базисного плану перевезень відіграватимуть важливу роль при побудові методу розв’язування ТЗ.

Цей метод враховує специфіку задачі, істотно відрізняється від загальних симплексного чи двоїстого симплексного методів. Проте, цей метод, як і згадані вище загальні методи, має ітераційний характер і дозволяє від неоптимального базисного плану переходити до іншого базисного плану, на якому значення цільової функції (значення затрат на перевезення) менше, ніж на попередньому плані.