§ 1.7. Двоїстість у лінійному програмуванні

У лінійному програмуванні корисним є поняття двоїстості або, як його ще називають, спряженості.

За допомогою цього поняття вдається глибше вивчити властивості ЗЛП, отримати нові критерії оптимальності, побудувати нові методи розв’язування ЗЛП, оцінити вплив параметрів задачі на значення цільової функції.

Почнемо з розгляду деякої СЗЛП

, (1.7.1)

(1.7.2)

, ,...,. (1.7.3)

Двоїстою (спряженою) задачею лінійного програмування до задачі (1.7.1) – (1.7.3) назвемо задачу

, (1.7.4)

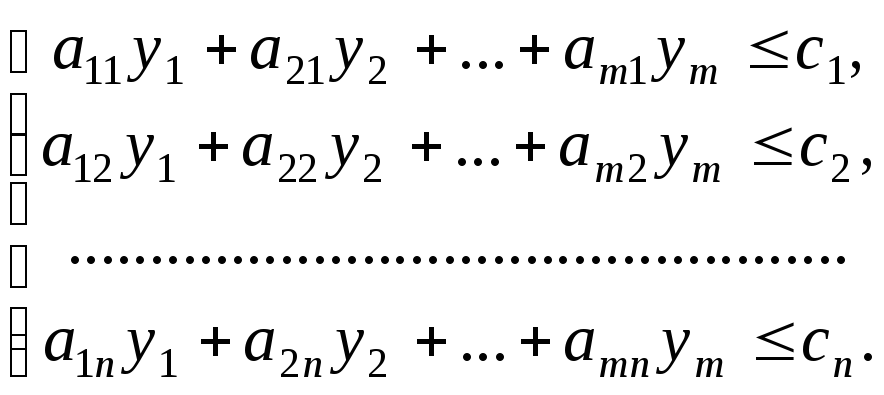(1.7.5)

Окреслимо характерні властивості задачі (1.7.4) – (1.7.5):

а) кількість змінних дорівнює кількості непрямих обмежень (1.7.2) початкової задачі;

б) кількість непрямих обмежень (1.7.5) збігається з кількістю змінних у задачі (1.7.1) – (1.7.3);

в) на змінні не накладаються прямі обмеження по знаку;

г) задача (1.7.4) – (1.7.5) не є стандартною.

Зазначимо також, що при побудові двоїстої до задачі (1.7.1) – (1.7.3), коефіцієнти та міняються ролями, задача мінімізації цільової функції замінюється задачею максимізації цільової функції , непрямі обмеження-рівності (1.7.2) замінюються обмеженнями-нерівностями (1.7.5).

Якщо СЗЛП (1.7.1) – (1.7.3) записати в матрично-векторній формі

,

, ,

то відповідна двоїста задача (1.7.4) – (1.7.5) у матрично-векторному варіанті набуде вигляду

,

,

де – матриця, утворена транспонуванням матриці .

Переходячи до мінімізації функції , добавивши у (1.7.5) невід’ємні збалансовуючі змінні та замінивши кожну зі змінних різницею двох невід’ємних змінних, легко отримаємо відповідну до (1.7.4) – (1.7.5) стандартну ЗЛП. Отримані обмеження-рівності зручно помножити на , що, взагалі кажучи, не змінює задачі.

Якщо для побудованої СЗЛП виписати відповідну двоїсту задачу, то вона матиме вигляд задачі (1.7.1) – (1.7.3). В цьому розумінні задачі (1.7.1) – (1.7.3) та (1.7.4) – (1.7.5) є взаємно двоїстими. Ці дві задачі називають несиметричною парою двоїстих задач.

Проілюструємо сказане на простому прикладі.

Нехай задана СЗЛП

, (1.7.6)

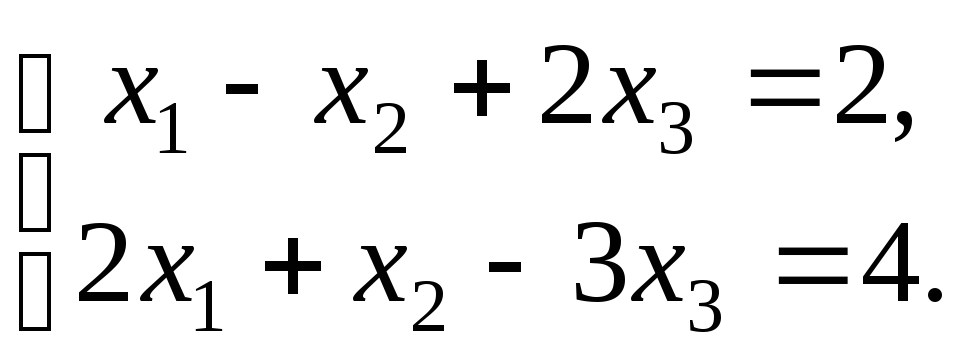(1.7.7)

, , . (1.7.8)

Згідно з визначенням, відповідною двоїстою задачею є задача

, (1.7.9)

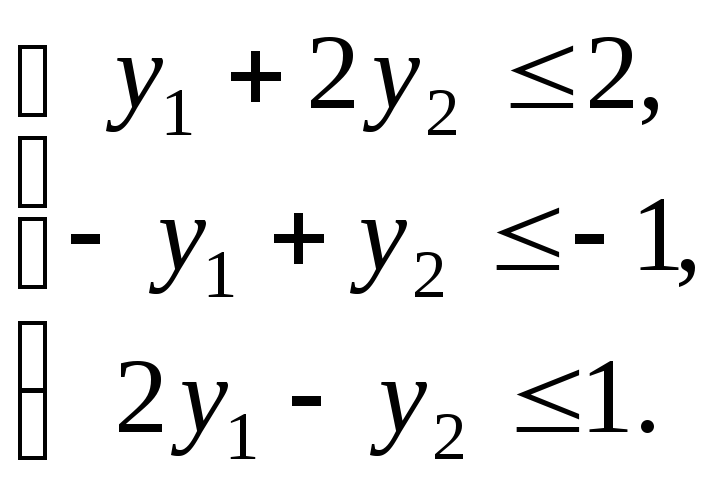(1.7.10)

Зведемо отриману задачу до стандартного вигляду. Нехай . Нехай також , , . Тоді (1.7.10) можна записати у вигляді

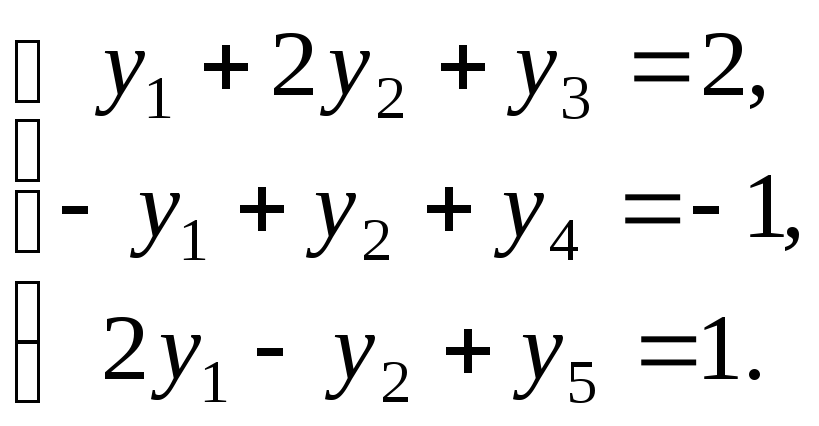
Замінимо тепер 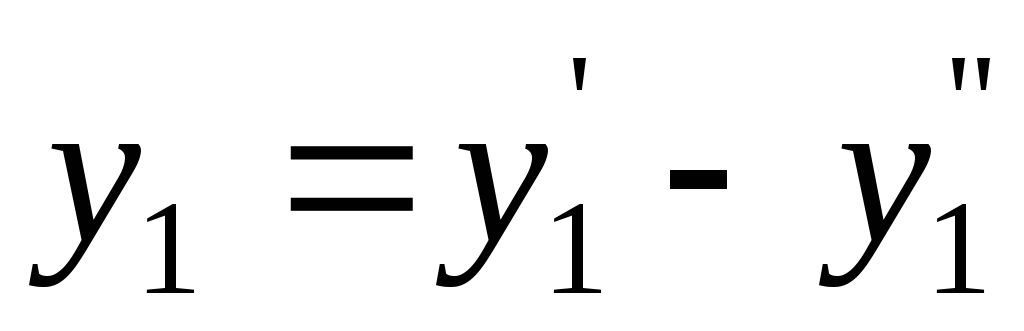, , 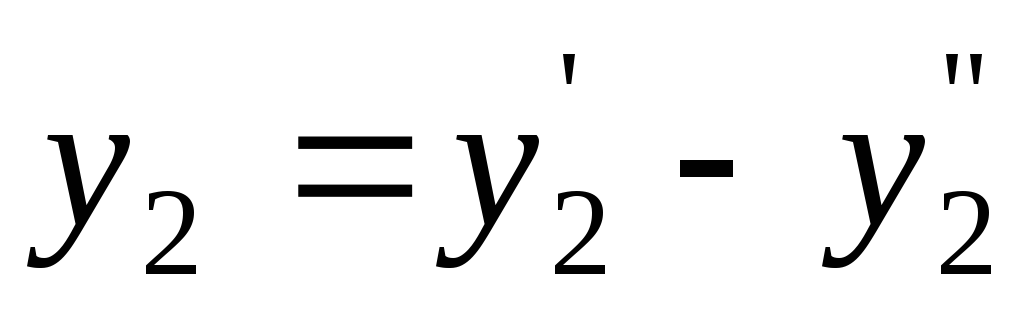де , , , 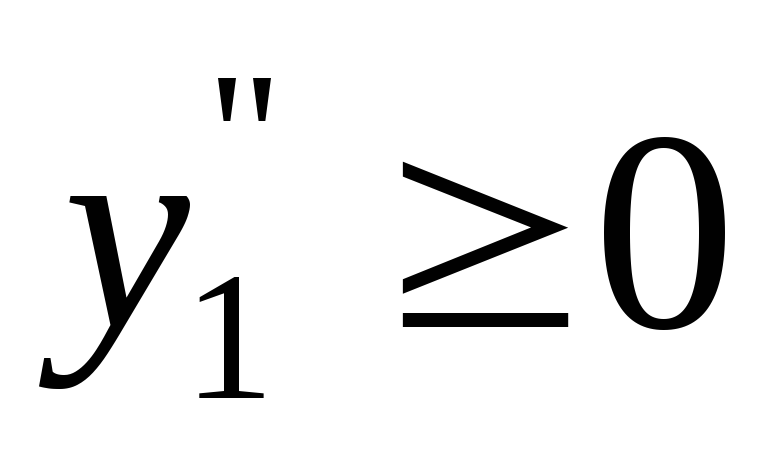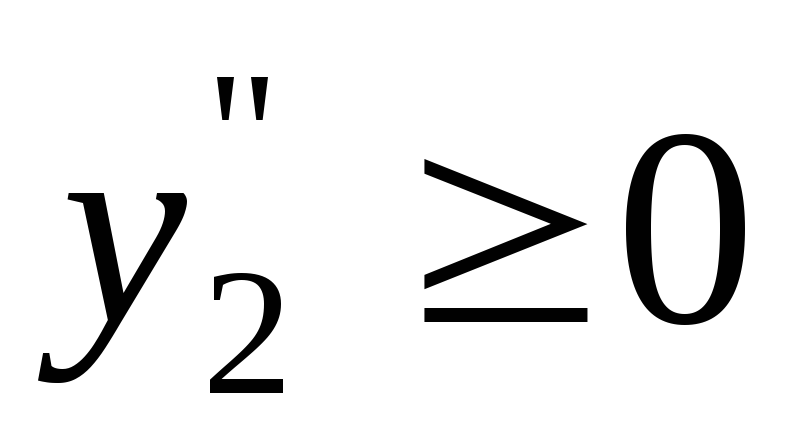. Отримуємо СЗЛП

,

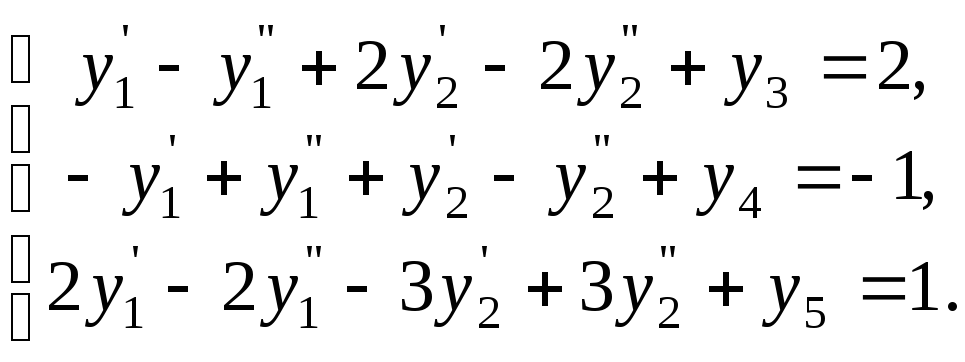(1.7.11)

, , , , , , .

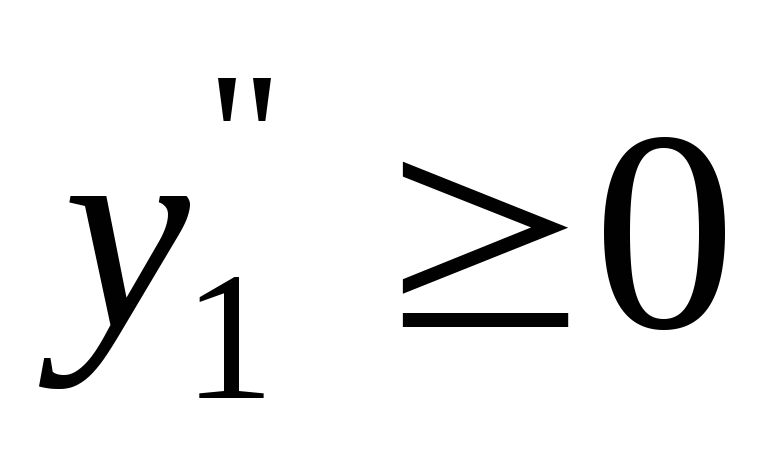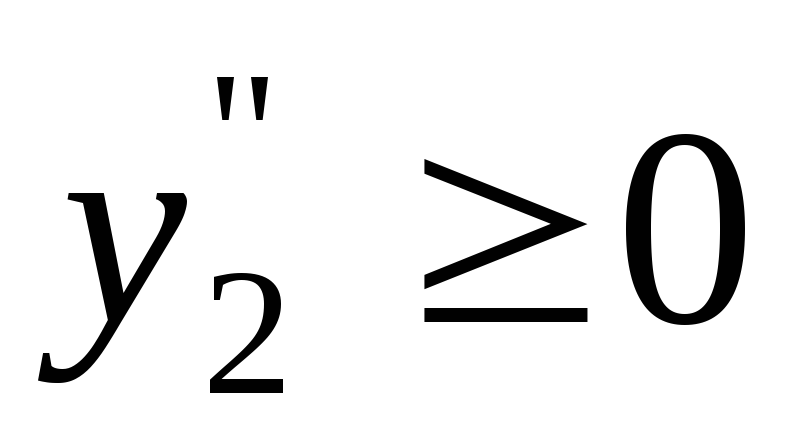Зауважимо, що змінні входять до з коефіцієнтами, які дорівнюють нулю.

Помножимо обмеження-рівності (1.7.11) на –1. Маємо СЗЛП

,

, , , , , , .

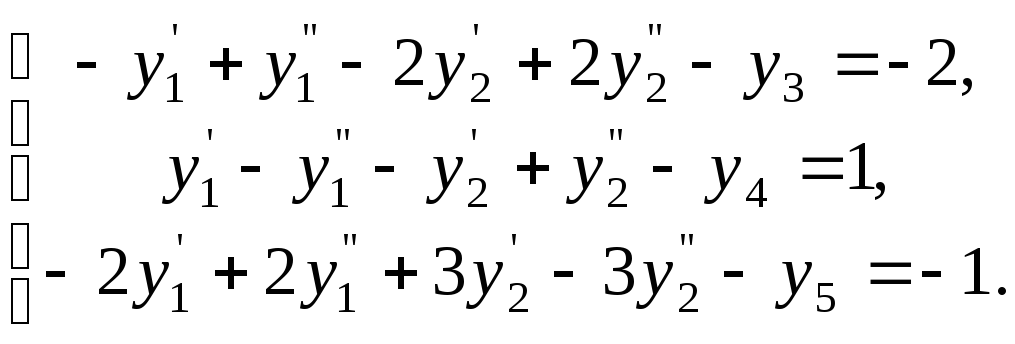
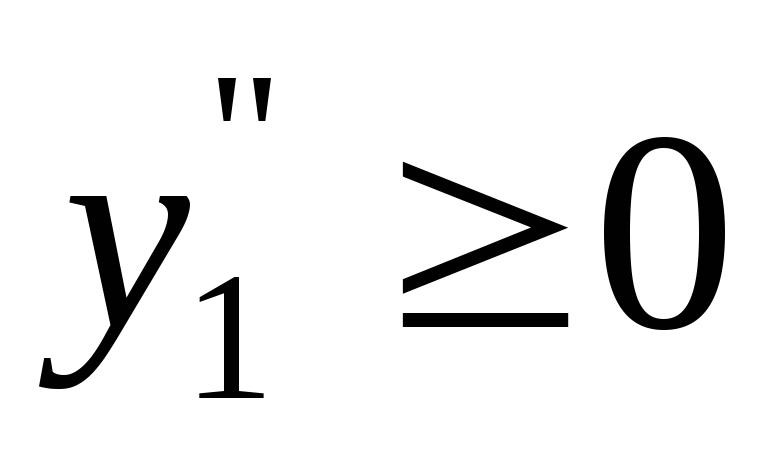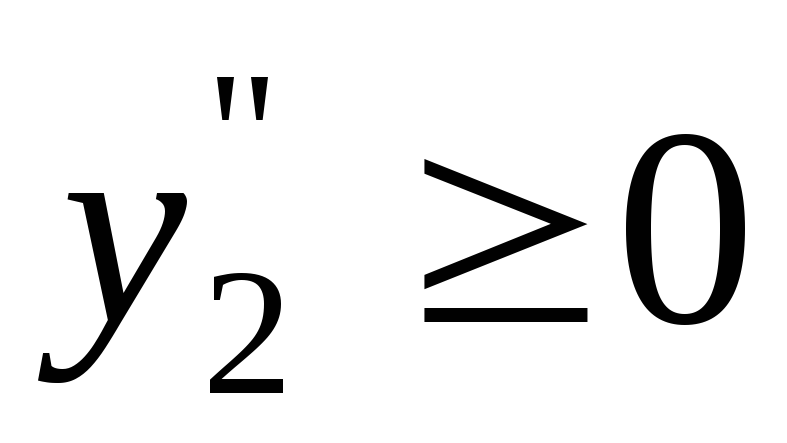Відповідна двоїста задача (її змінні позначимо ) набуває вигляду

,

або, як легко зрозуміти,

,

, ,.

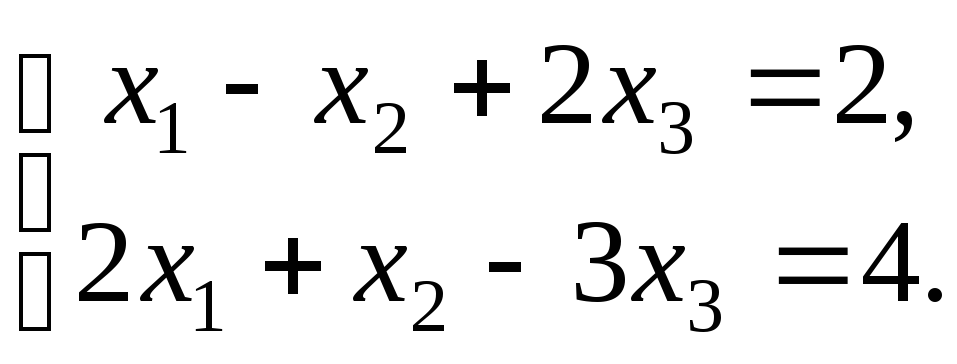
Ми отримали задачу (1.7.6) – (1.7.8). Отже, задачі (1.7.6) – (1.7.8) та (1.7.9) – (1.7.10) дійсно є взаємно двоїстими.

Зауваження. Якби ми не множили на рівності (1.7.11), то в результаті отримали б задачу

,

, , ,

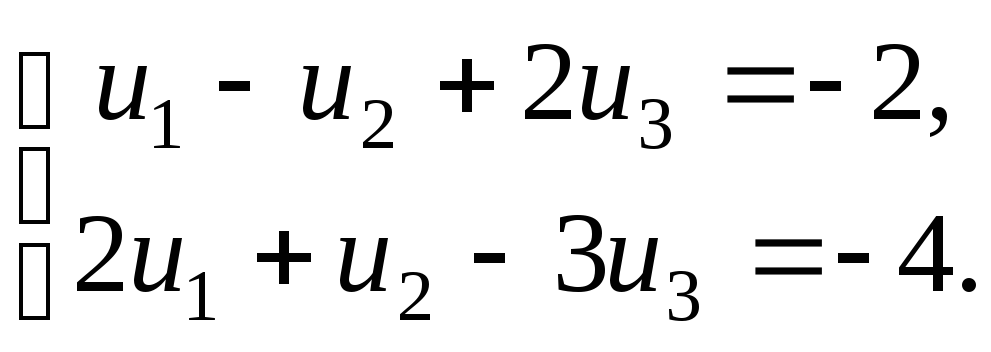
від якої легко перейти до отриманої раніше, зробивши заміну змінних , , .

Використовуючи зведення ЗЛП до СЗЛП, легко переконатися, що у випадку, коли початкова задача задана у вигляді

, (1.7.12)

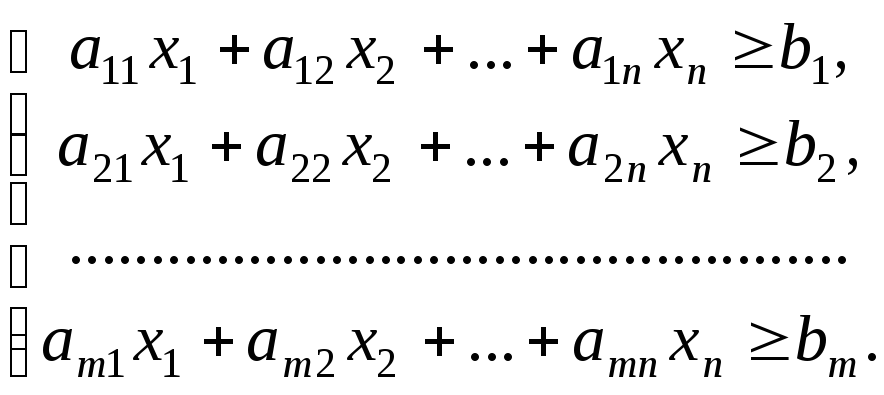(1.7.13)

, ,...,. (1.7.14)

то відповідна двоїста задача записується так:

, (1.7.15)

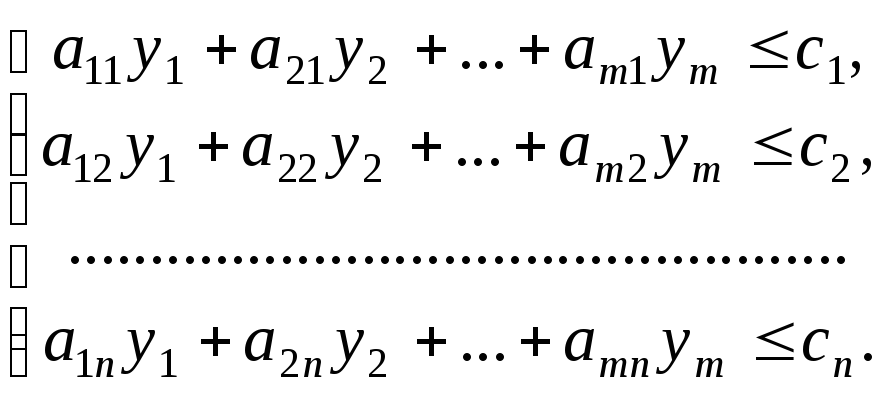(1.7.16)

, ,...,. (1.7.17)

Задачі (1.7.12) – (1.7.14) та (1.7.15) – (1.7.17) утворюють так звану симетричну пару простих задач.

У матрично векторному вигляді симетрична пара задач набуває вигляду

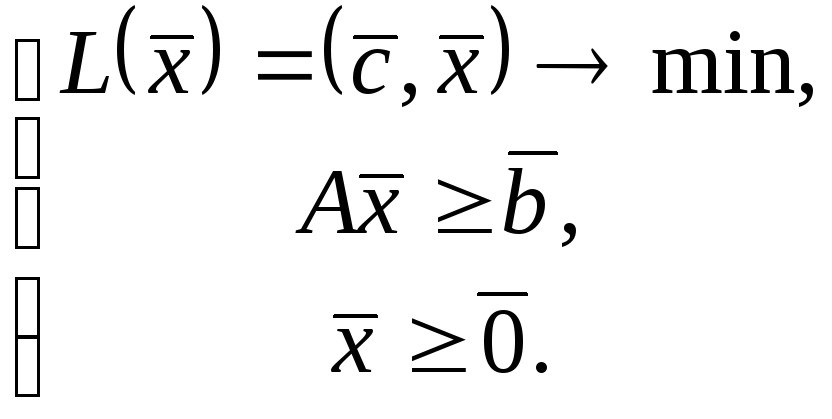
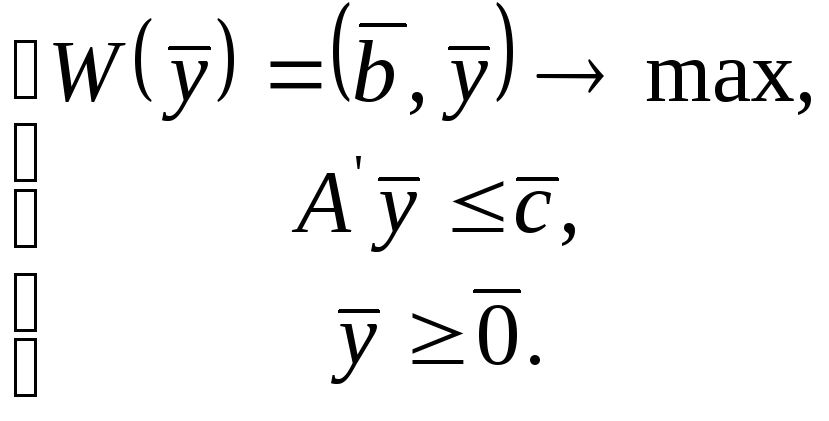
Ці задачі теж є взаємно двоїстими. В кожній із них на змінні накладаються прямі обмеження невід’ємності.

На двоїсті змінні обмеження невід’ємності не накладаються, якщо відповідне непряме обмеження на мало вигляд рівності.

Сформулюємо правила побудови двоїстої задачі до заданої загальної задачі лінійного програмування. Ми вважатимемо, що непрямі обмеження-нерівності у вихідній задачі мають вигляд .

1. Якщо у заданій (вихідній) ЗЛП мова йде про мінімізацію (максимізацію) цільової функції , то в двоїстій задачі необхідно максимізувати (мінімізувати) цільову функцію .

2. Кількість компонент вектора дорівнює кількості непрямих обмежень на компоненти вектора вихідної задачі. При цьому перша компонента відповідає першому за порядком непрямому обмеженню, друга – другому і т.д.

3. Коефіцієнти цільової функції стають вільними членами непрямих обмежень у двоїстій задачі, а вільні члени непрямих обмежень вихідної задачі – коефіцієнтами цільової функції двоїстої задачі.

4. Стовпці матриці непрямих обмежень вихідної задачі стають рядком матриці непрямих обмежень двоїстої задачі.

5. Якщо непряме обмеження за номером вихідної задачі має вигляд рівності, то на змінну двоїстої задачі не накладається умова невід’ємності. Якщо ж це обмеження має вигляд нерівності, то на накладається умова .

6. Якщо у вихідній задачі на не накладається умова , то непряме відповідне обмеження за номером у двоїстій задачі має вигляд рівності. Якщо ж на накладається обмеження , то відповідне непряме обмеження двоїстої задачі має вигляд нерівності типу “”.

Наприклад, якщо вихідна задача ЗЛП має вигляд

,

, ,,

то двоїстою є задача

,

,.

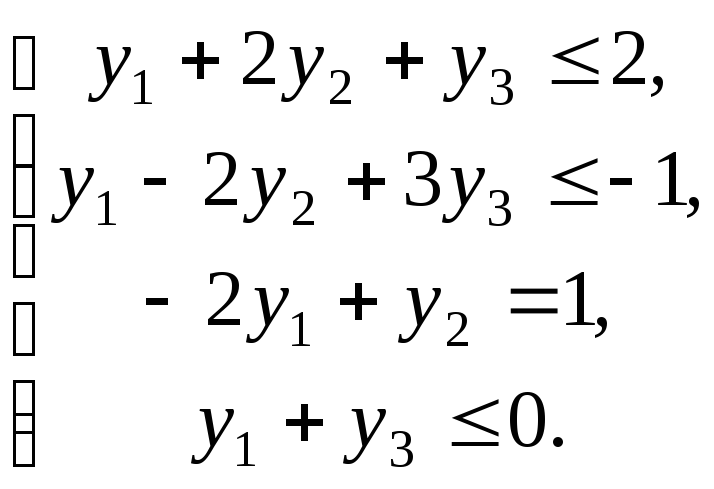
Важливість поняття двоїстої задачі в лінійному програмуванні підкреслюють так звані теореми двоїстості, до формулювання і обговорення яких ми перейдемо. Відповідні твердження ми сформулюємо для несиметричної пари двоїстих задач (1.7.1) – (1.7.3) та (1.7.4) – (1.7.5).

Твердження 1.7.1. Для всякого допустимого плану задачі (1.7.1) – (1.7.3) і всякого допустимого плану задачі (1.7.4) – (1.7.5) виконується нерівність .

Твердження 1.7.2. (перша теорема двоїстості, теорема існування). Якщо одна з пари двоїстих задач має розв’язок, то і друга задача має розв’язок. При цьому оптимальні значення цільових функцій та збігаються.

Якщо цільова функція однієї із пари двоїстих задач не обмежена (знизу – при мінімізації, зверху – при максимізації), то друга задача не має допустимих планів.

Твердження 1.7.3. Якщо для деякого допустимого плану вихідної задачі й деякого допустимого плану двоїстої їй задачі

,

то і є оптимальними планами (розв’язками) відповідних задач двоїстої пари.

Це твердження доповнює Твердження 1.7.1 і може бути використано при перевірці оптимальності планів. Ми використаємо його при обговоренні питань економічної інтерпретації двоїстих змінних.

Дуже важлива так звана теорема рівноваги або, як її називають друга теорема двоїстості (критерій оптимальності допустимого базисного плану).

Твердження 1.7.4. Допустимий базисний план є розв’язком задачі (1.7.1) – (1.7.3) тоді і тільки тоді, коли існує вектор такий, що

, якщо

і