Содержание:

Теоретическая часть.

1. Подвижный репер поверхности……………………………………………………4

1.1. Метод подвижного репера поверхности…………………………………………4

2. Теория кривой................................................................................................................9

2.1.Регулярная кривая………………………………………………………………….9

2.2. Длина дуги. Естественная параметризация кривой……………………..............9

2.3. Касательная прямая и нормальная плоскость кривой………………………….11

2.4. Касательное отображение и касательное расслоение………………….............12

2.5. Соприкасающаяся плоскость…………………………………………….............12

2.6. Сопровождающий репер кривой………………………………………………...13

2.7. Кривизна кривой………………………………………………………………….14

2.8. Кручение кривой………………………………………………………………….14

2.9. Формулы Френе…………………………………………………………………..15

2.10. Уплощение кривой………………………………………………………...........16

2.11. Вычислительные формулы для кривизны и кручения………………………..17

2.12. Прямая, окружность, винтовая линия………………………………………….18

2.13. Задание кривой функциями кривизны и кручения……………………............19

2.14. Линии постоянных кривизн…………………………………………………….19

2.15. Строение кривой вблизи обыкновенной точки……………………………….19

3. Теория поверхности…………………………………………………………………21

3.1. Регулярная поверхность………………………………………………………….21

3.2. Линии на поверхности…………………………………………………………...22

3.3. Касательная плоскость и нормаль поверхности……………………………….22

3.4. Первая основная квадратичная форма поверхности…………………………...23

3.5. Метрика и поверхности……………………………………………………..........24

3.6. Кривизна линий на поверхности………………………………………………...26

3.7. Индикатриса кривизны…………………………………………………………..27

3.8. Классификация обыкновенных точек поверхности……………………………28

3.9. Главные кривизны на поверхности……………………………………………...29

3.10. Вычисление полной и средней кривизн поверхности………………………...29

Практическая часть

4. Кривая……………………………………………………………………………………31

4.1. Уравнение касательной…………………………………………………………..31

4.2. Уравнение нормальной плоскости………………………………………………31

4.3. Уравнение соприкасающейся плоскости……………………………………….32

4.4. Кривизна кривой…………………………………………………………….........32

4.5. Кручение кривой…………………………………………………………….........33

4.6. Изображение кривой……………………………………………………………..34

5. Поверхность……………………………………………………………………………..35

5.1. Уравнение плоскости…………………………………………………………….35

5.2. Уравнение нормали………………………………………………………………36

5.3. Первая квадратичная форма……………………………………………………..36

5.4. Вторая квадратичная форма……………………………………………………..37

5.5. Полная кривизна поверхности…………………………………………………..38

5.6. Средняя кривизна поверхности………………………………………………….38

5.7. Изображение поверхности……………………………………………………….39

Список литературы.

Теоретическая часть.

1. Подвижный репер поверхности.

1.1.Метод подвижного репера

Метод подвижного репера - дифференциально-геометрический метод локального исследования подмногообразий различных однородных пространств, исходным моментом котоpoгo является отнесение самого подмногообразия и всех его геометрических объектов к возможно более общему (подвижному) реперу. М. п. р. включает в себя последующий процесс канонизации репера - инвариантного присоединения к каждой точке подмногообразия единственного репера с целью получения дифференциальных инвариантов, характеризующих подмногообразие с точностью до преобразований вмещающего его однородного пространства.

В наиболее общей форме П. р. м. был предложен Г. Картаном, давшим разнообразные образцы его применений. Позднее метод получил широкое распространение и развитие. Аналитическую основу П. р. м. составляют инвариантные линейные дифференциальные формы группы Ли и их структурные уравнения, а также теория представлений групп Ли как групп преобразований. В современной геометрии основные положения П. р. м. потребовали уточнений и получили оформление в терминах теории расслоенных пространств.

Пусть есть n-мерное однородное пространство и G есть r-мерная группа Ли его преобразований (G действует слева). Пусть - представление, где - группа изотропии (стационарности) некоторой точки , ,- базис левоинвариантных векторных полей на G такой, что на Н составляют также базис левоинвариантных векторных полей подгруппы Ли H. Базису . Отвечает сопряженный базис левоинвариантных линейных дифференциальных форм на группе Ли G. Каноническая проекция , сопоставляющая точкам левые классы смежности группы G по подгруппе 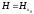, вносит в группу Ли G структуру главного H-расслоения с базой и структурной группой Н размерности r-п. При таком представлении G векторные поля составляют базис фундаментальных векторных полей расслоения 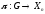, а векторные ноля натягивают некоторое трансверсальное к слоям расслоения n-распределение. В соответствии с этим линейные дифференциальные формы являются полубазовыми формами расслоения и образуют вполне интегрируемую подсистему форм в системе . Слои являются интегральными многообразиями максимальной размерности для системы уравнений Пфаффа q^k=0.

Системой реперов в классической дифференциальной геометрии (евклидовой, аффинной, проективной и т. д.) наз. множество фигур пространства , находящееся в биективном соответствии с множеством преобразований пространства (или, что то же самое, с множеством элементов фундаментальной группы G данного пространства), при этом любой репер R из данной системы можно получить из некоторого начального R₀ с помощью только одного преобразования:

.

Учитывая, что главная роль подвижного репера . По отношению к неподвижному R₀ состоит в том, чтобы определять произвольное преобразование однородного пространства , можно отождествить множество реперов с множеством элементов группового пространства G, приобретающих таким образом смысл абстрактных реперов, обслуживающих любое однородное пространство с данной фундаментальной группой G.

Пусть задано некоторое гладкое подмногообразие размерности т. Реперами нулевого порядка подмногообразия Мназ. элементы ограничения расслоения на М, как на новую базу. Это значит, что главное расслоение вложено в G и определяется в нем как полный прообраз . Так как левоинвариантные формы на группе Ли G подчиняются уравнениям Маурера – Картава:

(1)

где - структурные константы группы Ли, то ограничение форм 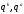на подрасслоение , т. е. формы 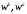будет подчиняться таким же уравнениям, но, сверх того, среди форм возникнут линейные зависимости

(2)

где - формы, оставшиеся вместе с линейно независимыми на главном расслоенном пространстве , а - функции, также определенные на расслоении реперов нулевого порядка Функции являются координатами касательной плоскости подмногообразия , зависящими от точки и репера

Касательные плоскости образуют сечение грассманова расслоения .

m-плоскостей, проходящих через точки подмногообразия . Расслоение является присоединенным к главному расслоению . Структура функций характеризуется уравнениями

(3)

явный вид которых можно получить внешним дифференцированием уравнений (2) с помощью (1) и последующим применением леммы Картана. Функций являются относительными координатами 1-струи сечения f по отношению к подвижному реперу точки . Геометрический объект образует также сечение соответствующего расслоенного пространства , присоединенного к главному расслоению . Аналогичным образом возникает сечение с координатами образующего его геометрического объекта, а также его последующие продолжения , которым соответствуют дифференциальные продолжения уравнений (3).

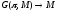До тех пор пока расслоение , которому принадлежит сечение , является однородным, возможна редукция главного расслоения реперов к некоторой подгруппе , определяемая по Картану с помощью некоторой фиксации относительных координат геометрического объекта , не зависящей от точки . Так определяется частичная канонизация репера. Реперы наз. полуканоническими реперами порядка q+1 данного подмногообразия 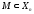. Если же следующее продолжение дает геометрические объекты, группа стационарности которых содержит лишь тождественное преобразование, то возможна фиксация лишь части координат геометрического объекта сечения , не зависящая от точки х, после чего оставшаяся часть координат L геометрического объекта зависит только от . Таким образом возникает сечение расслоения реперов нулевого порядка подмногообразия . Репер R=s(x).этого сечения наз. каноническим репером подмногообразия , или сопровождающим репером этого подмногообразия. Описанный выше процесс продолжения уравнений (3) и выбранный способ фиксации функций А приводит к уравнениям

(4)

связывающим линейные формы w^k, w^a на сечении s(M). Поле канонического репера строится не однозначно, а зависит от произвола фиксации относительных координат геометрич. объекта . Важно лишь то, что часть коэффициентов уравнения (4) имеет постоянные (при желании наиболее простые) числовые значения, тогда как другая часть их образует дифференциальные инварианты подмногообразия , определяющие его с точностью до преобразования в 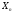. Канонические реперы сечения 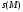являются аналогом классического примера - сопровождающего репера Френе кривой евклидова пространства, а уравнения (4) соответствуют уравнениям Френе кривой. На пути канонизации репера могут возникать осложнения, связанные с неоднородностью расслоений 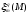и разнотипностью в этом смысле различных подмногообразий М в и даже их отдельных кусков. На этом и основывается классификация различных типов точек и различных классов подмногообразий в . Благодаря этим особенностям П. р. м. сыграл плодотворную роль в изучении подмногообразий в разнообразных однородных пространствах и, кроме того, указал путь к развитию современных методов исследования самых общих дифференциально-геометрических структур на гладких многообразиях.