
Безумовна багатопараметрична оптимізація
Пошук екстремуму за симплексом Метод Нелдера-Міда
інструкція до лабораторної роботи №4 з дисципліни "МОСК"
Мета роботи: вивчення та застосування на заданих прикладах критеріїв оптимізації одного із найбільш поширених методів безумовної багатопараметричної оптимізації – методу Нелдера-Міда.
1. Основні теоретичні відомості
Mетод Нелдера-Міда – це евристичний метод прямого пошуку, побудований на проведенні експериментів та визначенні (обчисленні) тільки значень критерію.
Обмеження на критерій оптимальності – унімодальність.
Метод застосовується при пошуку мінімуму критерію на реальних об’єктах та їх моделях в задачах багатопараметричної оптимізації при відсутності обмежень на параметри оптимізації.
Означення
Симплекс – це багатогранник (зразок) в просторі параметрів оптимізації з найменшою кількістю точок – вершин зразка. Для випадку двопараметричної задачі оптимізації, коли простір параметрів оптимізації є площиною, таким зразком є трикутник.
Регулярний симплекс в N-вимірному просторі параметрів оптимізації – це багатогранник, утворений з N+1 рівновіддалених одна від одної точками – вершинами багатогранника.
На площині (N = 2) регулярний симплекс – це правильний трикутник (рисунок 1, а). В тривимірному просторі параметрів оптимізації (N = 3) – тетраедр (рисунок 1, б), для N > 3 – гіпертетраедр.
На рисунках 1 а,б зображені:
1 – регулярний симплекс;
2 – деформований (скорочений) симплекс;
3 – деформований (видовжений) симплекс.


а б
Рисунок 1. Приклади регулярних та деформованих симплексів у двовимірному (а) та тривимірному (б) просторі параметрів оптимізації Х1, Х2, Х3
1.1 Послідовність пошуку мінімуму за симплексом:
-
Побудова початкового регулярного симплексу при заданій початковій точці х(0) та заданій довжині ребра регулярного симплексу α.
-
Проведення експериментів по визначенню значень критерію у всіх точках (вершинах) регулярного симплексу та вибір “найгіршої” та двох “кращих” точок симплексу.
“Найкраща” точка симплексу – це одна із вершин симплексу, в якій значення критерію є найменшим.
“Найгірша” точка симплексу – це одна із вершин симплексу, в якій значення критерію є найбільшим;
-
Побудова нового (відбитого) симплексу.
-
Проведення експерименту по визначенню критерію у новій точці відбитого симплексу та порівняння його значення з найгіршою та двома кращими точками початкового симплексу.
-
Прийняття рішення про видовження/скорочення відбитого симплексу (в залежності від результатів порівняння в п.4) та обчислення координат нової відбитої точки.
-
Перевірка умов зупинки пошуку та повернення до п.3 у випадку їх невиконання.
1.2 Побудова початкового регулярного симплексу
Для побудови початкового регулярного симплекса потрібно, щоб були задані х(0) – початкова точка і α – довжина ребра.
В методі Нелдера-Міда для початкового симплексу α = 1, а координати вершин регулярного симплексу обчислюють за формулою:

де: і – номер вершини регулярного симплекса (на площині і=1,2,3);
j – номер координати вершини в N-вимірному просторі (на площині j=1,2);

N – число параметрів оптимізації.
Приклад побудови початкового регулярного симплексу для N=2
 ;
;

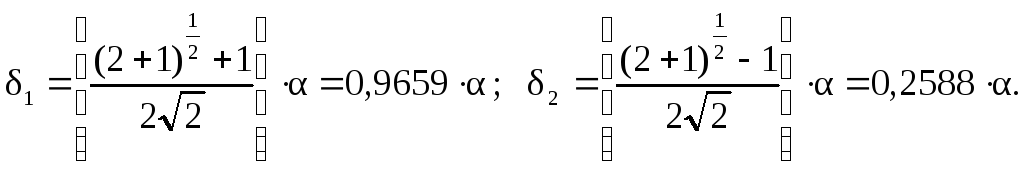
Приклад побудови початкового регулярного симплексу для N=3
 ,
,





а б
Рисунок 2. Орієнтація регулярних початкових симплексів за методом Нелдера-Міда:
а – для N=2; б – для N=3
1.3 Проведення експериментів по визначенню значень критерію в точках (вершинах) початкового симплексу та вибір двох найкращих точок симплексу
а) Визначають значення критерію у вершинах симплексу f(1), f(2), f(3), ..., f(N), f(N+1), де f(і) – значення критерію в і – тій вершині симплексу.
б) Із N+1 вершин симплексу вибирають “найгіршу” точку симплексу (k – вершину з найбільшим значенням критерію f(k)) і позначають її як х(h) (присвоюють х(h) = х(k), f(h)= f(k)).
в) Із N+1 вершин симплексу вибирають дві вершини, в яких значення критерію є найменшими (f(g) та f(l), f(g) f(l)) і позначають їх як х(g) та х(l) відповідно.
