
- •Вибірка з генеральної сукупності. Розподіл вибірки. Вибіркові характеристики. Загальні поняття математичної статистики.
- •Надійний інтервал для математичного сподівання ознаки γ нормальним законом розподілу і відомим середньоквадратичним відхиленням.
- •Приклад.
- •Інтервал надійності для оцінки математичного сподівання з нормальним розподілом випадкової величини та не відомим значенням σ.
- •Довірчий інтервал, інтервал надійності оцінки середньоквадратичного відхилення з нормальним законом розподілу.
- •В) .Поняття про умовні варіанти. Метод добутків для знаходження вибіркових середніх і дисперсії.
- •А дисперсія вибірки
- •Складаємо наступну розрахункову таблицю
- •Отже вибрана нами точка-
Складаємо наступну розрахункову таблицю
|
Xi |
ni |
Ui |
niUi
|
niU²i |
|
5 |
18 |
- 2 |
- 36 |
72 |
|
11 |
20 |
- 1 |
- 20 |
20 |
|
17 |
25 |
0 |
0 |
0 |
|
23
|
37 |
1 |
37 |
37 |
|
100 |
- 19 |
129 |
Отже вибрана нами точка-
![]() = 17 ,
= 17 ,
![]() =
1/100 ( - 19) = -0,19
=
1/100 ( - 19) = -0,19
![]() = 17 + ( - 0.19)6 = 15,86
= 17 + ( - 0.19)6 = 15,86
S² = 6² ((1/100)129 – ( - 0,19)²) = 45,14
Відмітимо що при обчислені вибіркової дисперсії для зменшення помилки, викликаної групуванням ( особливо при малому числі інтервалів ) роблять поправку Шеппарда і обчислюють дисперсію за формулою
![]()
Отже,групування спрощує обчислення, але при цьому, зрозуміло, втрачається деяка інформація, про що свідчить наявність поправки Шепарда.
Г)Багатовимірні випадкові величини.
Нехай є впорядкована система n
випадкових величин
![]() .Називатимемо її n-
вимірною випадковою величиною і
позначатимемо так:
.Називатимемо її n-
вимірною випадковою величиною і
позначатимемо так:
![]()
Тоді ![]() – це i-та
випадкова величина. Упорядковану
систему з n
випадкових величин можна розглядати і
як випадкову точку з координатами
– це i-та
випадкова величина. Упорядковану
систему з n
випадкових величин можна розглядати і
як випадкову точку з координатами
![]() у n-
вимірному евклідовому просторі
у n-
вимірному евклідовому просторі ![]() .
.
Щоб задати випадковий вектор,потрібно вказати всі ті значення ,яких він може набувати,і ймовірності,з якими ці значення набуваються.Універсальним способом задання випадкового вектора є задання його інтегральної функції розподілу,яка визначається рівністю:
![]() ,
,
![]()
Це ймовірність того,що
![]()
Зупинимося детальніше на двовимірному
випадку.При цьому нехай ![]() ,а
,а
![]() .Властивості інтегральної функції
розподілу двовимірної випадкової
величини аналогічні властивостям
функції розподілу випадкової
величини.Перерахуємо їх.
.Властивості інтегральної функції
розподілу двовимірної випадкової
величини аналогічні властивостям
функції розподілу випадкової
величини.Перерахуємо їх.
-

-
Fє неспадна функція по кожній із змінних.
-
 ,
, -
,
 ,
,
![]()
![]()
Двовимірну випадкову величину називають
дискретною ,якщо множина значень,яких
вона може набути,є скінченною або
зліченою.Для задання такої величини
досить задати її можливі значення ![]() і ймовірності кожного з них :
і ймовірності кожного з них :
![]() .Закон розподілу такої величини може
бути заданий у вигляді таблиці з двома
входами
.Закон розподілу такої величини може
бути заданий у вигляді таблиці з двома
входами
|
|
|
|
…….. |
|
………… |
|
|
|
|
|
…….. |
|
……….... |
|
|
|
|
|
…….. |
|
………… |
|
|
……. |
……… |
…….. |
…….. |
…….. |
………… |
……… |
|
|
|
|
…….. |
|
…………. |
|
|
……… |
………… |
…….. |
…….. |
………… |
………… |
………… |
|
|
|
|
…….. |
|
………… |
1 |
Тут використано позначення:
![]() ,
,
![]()
З аксіоми адитивності випливає,що
![]()
Аналогічно
![]()
Таким чином,ймовірності ![]() задають розподіл випадкової величини
задають розподіл випадкової величини
![]() розподіл випадкової
величини
розподіл випадкової
величини ![]() .При цьому:
.При цьому:
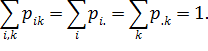
Функція розподілу випадкового вектора
![]() визначається рівністю
визначається рівністю

Де сумування поширюється на всі
![]() ,для яких
,для яких ![]() а k набуває
усіх значень, для яких
а k набуває
усіх значень, для яких
![]() .
.
Приклад 1.Якість продукції
характеризується двома випадковими
параметрами ![]() і
і ![]() .Закон розподілу двовимірної випадкової
величини
.Закон розподілу двовимірної випадкової
величини
![]() задано
таблицею
задано
таблицею
![]() :
:
|
|
5 |
6 |
7 |
|
|
0 |
0,2 |
0 |
0 |
0,2 |
|
0,1 |
0,1 |
0,15 |
0 |
0,25 |
|
0,2 |
0,05 |
0,15 |
0,1 |
0,3 |
|
0,3 |
0,05 |
0,1 |
0,1 |
0,25 |
|
|
0,4 |
0,4 |
0,2 |
1 |
Знайти закони розподілу випадкових
величин
![]() i
i
![]() .
.
Доповнимо таблицю рядком і стовпчиком
зі знаком
![]() ,провівши сумування величин
,провівши сумування величин
![]() відповідно по рядках і стовпчиках.Тоді
очевидно,що закони розподілу випадкових
величин
відповідно по рядках і стовпчиках.Тоді
очевидно,що закони розподілу випадкових
величин ![]() i
i
![]() мають вигляд:
мають вигляд:
|
|
5 |
6 |
7 |
|
||||||||
|
p |
0,4 |
0,4 |
0,2 |
|
||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
|
|
0 |
0,1 |
0,2 |
0,3 |
|
p |
0,2 |
0,25 |
0,3 |
0,25 |
Двовимірну випадкову величину
![]() називають неперервною,якщо існує така
функція p ,що функція розподілу
F даної випадкової величини може
бути подана у вигляді
називають неперервною,якщо існує така
функція p ,що функція розподілу
F даної випадкової величини може
бути подана у вигляді

Функцію називають щільністю розподілу
випадкового вектора
![]() .При цьому:
.При цьому:
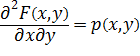
У точках неперервності функції p.
Щільність розподілу має такі властивості:
-
 ;
; -
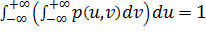 .
.
Знаючи щільність розподілу
p двовимірної величини
![]() ,легко знайти щільності розподілу для
її компонент
,легко знайти щільності розподілу для
її компонент ![]() та
та ![]() .Справді,
.Справді,

Звідки

Аналогічно

І

Нехай задана дискретна двовимірна
випадкова величина
![]() .Розглянемо функцію розподілу випадкової
величини
.Розглянемо функцію розподілу випадкової
величини
![]() за умови , що
за умови , що ![]() набула значення
набула значення ![]() ,
,
![]() .Цю функцію позначають
.Цю функцію позначають
![]() .Імовірність того,що
.Імовірність того,що
![]() набуває значення
набуває значення ![]() ,коли
,коли ![]() набуло значення
набуло значення
![]() ,дорівнює
,дорівнює

Аналогічно

У випадку неперервного розподілу вектора
![]() з’являються умовні щільності роз
поділу
з’являються умовні щільності роз
поділу
![]() ,коли
,коли ![]() ,
і
,
і
![]() , коли
, коли ![]() .Можна довести,що
.Можна довести,що
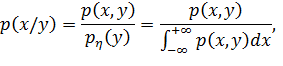

Випадкова величина
![]() називається незалежною від
випадкової величини
називається незалежною від
випадкової величини
![]() ,якщо розподіл
,якщо розподіл
![]() не залежить від того,якого значення
набула випадкова величина
не залежить від того,якого значення
набула випадкова величина
![]() .Аналогічно
визначається незалежність
.Аналогічно
визначається незалежність
![]() від
від
![]() .Якщо величини
.Якщо величини
![]() і
і
![]() незалежні,то
незалежні,то ![]() (дискретний розподіл) і
(дискретний розподіл) і ![]() (неперервний розподіл).
(неперервний розподіл).
Приклад 2.Нехай щільність розподілу двовимірної випадкової величини

Знайти функції розподілу випадкового
вектора
![]() ,випадкових величин
,випадкових величин
![]() і
і
![]() ,умовні щільності розподілу.
,умовні щільності розподілу.
![]() Спочатку
доведемо коректність означення
випадкового вектора
Спочатку
доведемо коректність означення
випадкового вектора
![]() :
:
-
 ,що очевидно.
,що очевидно. -

Знайдемо функцію розподілу даного
випадкового вектора
![]() :
:

Для всіх інших точок (x,y)
F(x,y)=0
.Очевидно,що ![]() при x<0,
бо
при x<0,
бо
![]() не набуває від’ємних значень ;якщо
x>0 ,то:
не набуває від’ємних значень ;якщо
x>0 ,то:

Далі

![]() .
.
Аналогічно ![]() і
і
![]()
![]() .
.
