4.2. Решение типового варианта контрольной работы n 2

Задача 2.1. Найти , если , , .

Решение. а). Для имеем

.

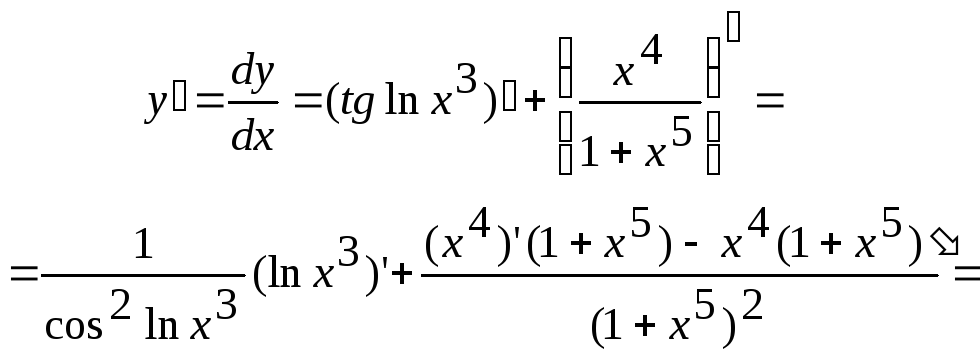
б). Для .

.

в). Для .

.

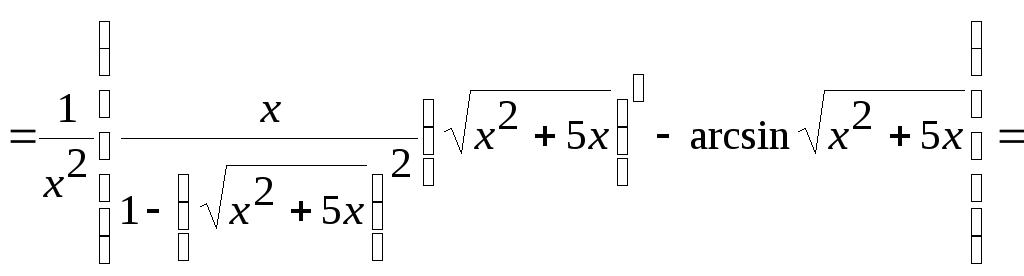
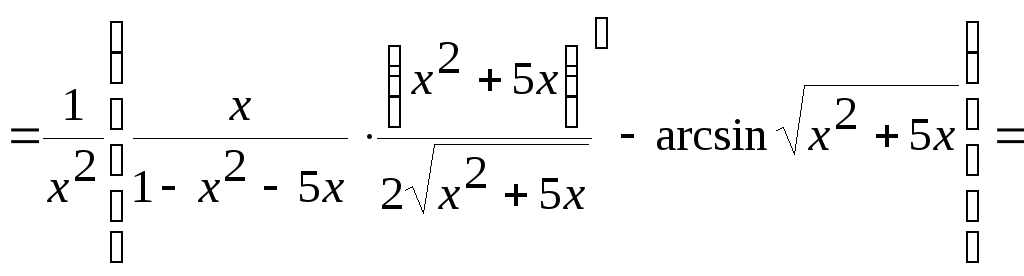
Задача 2.2. Найти , если

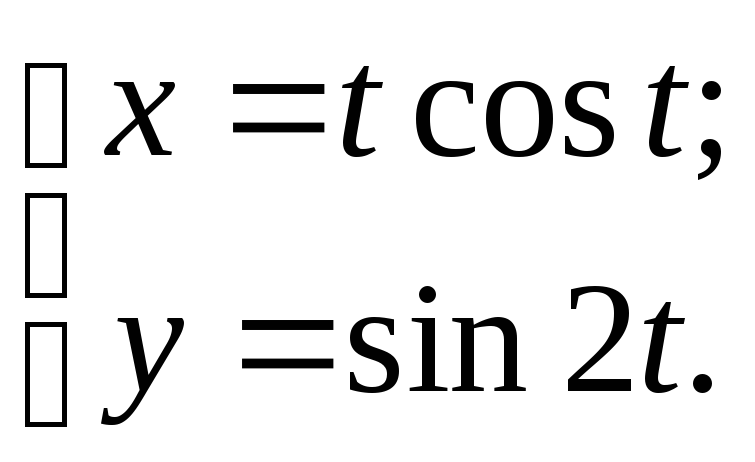
Решение

а).

б). Дифференцируя уравнение для , имеем

,

откуда

.

Дифференцирование последнего соотношения дает

.

Внося выражение для , находим

.

в). Первая производная заданной параметрически функции вычисляется по формуле

.

Здесь

,

откуда

.

Вторую производную вычислим по формуле

.

Задача 2.3. Вычислить предел, пользуясь правилом Лопиталя:

.

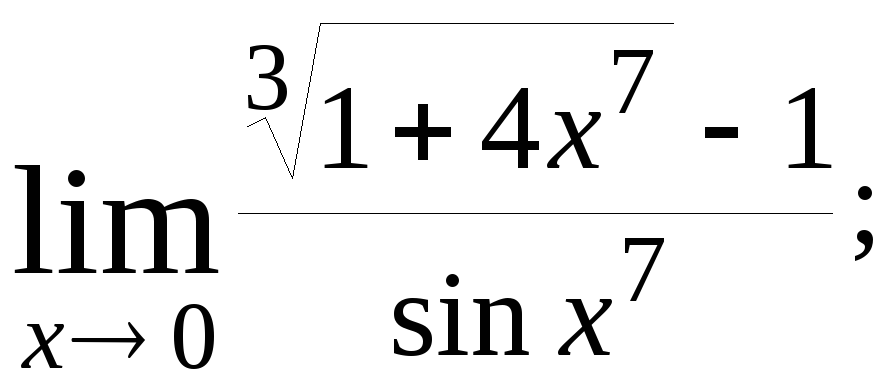
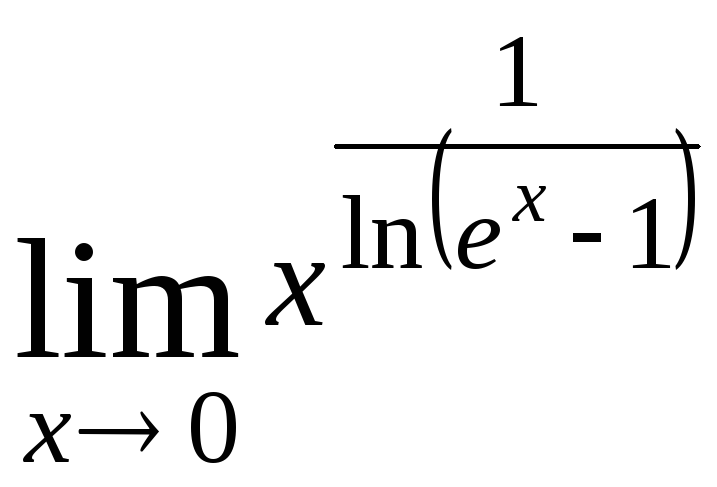Решение. а). Искомый предел является неопределённостью типа

По правилу Лопиталя

.

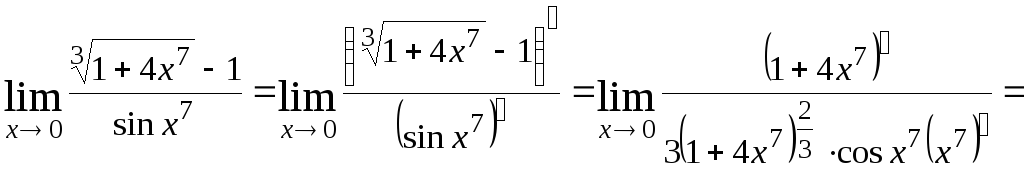
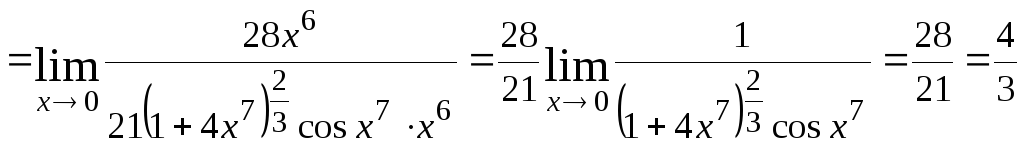б). Предел является неопределённостью вида поэтому вначале его надо преобразовать к виду или :

.

К последнему (типа ) можно применять правило Лопиталя:

.

Полученный предел вновь является неопределенностью поэтому повторное применение правила дает

.

в). Предел является неопределенностью вида к которой удобно применять следующий прием. Обозначим

.

Тогда

. (1)

Вычислим вспомогательный предел

.

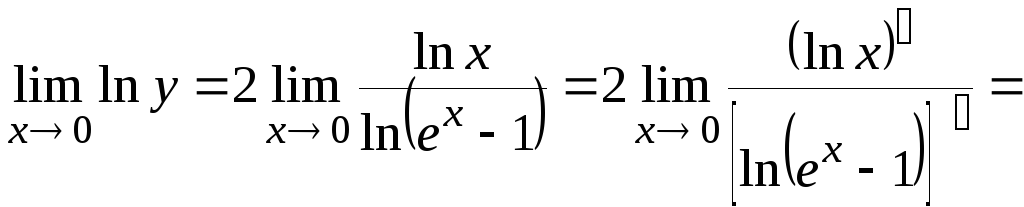
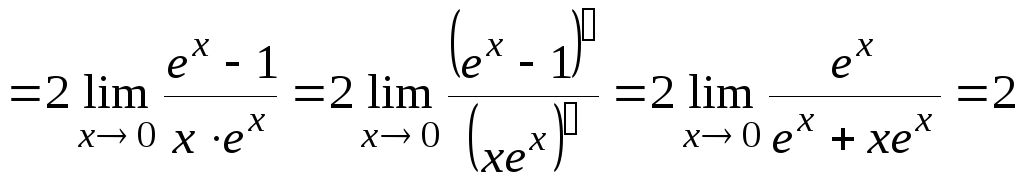Искомый предел согласно (1) равен

.

Задача 2.4. Исследовать функцию и построить ее график.

Решение. Областью определения является вся действительная ось . Для отыскания участков монотонности находим

.

Тогда при (интервал возрастания), при (интервал убывания). Точка является стационарной, поскольку При переходе через производная меняет знак с плюса на минус, поэтому при функция имеет локальный максимум.

Для отыскания участков выпуклости используется вторая производная

.

При или будет и функция вогнута; при и функция выпукла.

Вертикальных асимптот функция не имеет. Для отыскания наклонных асимптот вычислим

.

Поэтому при функция имеет асимптоту

Результаты исследования с учетом четности функции показаны на графике

Y

2

1

X

О

4.3. Решение типового варианта контрольной работы n 3

Задача 3.1. Найти градиент и уравнения касательной плоскости и нормали к заданной поверхности в точке .

.

Решение. Обозначим

Тогда

;

.

Величина градиента

.

Уравнение касательной плоскости, имеющей нормальный вектор (7,-4,-19) и проходящей через , запишется

,

или

.

Нормальная прямая имеет направляющий вектор (7,-4,-19) и проходит через , поэтому ее уравнения

.

Задача 3.2. Найти наибольшее и наименьшее значения функции в области D, ограниченной заданными линиями:

Решение. Область D показана на рисунке (треугольник OAB).

y

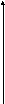
B(0,6)

D

1 С

0 2 A(3,0) x

Cтационарные точки являются решениями системы уравнений

,

откуда находим точку , принадлежащую, как видно из рисунка, области . В этой точке . (2)

Исследуем функцию на границе области D.

Отрезок ОА. Здесь и Стационарные точки определяются из уравнения откуда В этой точке

. (3)

На концах отрезка

, . (4)

Отрезок АВ. Здесь и Из уравнения находим и

. (5)

При имеем

. (6)

Отрезок ОВ. Здесь Поскольку при функция не имеет стационарных точек. Значения ее при были вычислены в (4), (6).

Из результатов (2)-(6) заключаем, что

причем наибольшее значение достигается в точке А(3,0), наименьшее - в точке С(2,1).

Задача 3.3. Найти полный дифференциал функции

Решение. Частные производные равны

Поэтому

.

Задача 3.4. Найти частные производные второго порядка функции

Решение. Сначала находим частные производные первого порядка:

Затем, дифференцируя найденные частные производные, получим частные

производные второго порядка данной функции:

Задача 3.5. Вычислить значение производной сложной функции

где

,

при с точностью до двух знаков после запятой.

Решение. Так как сложная функция зависит от одной переменной через промежуточные переменные и, которые в свою очередь зависят от одной переменной то вычисляем полную производную этой функции по формуле

.

.

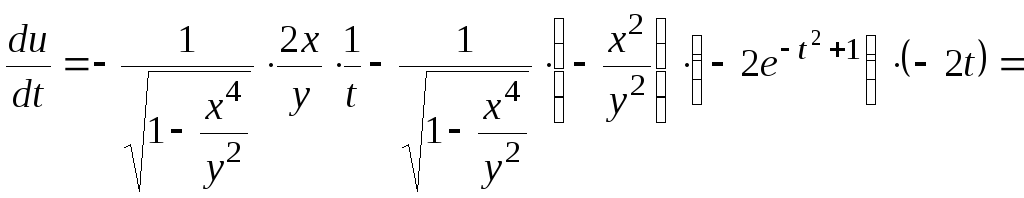
Вычислим и при :

.

Подставим значения в выражение производной. Получим

.