
- •III.1. Регулярная поверхность.
- •III.2. Линии на поверхности.
- •III.3. Касательная плоскость и нормаль поверхности.
- •III.4. Первая основная квадратичная форма поверхности.
- •III.5. Метрика на поверхности.
- •III.6. Кривизна линий на поверхности.
- •III.7. Индикатриса кривизны.
- •III.8. Классфикация обыкно венных точек поверхности.
- •III.9. Главные кривизны на поверхности.
- •III.10. Вычисление полной и средней кривизн поверхности.
- •III.11. Плоскость, сфера, псевдосфера.
III.1. Регулярная поверхность.
На
евклидовой плоскости
 выбрана некоторая область
выбрана некоторая область
 ,
гомеоморфная прямоугольнику. Можно
считать, что
,
гомеоморфная прямоугольнику. Можно
считать, что
 прямоугольник. Он состоит из точек
прямоугольник. Он состоит из точек
 ,
,
 ,
т.е.
,
т.е.
 ,
,
 и
и
 , область
, область
 может совпадать с
может совпадать с
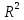 .
Плоскость
.
Плоскость
 есть пара
есть пара
 ,
где
,
где
 евклидова метрика на
евклидова метрика на
 .
Задано отображение
.
Задано отображение

плоской
области
 в евклидово пространство
в евклидово пространство
 ,
в котором точке
,
в котором точке
 из
из
 соответствует точка
соответствует точка
 из
из
 ,
в
,
в
 .
Отображение
.
Отображение
 является гомеоморфным - взаимно
однозначным и взаимно непрерывным. В
является гомеоморфным - взаимно
однозначным и взаимно непрерывным. В
 выбран ортонормированный репер
выбран ортонормированный репер
 . При изменении точки
. При изменении точки
 в области
в области
 изменяется точка
изменяется точка
 в пространстве
в пространстве
 .
Координаты
.
Координаты
 ,
,
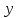 ,
,
 точки
точки
 являются функциями координат точки
являются функциями координат точки
 :
:
 ,
,
 ,
,
 ,
,
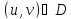 .
.
Эти
функции непрерывны, ввиду того, что
отображение
 гомеоморфно. Таким образом, имеется
векторная функция двух параметров
гомеоморфно. Таким образом, имеется
векторная функция двух параметров
 ,
,
 .
.
Отображение
 и образ области
и образ области
 в отображении
в отображении
 называется поверхностью.
Поверхность есть множество точек
называется поверхностью.
Поверхность есть множество точек
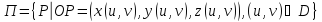 .
.
Задается поверхность векторной функцией

Поверхность
 составляют концы векторов
составляют концы векторов
 ,
поэтому поверхность
,
поэтому поверхность
 называется годографом функции
называется годографом функции
 .
.
Наложим
на функцию
 условия:
условия:
-
 есть
функция класса
есть
функция класса
 ,
т.е. существуют непрерывные частные
производные этой функции до третьего
порядка включительно;
,
т.е. существуют непрерывные частные
производные этой функции до третьего
порядка включительно; -
Векторы
 ,
,
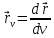 неколлинеарны в точках области
неколлинеарны в точках области
 .
Неколлинеарность, векторов означает,
в частности, что они ненулевые, а также
означает, что ранг следующей матрицы
равен 2:
.
Неколлинеарность, векторов означает,
в частности, что они ненулевые, а также
означает, что ранг следующей матрицы
равен 2:
 .
.
Поверхность,
заданная векторной функцией с указанными
условиями, называется регулярной класса
 .
Область
.
Область
 задания поверхности можно считать
окрестностью всякой ее внутренней точки
задания поверхности можно считать
окрестностью всякой ее внутренней точки
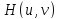 ,
,
 ,
,
 .
Всякая точка регулярной поверхности
называется обыкновенной.
Мы изучаем поверхности в окрестности
обыкновенной точки.
.
Всякая точка регулярной поверхности
называется обыкновенной.
Мы изучаем поверхности в окрестности
обыкновенной точки.
III.2. Линии на поверхности.
Фиксируя
на поверхности
 один из параметров, получаем на поверхности
регулярную кривую, см. п. II.1.
Имеем следующие линии:
один из параметров, получаем на поверхности
регулярную кривую, см. п. II.1.
Имеем следующие линии:
-
 -линии
поверхности, это линии
-линии
поверхности, это линии
 ,
,
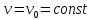 ;
;
-
 -линии
-линии
 ,
,
 .
.
Всякие
две -линии и всякие две
 -линии
поверхности не пересекаются. Чрез каждую
точку поверхности проходит единственная
-линия и единственная
-линии
поверхности не пересекаются. Чрез каждую
точку поверхности проходит единственная
-линия и единственная
 -линия.
Таким образом, на поверхности имеется
криволинейная координатная сеть. С
каждой точкой
-линия.
Таким образом, на поверхности имеется
криволинейная координатная сеть. С
каждой точкой
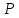 поверхности связан репер
поверхности связан репер
 ;
производные
;
производные
 ,
,
 вычислены в точке
вычислены в точке
 ,
,
 .
.
Если
в области
 заданы функции
заданы функции
 ,
,
 ,
то на поверхности
,
то на поверхности
 определяется линия
определяется линия
 ,
,

Это произвольная линия на поверхности.
III.3. Касательная плоскость и нормаль поверхности.
Пусть
 точка регулярной поверхности
точка регулярной поверхности
 . В этой точке имеем неколлинеарные
векторы
. В этой точке имеем неколлинеарные
векторы
 ,
,
 .
Для любой линии
.
Для любой линии
 выполняется
выполняется
 ,
,
т.е.
вектор касательной
 всякой линии поверхности
всякой линии поверхности
 ,
проходящей через точку
,
проходящей через точку
 ,
является линейной комбинацией векторов
,
является линейной комбинацией векторов
 ,
,
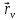 - векторов касательных -линии и
- векторов касательных -линии и
 -линии;
вектор
-линии;
вектор
 принадлежит оболочке
принадлежит оболочке
 . Касательная прямая
. Касательная прямая
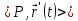 всякой кривой
всякой кривой
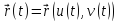 поверхности
поверхности
 лежит в плоскости
лежит в плоскости
 .
Касательные всех линий поверхности
.
Касательные всех линий поверхности
 ,
проходящих через точку
,
проходящих через точку
 ,
образуют плоскость. Получена следующая
,
образуют плоскость. Получена следующая
III.3.1.
ТЕОРЕМА.
Регулярная
поверхность
 в каждой своей точке
в каждой своей точке
 обладает касательной плоскостью <
обладает касательной плоскостью < .
#
.
#
Пусть
 и производные
и производные
 ,
,
 вычислены в точке
вычислены в точке
 .
Тогда уравнение касательной плоскости
таково
.
Тогда уравнение касательной плоскости
таково
 .
.
Прямая
 называется нормалью поверхности
называется нормалью поверхности
 в точке
в точке
 .
Ее уравнения:
.
Ее уравнения:
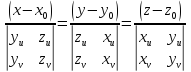 .
.
