1. Теоретические аспекты информационных технологий.

Данный раздел предназначен для определения понятий и терминов, которые понадобятся для изложения последующего материала. Читатели, знакомые с основами теории сигналов и информации, могут его опустить; те же, кто пожелают углубить его изучение, могут обратиться к приведенному библиографическому списку.

1. Теория сигналов и спектральный анализ

Обратимся вначале к общей структуре системы передачи информации, изображенной на рис. 1.1.

З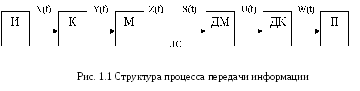десь обозначено: И - источник сообщений (информации); К - кодер (кодирующее устройство); М - модулятор; ЛС - линия связи; ДМ- демодулятор; ДК - декодер; П - приемник сообщений. Это наиболее общая схема, которой можно описать большинство процедур передачи информации. Например, при речевом обращении роль источника выполняет мозг человека, кодер - его словообразующая часть, модулятор - ротоносовая полость, демодулятор - ухо собеседника, декодер и приемник - его головной мозг.

При любой процедуре передачи сообщений есть общее свойства. Источник вырабатывает какую-то изменяющуюся во времени функцию, которая преобразуется в изменение одного из параметров среды передачи (акустический канал - звуковые волны, проводной - электрические параметры, радиоканал - электромагнитное излучение). Эта функция и называется сигналом. Поскольку при этом передается информация, часто определяют сигнал как материальный носитель информации. Сигнал - всегда функция времени, причем, исходя из природы передачи информации, это случайная функция. Будем обозначать ее U(t).

Для описания сигналов удобнее вначале рассмотреть некоторые частные случаи по общефилософской концепции "от простого - к сложному". В этом случае пытаются перейти от термина "сигнал" к термину "колебание", понимая под этим произвольную функцию времени. В дальнейшем мы сохраним одинаковое обозначение для сигналов и колебаний.

Существуют естественные ограничения на любой сигнал, вытекающие из физической природы источников сообщений.

1.Реальный сигнал ограничен по амплитуде и скорости нарастания:

;	(1.1)
.	(1.2)

Здесь символ  обозначает квантор общности и означает, что выражения (1.1) и (1.2) справедливы для любых значений времени t.

2. Мощность реального сигнала, мгновенная p(t) или интервальная P_Т(t), а также его энергия W ограничены по величине:

р(t) <  |t;	(1.3)
PT(t) <  |t;	(1.4)
.	(1.5)

3.Сигнал ограничен по времени:

U(-)=U()=0.

(1.6)

Эти ограничения вполне очевидны для любого искусственного источника информации. Мгновенную и интервальную мощности можно определить следующим образом:

p(t)=U2 (t);	(1.7)
.	(1.8)

Один из классов колебаний - периодические, повторяющие свои значения с интервалами, кратными целому числу периодов:

U(t)=U(t  mT) |t.

(1.9)

Строго говоря, это - математическая абстракция, поскольку нарушаются ограничения 2 и 3. Тем не менее, для первичного анализа бывает полезно рассматривать сигналы в виде периодических функций. Кроме того, некоторые природные процессы носят периодический характер (суточные колебания температуры и освещённости, изменения потребления электроэнергии, сезонные изменения и т.д.). Для земного наблюдателя они не ограничены во времени (то есть, время их действия намного выше времени наблюдения).

При описании сигналов широко используется метод аналогий, то есть, сравнения исследуемых сигналов с известными, а также сравнения различных сигналов между собой с помощью типичных колебаний. В этом смысле используются разложение колебаний в ряды по системам функций. Математически эта задача формулируется следующим образом: произвольную функцию времени U(t) нужно представить суммой некоторых базисных функций _i(t) в виде:

,

(1.10)

где a_k - постоянные величины (коэффициенты разложения).

Ряд (1.10) ограничен сверху значением N <  из чисто практических соображений. Критерием для такого ограничения чаще всего является принцип достаточности мощности: учитываемое число N членов разложения содержит достаточно большую долю полезной мощности сигнала U(t):

,

(1.11)

где m - доверительный коэффициент, близкий к единице (m<1).

Последний член в равенстве (1.11) показывает на способ вычисления мощности исследуемого сигнала; здесь Т - время существования сигнала или период повторения.

Сформулируем требования к функциям разложения _i(t).

1. Базисные функции должны сравнительно просто описываться или генерироваться. Если они вычисляются, наиболее простым может быть вычисление через номер функции k или по рекурсивной процедуре:

k+1(t) = z[k(t)].

(1.12)

2. Желательно подобрать такие функции, чтобы ряд (1.10) как можно быстрее сходился (то есть, количество N в выражениях (1.10) и (1.11) было как можно меньшим).

Общая постановка задачи расположения в ряд (1.10) формулируется следующим образом [5]: по заданной базисной системе функций _k(t) найти значения a_k, обеспечивающие минимальную погрешность разложения:

.

(1.13)

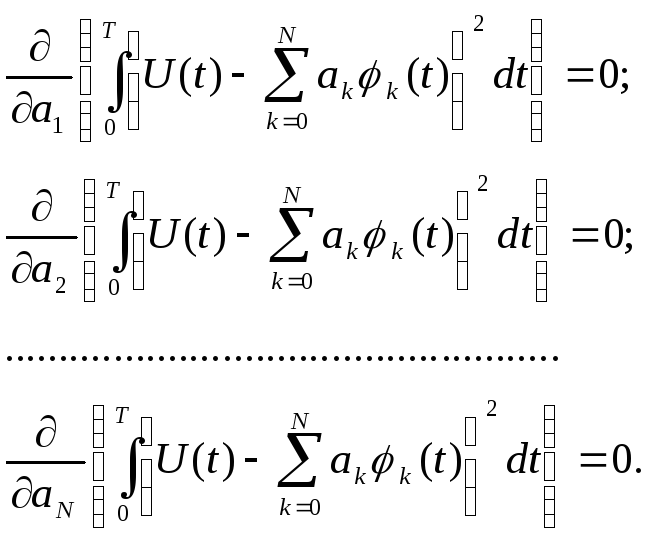
Очевидно, для обеспечения минимума выражения (1.13) необходимо частные производные по a_k приравнять к 0 и решить полученную систему уравнений, которая примет вид:

(1.14)

В общем случае система уравнений (1.14) решается достаточно сложно, поэтому ограничимся частным классом функций разложения - ортогональными функциями. Они определяются следующим соотношением:

.

(1.15)

В частности, если М=1, функции называются ортонормальными. При таком допущении решение уравнений (1.14) получается достаточно простым:

.

(1.16)

В более общем случае функции могут быть ортогональными с весом:

,

(1.17)

где r(t) - весовая функция, приводящая базисные функции к ортогональности.

Тогда

.

(1.18)

Наиболее часто в качестве функций разложения используются тригонометрические функции. Поскольку в соответствии с (1.15) , для нормирования необходимо коэффициенты разложения домножать на . Ряд (1.10) можно представить в двух равнозначных формах [12]:

;	(1.19)
.	(1.20)

Эти формулы связаны между собой соотношениями:

; k = arctg(bk/ak ).

(1.21)

В свою очередь, коэффициенты разложения вычисляются по формулам:

	(1.22)
.	(1.23)

Выражения (1.20) и (1.23) образуют пару преобразований для ряда Фурье, соответственно прямое и обратное преобразования.

Совокупность амплитуд и фаз ряда Фурье формы (1.20) называется спектром колебания U(t). Наибольший практический интерес представляет спектр амплитуд, определяющий мощность колебания:

.

(1.24)

Спектр фаз определяет форму колебания, что представляет не такой большой интерес.

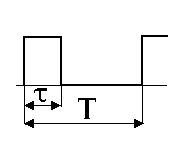
Приведем пример. Получим спектр периодической последовательности прямоугольных импульсов длительностью  (см. рис.1.2).

Для упрощения расчетов примем начало координат посредине импульса; тогда выражение примет вид:

(1.25)

Согласно (1.23)

.

(1.26)

Упростим выражение, подставив  = 2/T и применив формулу Эйлера:

.

(1.27)

Отношение T/ называется скважностью Q. Тогда (1.27) преобразуется к виду:

.

(1.28)

П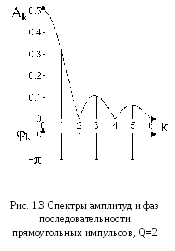римем теперь  =T/2, то есть Q=2. Из (1.28) следует, что гармонические составляющие с четными к обращаются в 0, а нечетные имеют амплитуды |A| =2E/K. Общий вид спектра приведен на спектральной диаграмме, показанной на рис.1.3.

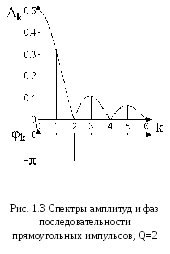
На диаграмме по горизонтали откладываются номера гармоник, по вертикали - их амплитуды. Штриховой линией на диаграмме показана так называемая огибающая спектра. Она образуется при подстановке в (1.28) непрерывно изменяющегося аргумента вместо к.

Н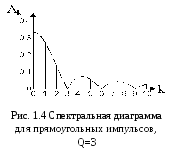а рис.1.4. приведена диаграмма спектра амплитуд при уменьшенной длительности импульсов (Q=3). Видно, что равны 0 гармоники с номерами, кратными 3, а все спектральные линии уменьшают амплитуду. Отсюда можно сделать вывод, что сокращение длительности колебания приводит к расширению его спектра.

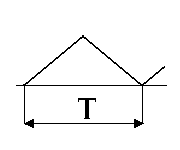
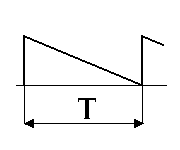
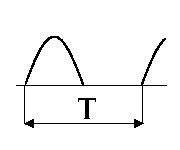
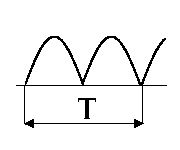
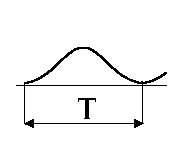
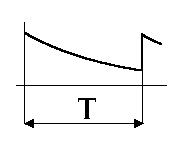
В табл. 1.1. приведены спектры наиболее широко распространенных периодических колебаний.

Таблица 1.1.

Спектры типовых сигналов

№	Вид колебания	График U(t)	Спектр амплитуд Аk	Аналитическое выражение
1	Прямоуголь-ные импульсы
2	Треугольное			U(t) = 1-2t/T
3	Пилообразное			U(t) = t
4	Однополупе-риодное выпрямление			cos t
5	Двухполупе-риодное впрямление		, m - четное	|sin t|
6	Косинус -квадратное			cos2t
7	Колокольное
8	Экспоненци-альное

Кроме широко распространенных в цифровой технике прямоугольных импульсов, в системах цифровой связи используются импульсы вида косинус-квадрат с наиболее узкой полосой. Одно из наиболее узкополосных колебаний - треугольное. Его сравнительно легко сформировать интегрированием прямоугольных импульсов, поэтому такого вида колебания можно использовать в узкополосных каналах. Колебания вида 7 и 8 хорошо иллюстрируют зависимость ширины спектра от скорости изменения: чем выше скорость (чем больше ), тем шире спектр (тем меньше убывают амплитуды A_к при увеличении к). Здесь Ф(z) - функция Лапласа [11].

Все непериодические колебания называются импульсами, независимо от их формы. Применительно к импульсам пара преобразований Фурье (1.20), (1.23) видоизменяется, поскольку период такого колебания условно считается стремящимся к бесконечности. В результате вместо рассмотренных нами спектров в виде совокупности спектральных линий образуются сплошные кривые, называемые спектральными характеристиками, а ряд Фурье преобразуется в интеграл Фурье [3]:

;	(1.29)
.	(1.30)

Здесь выражение (1.29) называется прямым преобразованием Фурье, а (1.30) - обратным. Функция G(w) (спектральная характеристика) комплексная величина, которую можно рассматривать отдельно в виде амплитудной и фазовой характеристик:

.

(1.31)

Отметим вначале свойства этой функции. Она четная: G(w)=G(-w). Модуль G(w) неотрицателен в любом частотном диапазоне. Наконец, она ограничена по частоте:

.

(1.32)

Справедливость последнего соотношения будет ясна из дальнейшего изложения.

В математике интеграл Фурье рассматривают как линейный оператор, переводящий колебание (функцию) из временной области в частотную на комплексную плоскость и обратно. С практической точки зрения определяют физический смысл спектральной характеристики с помощью теоремы Парсеваля [3], определяющей энергию колебания через временные и частотные характеристики:

.

(1.33)

Исходя из (1.33), можно вычислить мощность колебания в полосе частот:

.

(1.34)

Существует еще одно применение теоремы Парсеваля - определение практической длительности импульсов и практической верхней частоты _в :

; .

(1.35)

Здесь m - доверительный коэффициент, как в (1.11).

Например, определим практическую длительность экспоненциального импульса U(t)=e^-t . Примем m=0.9. Тогда

.

(1.36)

Отсюда e^-2t =0.1 или

Кроме указанной теоремы Парсеваля, существуют и другие теоремы о спектрах. Наиболее важны из них следующие:

1. Теорема линейности: спектр линейной комбинации колебаний U(t)=aU₁(t)+bU₂(t) равен линейной комбинации спектров: .

2. Теорема об изменении масштаба времени: сжатие по времени соответствует растяжению по частоте и наоборот:.

Здесь F - оператор Фурье (прямое преобразование).

3. Теорема о дифференцировании: .

4. Теорема об интегрировании: .

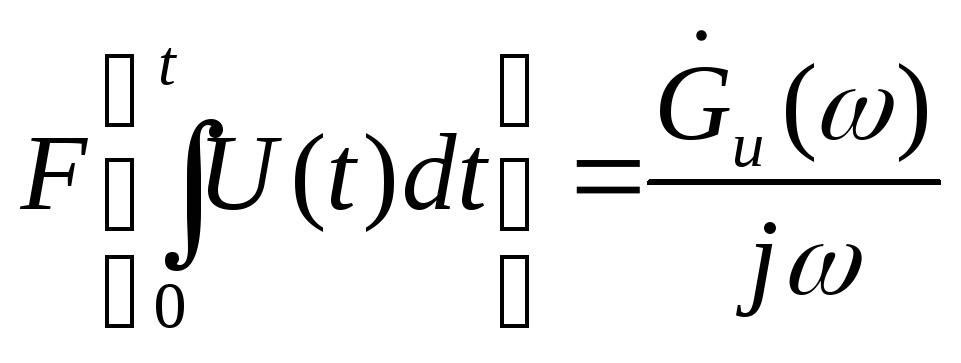Последние две теоремы имеют большое значение при анализе линейных цепей (линейными называются звенья, описываемые обыкновенными дифференциальными уравнениями). Теорема линейности позволяет анализировать суперпозиции двух и более сигналов, а теорема 2 отражает наиболее фундаментальное свойство спектральных преобразований: ширина спектра пропорциональна скорости изменения сигналов.

В заключение отметим наиболее важные причины распространения спектрального анализа. Во-первых, чисто мировоззренческая причина. Любое перемещение физического тела в пространстве можно представить совокупностью двух видов движений: прямолинейного и вращения. Если в качестве одной из координат движения принять поступательное изменение времени, то проекция вращающейся точки на эту ось даст гармоническое колебание. Этим определяется сравнительная легкость представления спектрального анализа. Во-вторых, с математической точки зрения интеграл и производная от тригонометрической функции дают тоже тригонометрическую функцию, что упрощает анализ. И наконец, существует фундаментальное соотношение, связывающее спектр входного и выходного колебаний:

.

(1.37)

Здесь _x()- спектральная характеристика колебания на входе линейного звена с частотной характеристикой K(j), _y() - спектр выходного колебания. Соотношение (1.37) является основой для целого раздела теории сигналов - анализа линейных звеньев в частотной области [10].

Вкратце рассмотрим некоторые другие используемые на практике разложения в ряды, отличающиеся функциями разложения.

Полиномы Чебышева были предложены русским математиком П.Л.Чебышевым как решение задачи об оптимальной аппроксимации произвольной гладкой функции на интервале [-1;1]. Общая форма записи полинома Чебышева имеет вид [15]:

,

(1.38)

где T - полином Чебышева порядка n.

Н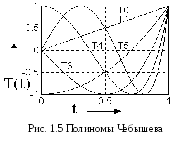есмотря на то, что полученное выражение громоздко, существует простая рекуррентная формула для вычисления полинома порядка n+1 через полиномы степеней n и n-1:

Tn+1(t)=2tTn(t)-Tn-1(t),

(1.39)

причем T₀=1, T₁=t. Отсюда T₂ =2t² -1, T₃ =4t² -3t и т.д.

Графики первых пяти полиномов на интервале [0,1] приведены на рис. 1.5. Из них видно, что полиномы четных порядков четны, а нечетных - нечетны. Количество экстремумов полинома на единицу меньше порядка n. Предполагается, что вне этого интервала полиномы не определены.

Полиномы Чебышева ортогональны с весом, причем весовая функция:

(1.40)

Существует множество приложений использования полиномов Чебышева в задачах интерполяции и оптимизации [2.8], но непосредственное разложение функций в ряды используется редко.

Функции Бесселя 1 рода образуются как решение цилиндрических дифференциальных уравнений вида:

.

(1.41)

Решение представляется неаналитическими функциями, которые выражаются бесконечными суммами вида:

;	(1.42)
.	(1.43)

Здесь ₀(t), _s(t) - функции Бесселя 1 рода соответственно порядка 0 и s. Общий вид функций приведен на рис. 1.6. Из графиков видно, что функции и нечетных порядков начинаются в нуле, а с увеличением порядка они имеют меньшую амплитуду и затухают быстрее. Это обстоятельство будет использовано в дальнейшем.

Ф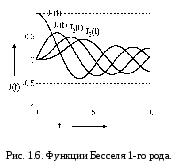ункции Бесселя также ортогональны с весом t:

.

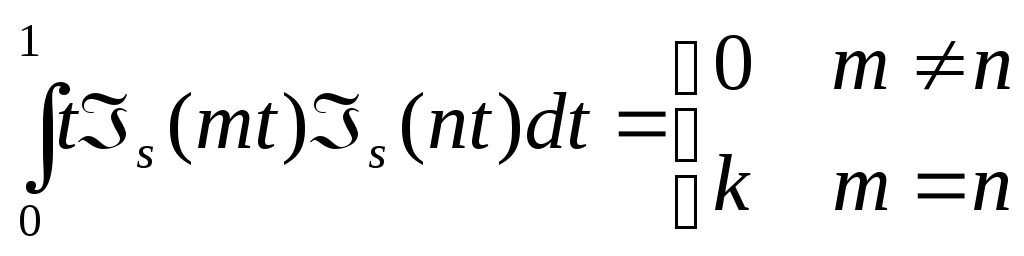(1.44)

Как функции разложения в ряды, они практически не используются из-за громоздкости вычислений по формулам (1.42), (1.43) (хотя, как можно убедиться, ряды очень быстро сходятся из-за наличия факториалов в знаменателях), зато используются как производящие при представлении функций вида sin/cos(rsin/cost) (запись вида sin/cos означает, что в этом месте может находиться функция sin или cos):

	(1.45)
	(1.46)
	(1.47)
	(1.48)

Полиномы Лагерра являются частными решениями одного вида дифференциальных уравнений 2 порядка и определяются из выражения:

.

(1.48)

Отсюда L₀(t)=e^te^-t =1; L₁(t)==t-1.

Рекуррентная формула

Ln+1(t) = (t-2n-1)Ln(t)-n2Ln-1(t).

(1.49)

Из (1.49) L₂(t)=(t-2-1)L₁(t)-1² = t² - 4t + 2 и т.д.

Полиномы Лагерра ортогональны с весом e^-t на интервале [0,]:

(1.50)

Их можно использовать как функции разложения на полубесконечном интервале.

Функции Котельникова вводятся при дискретизации непрерывных колебаний (об этом речь пойдет ниже). Они имеют вид:

.

(1.51)

З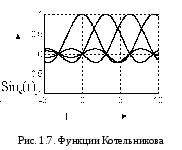десь t- шаг по времени (обычно t=const). Графики функций приведены на рис.1.7. Из графиков видно, что во всех точках, кратных t, (t=mt, m-целое) все функции, кроме одной, обращаются в 0, а единственная ненулевая функция, для которой t=kt, имеет значение U(kt). Это позволяет утверждать, что система функций Котельникова ортогональна в таких точках, называемых узлами.

Недостаток функций состоит в том, что они бесконечны в обе стороны (сравните, например, с функциями Бесселя), а это значит, что при разложении в ряд нужно знать все точки u(t) на бесконечном интервале (или при ограниченности интервала потребуется предсказывать значения u(t)).

Функции Уолша относятся к классу дискретных и являются обобщением функций Родемахера:

,

(1.52)

где sign(z) - знаковая функция.

Недостатком функций Родемахера является то, что все они четны. Известно, что линейная комбинация четных функций может дать только четные функции, следовательно, не любое колебание можно представить функциями Родемахера. Функции Уолша устраняют этот недостаток.

Существует два алгоритма реализации этих функций, Адамара (had(k,x))и Пэли (pal(k,x)). Согласно первому, существует рекурсивная процедура получения матрицы порядка k+1 через матрицу порядка k:

.

(1.53)

Если матрица H₀=|+1|,то H₁=. Продолжая эту процедуру, можно написать, например, матрицу H₃ в виде (оставлены только знаки)

H3=	+	+	+	+	+	+	+	+	0	(1.54)
	+	-	+	-	+	-	+	-	1
	+	+	-	-	+	+	-	-	2
	+	-	-	+	+	-	-	+	3
	+	+	+	+	-	-	-	-	4
	+	-	+	-	-	+	-	+	5
	+	+	-	-	-	-	+	+	6
	+	-	-	+	-	+	+	-	7

Согласно алгоритма Пэли, матрица порядка k+1 образуется из матрицы порядка k двукратным повторением каждой строки порядка k, после чего к первой из полученных строк приписывается эта же строка, а ко второй - ее инверсия. Тогда матрица третьего порядка примет вид:

P3=	+	+	+	+	+	+	+	+	0	(1.55)
	+	+	+	+	-	-	-	-	1
	+	+	-	-	+	+	-	-	2
	+	+	-	-	-	-	+	+	3
	+	-	+	-	+	-	+	-	4
	+	-	+	-	-	+	-	+	5
	+	-	-	+	+	-	-	+	6
	+	-	-	+	-	+	+	-	7

Нетрудно заметить, что матрица (1.54) состоит из тех же строк, что и (1.55), только они переставлены местами.

На рис 1.8 представлено семейство функций Уолша-Адамара для N=8=2³. Нетрудно определить способ их изображения. Для этого интервал времени, равный периоду функции U(t), разбивают на N=2³ равных участков в соответствии с матрицей вида (1.54) или (1.55) и на каждом из участков изображают уровень +1 или -1.

В некоторых приложениях [12] пытаются провести аналогию с рядами Фурье, для чего матрицы H ранжируют по признаку количества пересечений графиком оси времени (количество пересечений при этом называют частостью). Например, строки матрицы (1.54) будут ранжированы в таком порядке: 0,4,6,2,3,1,5,7, предполагая при этом, что функция 0 соответствует постоянной составляющей, 4-первой гармонике, синусной составляющей, 6-первой гармонике, косинусной составляющей и т.д. Последние две функции нерегулярные и располагаются в конце списка. Диаграммы, построеные по такому принципу, сходны со спектром ряда Фурье и лежат в основе так называемого секвентного анализа (по аналогии со спектральным анализом).

Определим теперь свойства полученных функций. Это семейство всегда состоит из N функций (соответствующая диаграмма представлена N спектральными линиями) и образует замкнутую и полную систему (в данном случае замкнутость означает, что произведение двух любых функций даст третью из того же множества).

Любая функция с номером, отличным от 0, имеет нулевую постоянную составляющую, а все семейство их ортогонально.

Функции Уолша в последнее время используются очень широко в связи с развитием цифровой техники. Это связано с тем, что семейство вида (1.54) легко генерируется цифровыми элементами, а вычисление коэффициентов разложения по формуле (1.16) проходит очень быстро, так как интеграл заменяется на сумму из N членов, а умножение на функцию had эквивалентно изменению (сохранению) знака сомножителя.

Колебания, полученные из рядов Уолша по формуле (1.6), дают кусочно-ступенчатые функции, в которых количество "ступенек" на периоде равно N, а амплитуда i-той ступеньки пропорциональна производной исходного колебания в этот момент времени.

Кроме спектральных представлений сигналов, широко используются их описания с использованием теории вероятностей; сигнал можно представить в виде случайного процесса (случайной функции) [11]. Случайный процесс - это обобщение случайной величины при рассмотрении ее с введением дополнительной координаты времени. Классическим методом описания случайного процесса является ансамбль реализаций - совокупность случайных функций, наблюдаемых одновременно на выходах множества однотипных объектов. В каждый момент времени t₀ можно получить совокупность значений для каждой случайной функции (это называется сечением процесса в момент t₀), которая является случайной величиной.

Определим основные понятия теории вероятностей из раздела случайные величины. Существует два способа описания случайных величин: с помощью плотности распределения вероятностей f(u) и функции распределения F(x). Перечислим их свойства.

Для плотности распределения:

f(u)0|u	(положительная определенность);
	(ограниченность);
	(нормировка);
	(интервальная вероятность).

Аналогично для функции распределения:

F(-)=0; F()=1	(граничные значения);
F(b)F(a) при b>a	(монотонность);
(aP<b)=F(b)-F(a)	(интервальная вероятность).

Из последнего соотношения вытекает

.

Применительно к плотности распределения может быть использована формула Байеса:

f2(a,b)=f(a)f2(b|a)=f(b)f2(a|b),

(1.56)

где f₂(a,b)- двумерная плотность, f₂(b|a) - условная плотность распределения вероятности.

Часто вместо указанных функций используют числовые характеристики - упрощенное описание случайных величин. Перечислим наиболее распространенные.

Математическое ожидание m_u(M[u]) - среднее значение случайной величины. Для дискретных величин величин оно определяется по формуле:

M[u]=mu=ui p(ui),

(1.57)

где N-количество различных состояний случайной величины, p(u_i)-вероятность ее i-го состояния.

Для непрерывных величин

.

(1.58)

Из свойств математического ожидания наиболее характерны два:

M[cu]=cm_u (константа выносится за знак математического ожидания);

M[uv]=m_u  m_v.

Дисперсия D[u]= характеризует отклонение случайной величины от среднего значения:

.

(1.59)

(Здесь и далее выражения для дискретных величин будем опускать, поскольку они аналогичны). Выделим два свойства дисперсии:

(всегда сумма);

D[cu]=c².

Перечислим менее употребимые характеристики.

Мода-M₀[u]-наиболее вероятное значение случайной величины:

f(u=M0[u])=max.

(1.60)

Если плотность распределения имеет несколько локальных максимумов, распределение называется полимодальным, если имеет минимум - антимодальным (равномерное распределение моды не имеет).

Медиана Me[u] - значение случайной величины, делящее область ее определения на две равновероятные части:

P(u<Me[u])=p(uMe[u])=0.5.

(1.61)

Асимметрия As[u] характеризует несимметричность кривой распределения:

.

(1.62)

В отличие от дисперсии, асимметрия нормирована (безразмерна).

Эксцесс Ex[u] характеризует отклонение распределения от нормального (гауссовского):

.

(1.63)

В этом выражении 3 появилась вследствие того, что центральный момент четвертого порядка для нормального распределения равен 3.

Кроме нормального и равномерного, наиболее часто используются распределения: треугольное (Симпсона), Релея, Пуассона, Бернулли (дискретные). Достаточно подробное описание распределений и их числовых характеристик приведено в [ 14].

Приведем пример. Случайная выборка по фазе в синусоидальном сигнале с амплитудой a приводит к так называемому распределению арккосинуса, плотность распределения которого

.

Г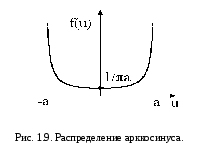рафик f(u) приведен на рис.1.9. Из него видно, что это антимодальное симметричное распределение, для которого минимум при u=0: f_min=1/a. Поскольку распределение симметрично, математическое ожидание совпадает с модой и медианой. Дисперсия D[u]=a²/2 , что соответствует действующему значению этого колебания. Плотность распределения

.

Отсюда понятно и название распределения.

Случайные процессы во времени описываются в основном тремя функциями: математическим ожиданием, дисперсией и корреляционной функцией:

	(1.64)
	(1.65)
	(1.66)

Здесь f₂(u₁,u₂;t₁,t₂)-двумерная плотность распределения вероятности. В большинстве случаев рассматриваются так называемые стационарные процессы. Стационарными называются процессы, для которых плотности распределения не зависят от выбора начала отсчёта. Для них математическое ожидание и дисперсия не зависят от времени, а корреляционная функция зависит только от разности моментов отсчета =t₂-t₁ .

О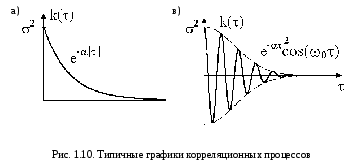 пределим теперь корреляционную функцию. Она выражает взаимосвязь между значениями случайного процесса при разности между моментами отсчета, равной . Из этого определения вытекают и свойства функции. Наибольшей будет взаимосвязь при =0 (k_uu(0)= ), наименьшей - при t (k_uu()=0). Поскольку взаимосвязь симметрична, функция четна(k_uu()=k_uu(-)). Типичные графики корреляционных функций приведены на рис.1.10,a и b.

Возможно представление случайных процессов не только во временной, но и в частотной области. Для этого Н. Винер и П. Хинчин применили интеграл Фурье к корреляционным функциям [25]:

.

(1.67)

Полученная функция S_uu() называется спектральной плотностью мощности и определяет распределение мощности случайного процесса по частоте. Эта функция четна и ограничена по частоте (S()=0). Интеграл от спектральной плотности равен мощности сигнала в заданном частотном диапазоне:

;	(1.68)
.	(1.69)

Выражение (1.69) определяет полную мощность сигнала.

П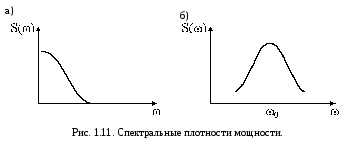 оскольку и k(), и S() четны, часто при изображении графиков ограничиваются правой полуплоскостью. На рис.1.11. показаны графики S(), соответствующие корреляционным функциям рис.1.10,a и b.

Из выражений (1.68) и (1.69) можно определить практическую ширину спектра случайного сигнала:

:

(1.70)

где m - доверительный коэффициент.

Практически это сводится к вычислению неопределенного интеграла в левой части (1.70) с последующим решением полученного уравнения относительно _b .

Приведем некоторые наиболее характерные разновидности случайных процессов.

1.Пуассоновский процесс. Такого вида процессы используются при описании динамики систем массового обслуживания и в задачах надёжности [2.6]. Корреляционная функция имеет вид

.

Вид функции приведён на рис. 1.10,а.

Спектральная плотность мощности

.

( см. рис. 1.11,а ). Использование выражения (1.70) даёт следующее уравнение для вычисления _b :

.

Отсюда следует, что увеличение  приводит к сжатию корреляционной функции и растяжению спектральной плотности, что, в свою очередь, увеличивает граничную частоту _b.

2.Гауссовский процесс - одна из наиболее встречающихся разновидностей случайных сигналов. Для него

.

Применение выражения (1.70) даёт неберущийся интеграл, который можно свести к функции Лапласа [9].

3. Белый шум - наиболее часто используемая модель флуктуационной помехи. Это "абсолютно случайный" сигнал, для которого корреляционная функция вырождается в -функцию ( функцию Дирака ): . Это означает, что взаимосвязь между значениями процесса отсутствует при любых, сколь угодно малых, значениях . Спектральная плотность не зависит от частоты. Такого рода сигнал физически нереализуем, так как требует бесконечно большой мощности, поэтому спектр шума ограничивают пределами спектра полезного сигнала.

4. Телеграфный сигнал - простейшая модель импульсного сигнала. Он представляет собой бесконечную последовательность разнополярных прямоугольных импульсов, следующих с постоянным периодом, но со случайной длительностью (см. рис. 1.12). Для него

;

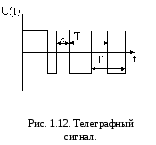
Верхняя частота по формуле (1.70) не вычисляется аналитически, поэтому приближённо считают .

5. Узкополосный сигнал. Это наиболее часто используемая модель сигнала в радиотехнике. Корреляционная функция имеет описание вида

,

где R() - корреляционная функция низкочастотного процесса.Вид функции K() приведен на рис. 1.10,б а соответствующая ей спектральная плотность на рис. 1.11,б. Выражение (1.70) для определения _b приобретает вид

.
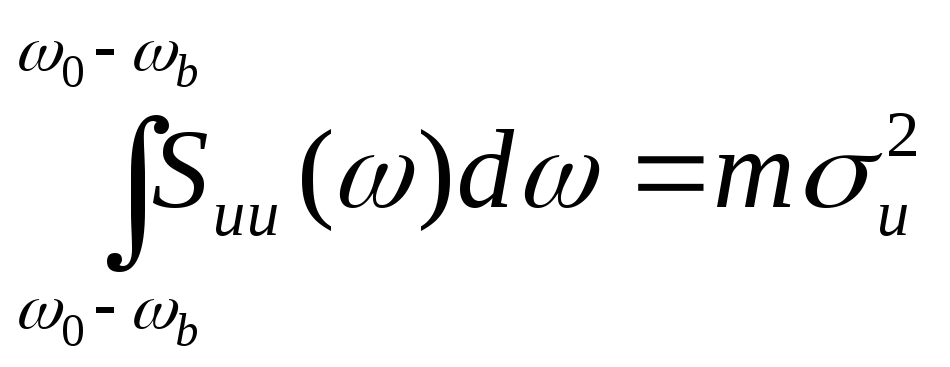
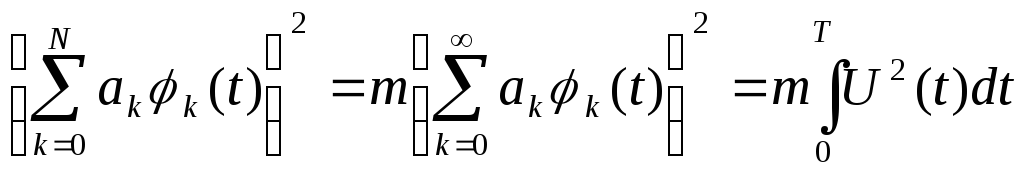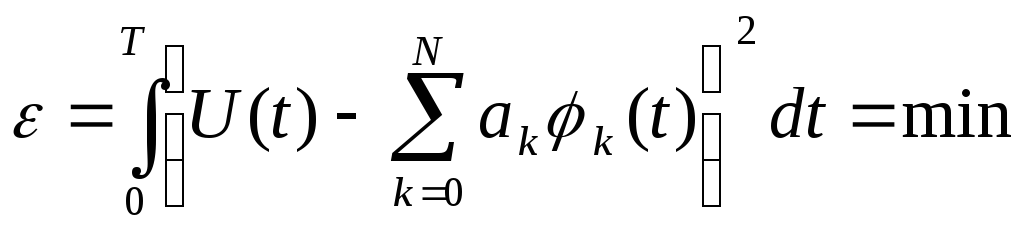
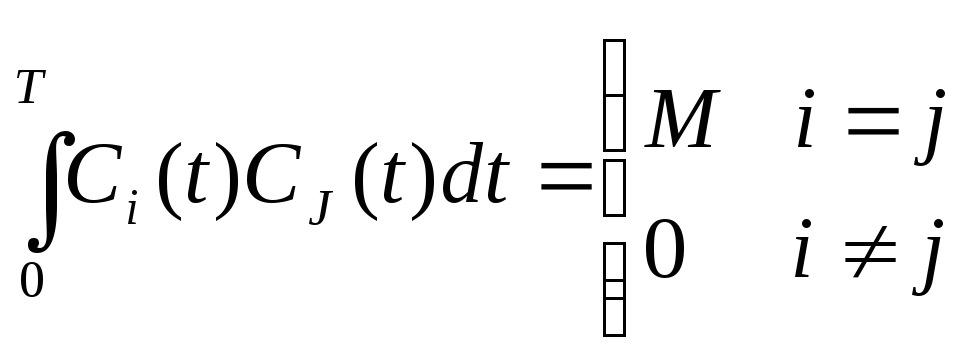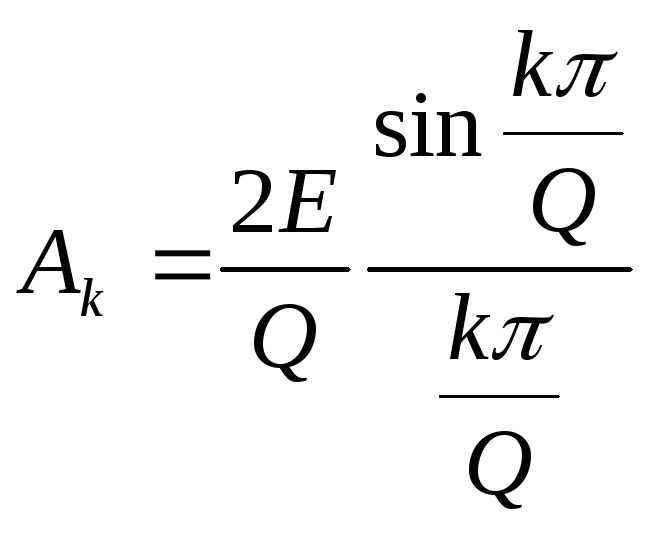
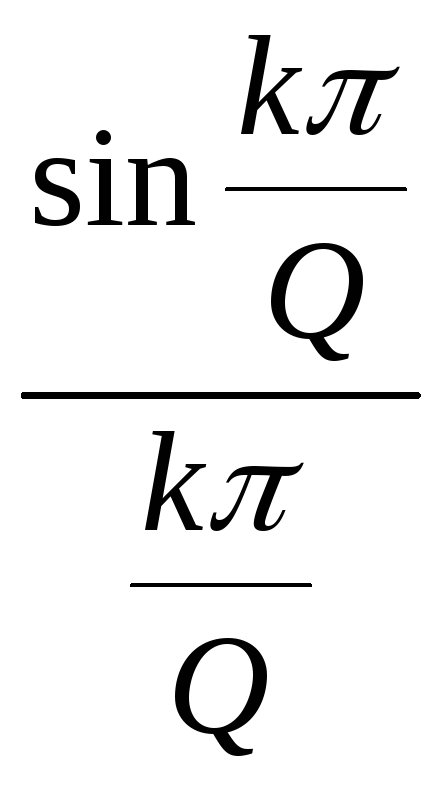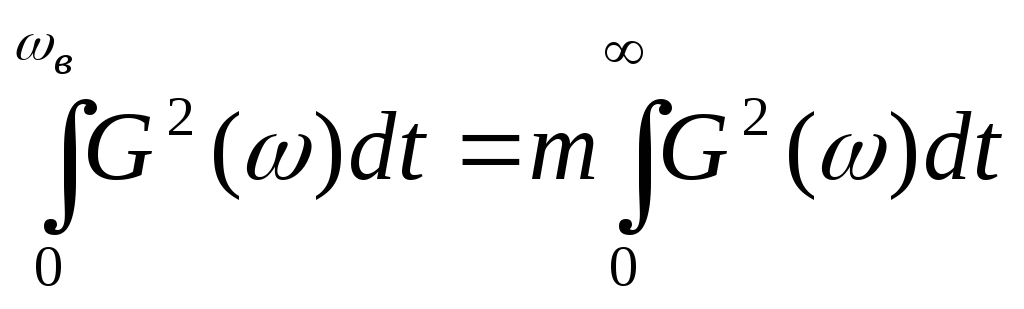
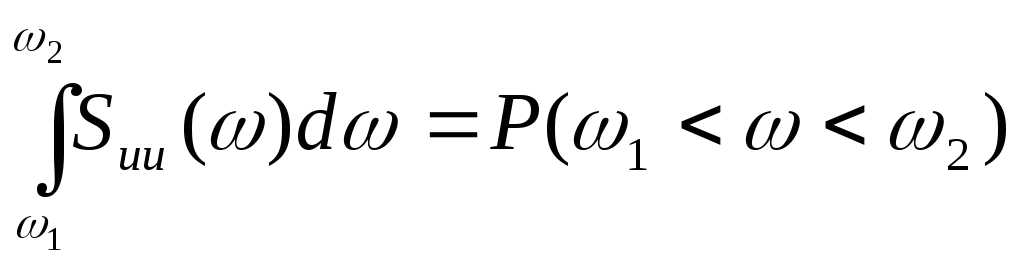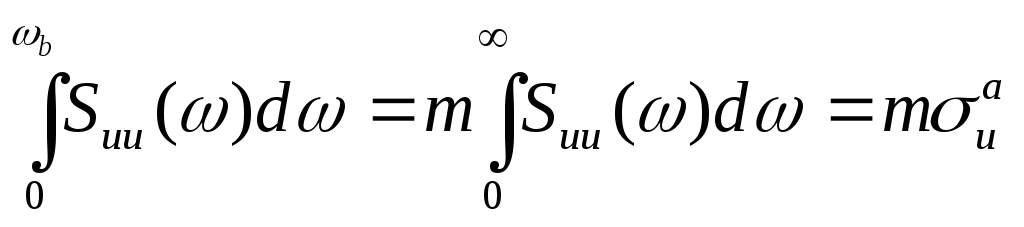