Размещение частиц по ячейкам

К основным понятиям комбинаторики можно подойти, рассматривая задачу о размещении частиц (предметов, объектов, шаров) по ячейкам (ящикам, урнам). При этом частицы могут быть различимыми и неразличимыми, в свою очередь ячейки могут независимо от частиц классифицироваться по виду, вместимости и т.п.

Различимые частицы и ячейки

Поставим вопрос о числе способов размещения n различных частиц по k различным ячейкам. Первая частица может быть помещена в любую из k ячеек, поэтому для нее есть k вариантов размещения; вторая частица также может быть помещена в любую из k ячеек, поэтому для нее существует также k вариантов размещения и так, очевидно, для всех частиц. Следовательно, для всех n частиц число возможностей равно kⁿ.

Пример. Рассмотрим размещения частиц a, b по трем ячейкам

1	|ab| - | - |	4	| a | b | - |	7	| b | - | a |
2	| - |ab| - |	5	| b | a | - |	8	| - | a | b |
3	| - | - |ab|	6	| a | - | b |	9	| - | b | a |

Число способов размещений n различных частиц по k ячейкам совпадает с числом выборок объема n из k различных предметов и равно kⁿ. Это число называют числом размещений с повторениями или перестановками с возвращением. Таким образом, число размещений с повторениями или перестановок с возвращением из k no n равно U(k,n) = kⁿ.

Рассмотрим теперь число размещений n различных частиц по k ячейкам при условии, что в каждой ячейке может располагаться не более одной частицы. Первая частица может быть помещена в любую из k ячеек; вторая частица может быть помещена в любую из оставшихся незанятых (k – 1) ячеек; третья в любую из (к - 2) ячеек и так далее; для последней частицы остается (k – n + 1) возможностей. Всего вариантов размещения n различных частиц по k ячейкам по одной частице в ячейке равно:

.

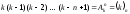Эта формула совпадает естественно с формулой предыдущего пункта при k = n, n = r.

Теперь легко понять, что число размещений n различных частиц по ячейкам при условии, что в i-ой ячейке помещено n_i частиц, 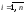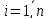, n₁ + n₂ + ... + n_k = n, равно

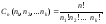
Так как общее число размещений n частиц по k ячейкам, равное kⁿ, складывается из всевозможных размещений, для которых справедливо n₁ + n₂ + ... + n_k = n, то очевидна справедливость следующего соотношения:

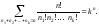
Это соотношение совпадает с ранее полученным.

Одинаковые частицы

Исследуем вопрос о числе размещений n неразличимых частиц по k ячейкам. Для примера рассмотрим случай n = 3, k =3.

1	|•••| - | - |	4	| - | - |•••|	7	| • | - |••|
2	| • |••| - |	5	|••| • | - |	8	| - |••| • |
3	| - |•••| - |	6	|••| - | • |	9	| - | • |••|
10	| • | • | • |

Для решения задачи будем представлять частицы точками, а ячейки как промежутки между черточками. Различные размещения тогда соответствуют различным взаимным расположениям точек и черточек, при этом число черточек равно k-1. Любые размещения всегда соответствуют всевозможным расположениям n точек и

(k-1) черточек (перегородок между ячейками без учета двух крайних). Отсюда вытекает, что число размещений n неразличимых частиц по k ячейкам равно числу различных перестановок из n+k-1 элементов, из которых n одинаковы между собой и (k-1) одинаковы между собой. Число таких перестановок, очевидно, равно

.

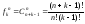Таким образом, число размещений n одинаковых частиц по k ячейкам равно числу сочетаний с повторениями из k по n. Очевидно также, что это число равно числу решений уравнения

n₁ + n₂ + ... + n_k = n в целых неотрицательных числах n_i ≥ 0, .

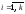
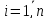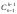
Условие отсутствия пустых ящиков приводит к ограничению: каждая черточка должна располагаться только между точками. Всего имеется (n-1) промежутков между точками, в них нужно поместить (k-1) черточек. Это можно сделать 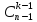способами. Таким образом, число способов размещения n одинаковых частиц по k ячейкам при отсутствии пустых ячеек равно:

.

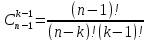
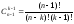Посмотрим теперь каково число способов размещения n одинаковых частиц в k ячейках по одной в ячейке, разумеется, это возможно при n ≤ k. Искомое число способов равно количеству вариантов выбора n ячеек (в которые и будут помещены n частиц) из всех k ячеек:

.

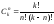
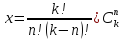Этими рассуждениями получена новая интерпретация для комбинаторного понятия числа сочетаний. Напомним, что в предыдущем пункте было установлено, что число сочетаний есть число разделений k различных предметов на две группы, одна из которых содержит n предметов, а другая (k-n) предметов (в обозначениях данного пункта). Число сочетаний есть также число размещений k различных частиц в два ящика, причем в первом ящике располагается n частиц, а во втором - (k-n) частиц.