
- •Тема 1 Лінійна алгебра Системи лінійних алгебраїчних рівнянь (слар)
- •Система трьох лінійних рівнянь з трьома невідомими
- •Тема 2 Визначники другого і третього порядків та їх властивості
- •Основні властивості визначників 3-го порядку
- •Тема 3 Матриці
- •Лінійні дії над матрицями
- •Множення матриць
- •Властивості множення матриць
- •Визначник добутку матриці
- •Обернена матриця
- •Розв’язування слар матричним способом
- •Тема 2 Векторна алгебра Вектори
- •Розклад даного вектора за напрямками на прямій, на площині і в просторі
- •Лінійна залежність і лінійна незалежність системи векторів
- •Декартова прямокутна система координат
- •Лінійні операції над векторами
- •Перехід вектора до нового базису
- •Умова колінеарності двох векторів
- •Поділ відрізка у даному співвідношенні
- •Скалярний добуток векторів
- •Довжина вектора
- •Косинус кута між векторами
- •Умова ортогональності векторів
- •Проекція вектора на вектор
- •Фізичний зміст скалярного добутку
- •Векторний добуток векторів
- •Застосування векторного добутку
- •Мішаний добуток трьох векторів
- •1. Алгебрична форма комплексного числа.
- •2. Тригонометрична форма комплексного числа.
- •3. Показникові форма комплексного числа. Формули Ейлера.
- •4. Деякі застосування комплексних чисел.
- •Похідна функції
- •1. Визначення похідній, її геометричний і механічний зміст
- •Геометричний зміст похідної
- •1.2. Механічний зміст похідної
- •2. Найпростіші правила знаходження похідній
- •2.1. Похідна як функція
- •3. Похідна зворотної функції
- •4. Похідні елементарних функцій (табличні похідні)
- •5. Похідна складної функції (композиції)
- •6. Диференціал
- •6.1. Інваріантість форми диференціала
- •Геометричний зміст диференціала
- •6.3. Диференціал суми, добутку, частки
- •7. Похідні й диференціали вищих порядків
- •7.1. Неінваріантість форми диференціалів більше високого порядку
- •8. Основні теореми про диференційовані на відрізку функції
- •9. Формула тейлора і її застосування
- •Подання основних елементарних функцій по формулі тейлора
- •1. Зростання й убування функції. Екстремуми. Найбільше й найменше . Значення функції
- •1.1. Зростання й убування функції
- •2. Точки екстремуму функції
- •1.3. Найбільше й найменше значення безперервної на відрізку функції
- •2. Опуклість нагору й униз, точки перегину
- •3. Асимптоти кривих
- •4. Дослідження функцій і побудова їхніх графіків
- •5. Задачі на екстремум
1. Зростання й убування функції. Екстремуми. Найбільше й найменше . Значення функції
1.1. Зростання й убування функції
Визначення 1. Нехай функція f(x) визначена на інтервалі (а,b). Кажуть, що функція f(x) зростає (убуває) у точці х0 C (а,b), якщо існує δпро > 0 таке, що s(xo,δo) З (а,b), і для будь-якого h, що задовольняє нерівності 0 < h <δo, виконується нерівність
![]() (1),
(1),
(2)
Визначення 2. Функція f(x), певна на інтервалі (а,b), називається зростаючої (убутної) на інтервалі (а,b), якщо для будь-яких х1, x2 € (а,b) таких, що х1 < x2, виконується нерівність
![]() (3),
(3),
(4)
Запишемо визначення зростання функції на інтервалі (а, b) мовою предикатів і кванторів:
![]()
ТЕОРЕМА 1
Для того щоб функція f(х), певна на інтервалі(а,b), була зростаючої (убутної), необхідно й досить, щоб вона була зростаючої (убутної) у кожній точці інтервалу.
Зауваження. Незважаючи на гадану очевидність і простоту, доказ достатності надзвичайно трудомістко й вимагає старанності й акуратності в міркуваннях.
ТЕОРЕМА 2 (Достатні умови зростання функції в точці й на інтервалі)
Якщо функція f(х) диференційована в точці x0 € (а,b) і f'(x0)>0 (f'(xo)<0), то функція f(x) зростає (убуває) у точці хо.
Якщо функція f(x)диференційована на (а,b) і в кожній точці х € (а,b) f'(x) > 0 (f'(x) < 0), то функція f(x) зростає (убуває) на інтервалі (а,b).
Ясно, що друга частина теореми — наслідок першої частини й теореми 1. Доведемо першу частину теореми для випадку f'(x0) > 0.
Ми знаємо, що з визначення похідної функції в точці треба, що існує δпро > 0 таке, що s(xo,δo) З (а,b), і в s(xo, δо) виконується формула
![]()
Виберемо 0<δ1≤ δпро таке, що
![]()
Тоді
для всіх х
€
s(xo,δo)
![]() f>0
для
f>0
для
![]() x
>0 і
x
>0 і
![]() f
< 0 для
f
< 0 для
![]() х
< 0,
а із цього треба, що якщо h
таке,
що 0 < h≤
δпро,
те
х
< 0,
а із цього треба, що якщо h
таке,
що 0 < h≤
δпро,
те
![]()
т. е. зростання функції f(x) у точці x0, коли f'(xo) > 0, доведено. Убування функції f(х) у точці хо, коли f'(х0) < 0, доводиться аналогічно.
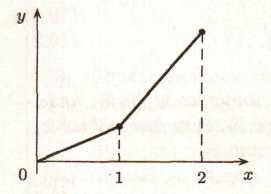
Зауваження. Умови теореми 2 є лише достатніми. Дійсно, функція f(x) = x3 у точці х = 0 зростає. а f'(0) = 0.
Точками зростання безперервної функції на (а,b) можуть бути також точки, у яких похідна не існує; дійсно, розглянемо функцію, певну на (0,2) правилом
![]()
Її графік зображений на мал.1.
Ясно, що вона безперервна на (0,2), зростає на (0,2), значить (теорема .1), зростає в кожній точці інтервалу (0,2), однак у точці х = 1 вона не є диференційованою (подумайте чому?).
2. Точки екстремуму функції
Ми вже дали визначення точок локального максимуму й мінімуму, назвавши їхніми точками локального екстремуму, і довели теорему, що дає необхідна умова того, що точка є точкою локального екстремуму диференційованої функції, що складалося у зверненні до нуля похідної.
Ця теорема дала ключ до знаходження множини точок, «підозрілих» на екстремум (ці точки ще називають критичними точками для функції f). Ми зрозуміли, що критичними точками для функції, безперервної на (а,b), є точки, у яких похідна функції дорівнює нулю або не існує.
Ясно, що критична точка є точкою локального максимуму, якщо при переході аргументу через неї відбувається зміна характеру монотонності зі зростання на убування, і точкою локального мінімуму, якщо при переході через неї відбувається зміна монотонності з убування на зростання.
Ясно, що якщо функція f(x) така, що точка x0 — критична для f(х) і існує δo > 0 таке, що для будь-якого х € s’-(xo,δo) f'(x) > 0 і для будь-якого х € s’+(xo,δo) f'(x)< 0, точка хо є точкою локального максимуму; а якщо для будь-якого х € s’-(xo,δo) f'(x)<0 і для будь-якого х € s’+(xo,δo) f'(x)<0, то точка хо є точкою локального мінімуму.
Якщо ж при переході через критичну точку не відбувається зміни характеру монотонності, то точка x0 не є точкою локального екстремуму.
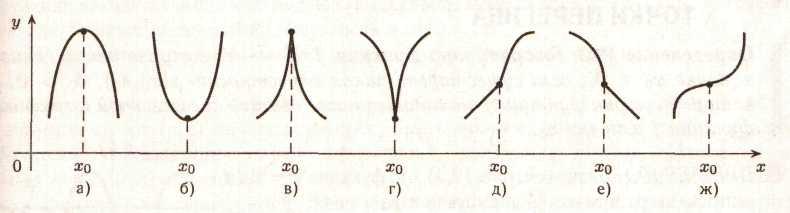
На мал. 2. а)-ж.) наведені можливі ситуації, які можуть бути в критичних точках.
Випадки:
а) f'(х0)
=
0,
![]() —
х0
- точка
максимуму;
—
х0
- точка
максимуму;
б) f'(x0)
= ПРО,
![]() —
х0
-точка
мінімуму;
—
х0
-точка
мінімуму;
в) f'(х0)
не існує,
![]() —
х0
-точка
максимуму;
—
х0
-точка
максимуму;
г) f'(х0)
не
існує,
![]() —
х0
-точка
мінімуму;
—
х0
-точка
мінімуму;
д) f'(х0)
не існує,
![]() —
х0
не
є точкою екстремуму;
—
х0
не
є точкою екстремуму;
е) f'(х0)
не існує,
![]() —
х0
не
є точкою екстремуму;
—
х0
не
є точкою екстремуму;
ж)
f'(х0)
![]() —
х0
не є точкою екстремуму.
—
х0
не є точкою екстремуму.
