1.2. Структуры данных для предоставления графов

Информацию о графах и орграфах можно хранить двумя способами:

1. в виде матрицы примыканий;

2. в виде списка примыканий.

Матрица примыканий обеспечивает быстрый доступ к информации о ребрах графа. Однако, если в графе мало ребер, то эта матрица будет содержать гораздо больше пустых клеток, чем заполненных.

Длина списки примыканий пропорциональна числу ребер в графе, однако, при пользовании списком, время получения информации о ребре увеличивается.

Таким образом, ни один из этих методов не превосходит другой заведомо.

Определение.

Матрица примыканий графа с числом вершин записывается в виде двумерного массива размера .

В каждой ячейке этого массива записано число «нуль» за исключением лишь тех случаев, когда из вершины в вершину ведет ребро. Тогда в ячейке записывается «единица».

Более строго это можно записать так:

.

Рассмотрим, как будут выглядеть матрицы примыканий в конкретных примерах.

Пример.

Пусть задан граф следующего вида

.

Матрица примыканий для этого графа принимает вид:

.

Матрица примыкания для неориентированного графа обладает следующими свойствами:

1. на главной диагонали расположены нулевые элементы;

2. матрица примыканий в данном случае является симметрической.

Пример.

Пусть задан орграф следующего вида

.

Матрица примыканий принимает вид:

.

Матрица примыканий дл ориентированного графа обладает следующими свойствами:

1. на главной диагонали расположены нулевые элементы;

2. матрица примыканий является кососимметрической (антисимметрической).

Ячейка матрицы примыканий взвешенного графа или орграфа содержит («бесконечность»), если соответствующее ребро отсутствует.

Во всех остальных случаях ее значение равно весу ребра.

При этом диагональные элементы такой матрицы равны нулю, поскольку переход из вершины в нее саму не стоит ничего.

Рассмотрим пример.

В качестве примера возьмем дорожный граф из Октябрьского района г. Самары (Рисунок 10).

250

Рисунок 10 – Граф дорожной сети Октябрьского района г. Самары. Веса графа указаны в мерах

Для взвешенного графа рисунка 10 матрица примыканий приобретает вид (фрагмент):

.

Полученная матрица является симметрической порядка .

На главной диагонали находятся нули, означающие, что «стоимость перевозки» внутри самого узла теоретически равна нулю.

Предлагается студентам достроить эту матрицу до конца самостоятельно.

Определение.

Список примыканий графа с числом вершин записывается в виде одномерного массива размера , каждый элемент которого представляет собой ссылку на список.

Рассмотрим построение списка примыканий для графа вида

Список примыканий имеет следующий вид:

1.3. Поток на дуге и техническая оснащенность дуги

Введем далее две важные для дальнейшего изложения характеристики дуги графа: поток на дуге и техническую оснащенность дуги .

Определение.

Под потоком в сети понимается количество транспортных средств и (или) пассажиров, перемещающихся в единицу времени по некоторым дугам в сети из пункта отправления в пункт назначения.

Предполагается, что поток на дуге задается неотрицательным действительным числом .

Определение.

Техническая оснащенность дуги определяет любой технический параметр дуги транспортной сети (в том числе пропускную способность дуги).

Техническая оснащенность дуги задается неотрицательным действительным числом .

В большинстве исследований по оптимизации сетей есть еще одно ограничение, согласно которому поток не может превышать пропускную способность дуги .

В настоящем курсе мы это ограничение использовать не будем.

Вместо этого предположим, что длина дуги есть функция технической оснащенности и потока дуги:

.

Эта функция обладает следующими свойствами:

; ; при .

Прокомментируем эти условия.

1. Зависимость при имеет следующий вид (Рисунок 11).

Рисунок 11 – Зависимость длины дуги от технической оснащенности дуги

Предположим, что под понимается разрешенное число полос движения транспорта по некоторой дуге сети . Тогда эту ситуацию можно интерпретировать следующим образом. Пусть для определенности в данном случае поток равен транспортным единицам. Тогда, рассматривая длину дуги для двух значений технической оснащенности и , в результате получим (Рисунок 12).

Рисунок 12 – Распределение транспортных средств при ;

– интервал движения

Из анализа рисунка 12 следует очевидный вывод:

.

2. Далее рассмотрим зависимость при (Рисунок 13).

Рисунок 13 – Зависимость длины дуги от потока

Предположим для определенности, что (условно разрешена одна полоса движения транспорта). Тогда получим следующий результат (Рисунок 14).

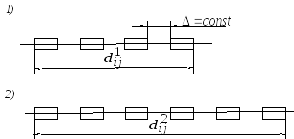
Рисунок 14 – Распределение транспортных средств при ;

– интервал движения

Непосредственно из анализа рисунка 14 получаем тривиальный результат:

.