2. Формула полной вероятности

Пусть интересующее нас событие может наступить или не наступить с одним из ряда несовместных событий , составляющих полную группу событий. События такого рода обычно называются гипотезами. Вероятность всех гипотез известны, т.е. даны . Известны также условные вероятности наступления события при осуществлении каждой из указанных гипотез, т.е. . Тогда вероятность наступления интересующего нас события определяется по формуле полной вероятности:

(7.10)

Пример 7.4. На склад поступили детали с трёх станков. На первом станке изготовлено 50% деталей от их общего количества, на втором- 30% и на третьем —20%,причём на первом станке было изготовлено 85% деталей первого сорта, на втором —80% и на третьем — 75%.Какова вероятность того, что взятая наугад деталь окажется первого сорта?

Решение:

Пусть событие состоит в том, что взятая наугад деталь оказалась первого сорта. Возможны три гипотезы: – деталь изготовлена на первом станке, ; – деталь изготовлена на втором станке, ; – деталь изготовлена на третьем станке, . Найдем условные вероятности наступления события при осуществлении каждой из гипотез. Вероятность того, что взятая наугад деталь окажется первого сорта, при условии, что она изготовлена на первом станке, равна , соответственно другие условные вероятности равны и .

По формуле полной вероятности находим:

Рассмотрим возможность вычисления вероятности, используя результат проведенного опыта. Пусть условия испытания содержат некоторый неизвестный элемент, относительного которого может быть сделано различных гипотез: , образующих полную группу событий. Их вероятности известны , известны и их условные вероятности . Используя результаты опыта, можно вычислить другую условную вероятность по формуле Бейеса.

Теорема 7.5. (Теорема Бейеса). Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события:

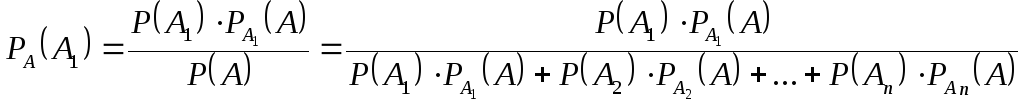(7.11)

Теорема Бейеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие .

Изменим условие последней задачи.

Пример 7.17. На склад поступили детали с трёх станков. На первом станке изготовлено 50% деталей от их общего количества, на втором – 30% и на третьем – 20%,причём на первом станке было изготовлено 85% деталей первого сорта, на втором – 80% и на третьем – 75%. Взятая деталь стандартная. Какова вероятность того, что она изготовлена на первом станке?

Решение:

Пусть событие состоит в том, что взятая наугад деталь окажется стандартной. Согласно формуле Бейеса:

3. Повторные независимые испытания

Практические задачи, связанные с оценкой вероятности наступления события в результате нескольких равноценных попыток могут анализироваться с применением формулы Бернулли или (при большом количестве таких попыток) с применением приближенной формулы Пуассона.

Схема Бернулли состоит в следующем: производится последовательность испытаний, в каждом из которых вероятность наступления определенного события одна и та же и равна . Испытания предполагаются независимыми (т.е. считается, что вероятность появления события в каждом из испытаний не зависит от того, появилось или не появилось это событие в других испытаниях). Наступление события обычно называют успехом, а не наступление – неудачей. Обозначим вероятность неудачи .

Вероятность того, что в независимых испытаниях успех наступит ровно раз, выражается формулой Бернулли:

(7.12)

Вероятность при данном сначала увеличивается при увеличении от 0 до некоторого значения , а затем уменьшается при изменении от до . Поэтому , называют наивероятнейшим числом наступлений успеха в опытах. Это число , заключено между числами:

(7.13)

Если число – целое число, то наивероятнейших чисел два: и .

Пример 7.5. Определить вероятность того, что в семье, состоящей из пяти детей, будет 3 мальчика и 2 девочки. Рождение девочки и мальчика считать равновероятным.

Решение:

Будем считать, что событие состоит в появлении мальчика. Поскольку вероятность появления мальчика и девочки равны, то , . Согласно условию: , . Найдем число сочетаний

Согласно формуле Бернулли, искомая вероятность равна:

При решении примеров, рассмотренных ранее, вычисление вероятностей не вызывало затруднений, так как число испытаний n было невелико. Однако, если число испытаний достаточно велико, то использование формулы Бернулли нецелесообразно в силу необходимости выполнения громоздких вычислений. Например, требуется вычислить P₃₂₀(285) при p=0,89.

^.

Получить здесь более или менее точный результат практически невозможно. Локальная теорема Лапласа, представляет собой асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно m раз в n испытаниях, если число испытаний достаточно велико.

(7.14)

(7.15)

— функция Гаусса;

(7.16)

Для упрощения расчетов по формуле (7.14) составлены таблицы, в которых помещены значения функции , соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция четная, то есть . Такие таблицы обычно приводятся в различных учебника, справочниках по теории вероятностей и математической статистике.

Пример 7.6. Два спортсмена играют в настольный теннис. Вероятность выигрыша первого спортсмена равна 5/9. Какова вероятность того, что он выиграет две партии из пяти?

Решение:

, , , .

.

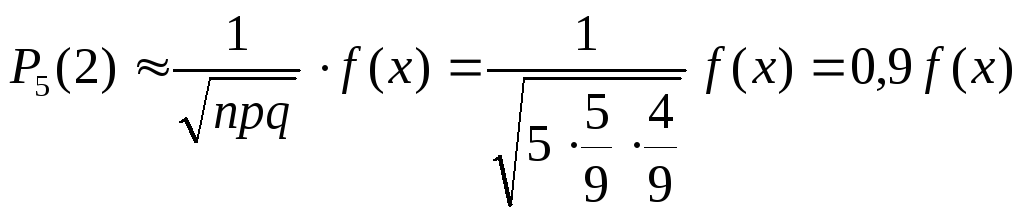Найдем значение аргумента .

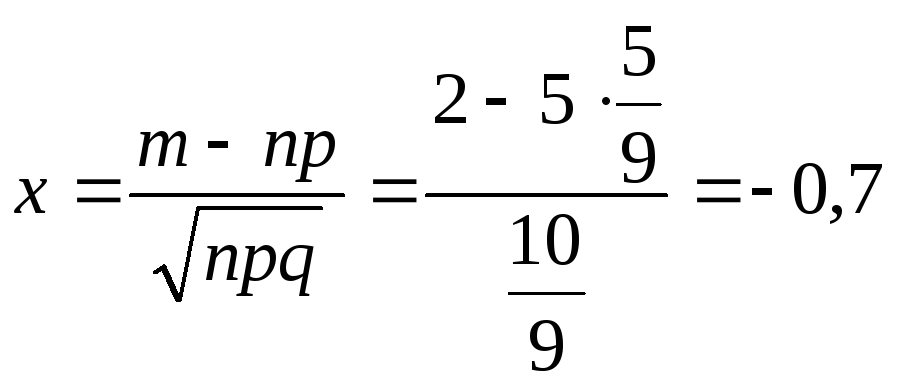По таблицам находим Искомая вероятность, равна

.

Проверим полученный результат, воспользовавшись формулой Бернулли. Имеем:

.

Расхождение ответов объясняется тем, что формула (7.14) дает хорошее приближение при больших значениях n, а в данном случае n = 5. Формула (7.14) позволяет получить более близкие к точному значению результаты, чем больше значение и чем ближе значения p и q к 0,5.

Если вероятность события p (или q) в отдельном испытании близка к нулю, то даже при большом числе испытаний , но небольшой величине произведения (меньше 10) вероятности , полученные по формуле (7.14) недостаточно близки к их истинным значениям. В таких случаях применяют другую асимптотическую формулу – формулу Пуассона, справедливость которой доказывается следующей теоремой.

Теорема. 7.6. Если вероятность p наступления события в каждом испытании постоянна, но близка к нулю, число независимых испытаний достаточно велико, а произведение (при этом ), то вероятность того, что в n независимых испытаниях событие наступит раз, приближенно равна:

(7.17)

(формула Пуассона).