2. Диференційні рівняння однорідної лінії

Напруга і струм в лінії є функціями двох незалежних перемінних: просторової координати х, що визначає місце спостереження, та часу t, який визначає момент спостереження. Нашою задачею є знаходження просторово-тимчасового розподілу величини струму у лінії i(x, t) та напруги поміж дротами u(х, t).

Складемо диференційні рівняння, яким задовольняють напруга і струм у будь-якому перетині двохпровідної лінії.

Домовимося називати верхній дріт (рис.3) двохпровідної лінії прямим, а нижній - зворотним. Позитивні напрями струму та напруги оберемо, як показано на рис 3.

Хай відомі первинні параметри однорідної лінії: r₀ - опір прямого та зворотного дротів, L₀ - індуктивність петлі, що утворюється прямим та зворотним дротами, g₀ - провідність (відплив) поміж дротами. С₀ - ємність між дротами.

Довгу лінію можна уявити у вигляді множини сполучених у ланцюжок нескінченно малих елементів довжиною dx, кожний з яких має опір r₀dx та індуктивність L₀dx, провідність g₀dx і ємність C₀dx (рис.3). Опір r₀dx та індуктивність L₀dx будемо рахувати включеними у один дріт.

Позначимо через х відстань від початку лінії до поточного елемента її довжини. Миттєві значення напруги та струму на початку обраного елемента лінії dx позначимо через u та i, а на початку наступного - через та

Рис. 3

Для елемента лінії довжиною dx на підставі законів Кірхгофа

Наводячи подібні члени і нехтуючи величиною другого порядку малості та скорочуючи на dx, одержуємо диференційні рівняння

(1.1)

Ці рівняння називають телеграфними рівняннями. Вони можуть бути вирішені однозначно при використанні початкових й граничних умов. Початковими умовами будуть значення напруги та струму на початку або в кінці лінії в момент часу, прийнятий за нуль. Граничні умови визначаються зв'язками між напругою та струмом на початку або в кінці лінії, які залежать від заданого режиму роботи лінії.

Розв'язання зазначених вище рівнянь дає функціональні залежності напруги та струму у лінії від перемінних х та t.

3. Періодичний режим в однорідній лінії

Розглянемо періодичний режим в довгій лінії при синусоїдальній напрузі джерела живлення. Позначимо комплексні діючі значення напруги та струму на відстані х від початку лінії через та.

Застосовуючи комплексну форму запису, одержуємо на підставі (1.1):

(1.2)

Де Z₀ = r₀+jL₀ - комплексний опір та Y₀ = g₀+jC₀ - комплексна провідність лінії одиничної довжини.

Зважаючи на те, що комплексні величини та не залежать від t і є лише функціями х, при переході від рівнянь (1.1) до (1.2) часткові похідні по х замінені звичайними.

Продифференцюємо рівняння (1.2):

(1.3)

і замінимо та згідно (1.2). В результаті отримаємо

(1.4)

Де

Позначимо квадратний корінь з комплексного множника при чи через

(1.5)

Назвемо цю величину коефіцієнтом розповсюдження. Рівняння (1.3) та (1.4) записуються у виді

(1.6)

Маємо однакові однорідні лінійні диференційні рівняння другого порядку. Рішення лінійного диференційного рівняння другого порядку з постійними коефіцієнтами має вигляд

(1.7)

Де - комплексні постійні інтегрування.

Струм знаходиться підстановкою (1.7) у перше рівняння (1.2)

чи

(1.8)

Де

(1.9)

називається хвильовим опором лінії.

Хвильовий опір і коефіцієнт розповсюдження називаються вторинними параметрами однорідної лінії.

Миттєве значення напруги у точці x рівно явної частини виразу .

(1.10)

Тут₁ та ₂ - аргументи комплексних величини та .

Миттєве значення струму має вигляд

(1.11)

де .

Таким чином, миттєві значення напруги і стуму у будь-якій точці лінії складаються з двох функцій. Кожен з додатків можна розглядати як біжучу хвилю, яка рухається в напрямку зростання чи зменшення координати х та згасаючу в напрямку руху. Кожен з додатків в будь-якій фіксованій точці х = x₁ подає собою гармонійну функцію з постійною амплітудою. Якщо ж лічити момент часу t фіксованим і розглядати зміну миттєвої напруги вздовж лінії (т. ч. в залежності від х), то отримаємо згасаючу гармонійну хвилю напруги (струму), амплітуда якої зменшується із зростанням х, т. ч. по мірі відходу від початку лінії до кінця.

Величина , що характеризує зміну амплітуди хвилі на одиницю довжини лінії, називається коефіцієнтом згасання, а величина , що характеризує зміну фази на одиницю довжини лінії, називається коефіцієнтом фази.

Згасання амплітуди хвилі вздовж лінії обумовлюється втратами в лінії, а зміна фази кінцевою швидкістю розповсюдження електромагнітних коливань.

Обидва коефіцієнта  та  входять в комплексний параметр =+j, який характеризує розповсюдження хвилі напруги та струму по лінії.

Основними характеристиками біжучої хвилі є фазова швидкість та довжина хвилі.

Фазовою швидкістю хвилі називається швидкість переміщення фази коливання, що впродовж часу t та по мірі збільшення відстані х, пройденого хвилею, залишається постійної, т. ч. , звідкіля слідує, що і

Аналогічне дослідження другого додатку правої частини рівності (1.10) дало би для фазової швидкості таке ж значення, але із зворотним знаком. Звідси укладаємо, що ці додатки можуть розглядатися як хвилі, які рухаються у протилежних напрямках.

Довжиною хвилі  називається відстань між найближчими двома точками, взятих в напрямі розповсюдження хвилі, фази коливання у яких розрізнюються на . Отже, для першого додатку рівності (1.10) отримаємо , звідки і , т. ч. за час, рівний періоду, хвиля пробігає відстань, рівну довжині хвилі. Одержана формула виражає залежність, існуючу між довжиною хвилі і коефіцієнтом фази лінії.

Хвилю, яка рухається від початку лінії, називають прямою, а яка рухається від кінця лінії - оберненою (зустрічною).

Згасаюча пряма хвиля представлена на рис.4. Для її зображення будують обвідні і вписують хвилю в область, обмежену обвідними.

Рис. 4

Оберемо позитивні напрями напруг та струмів окремих хвиль. Так як обидва додатки в правій частині рівняння (1.7), що визначають напругу U, входять із позитивними знаками, то обираємо позитивними напрямами напруг прямої і оберненої хвиль напрями, які співпадають із позитивним напрямом напруги , т. ч. від прямого дроту лінії до зворотного.

Для струму існують дві можливості. Можна залишити обидва додатки в правій частині рівності (1.8) із різними знаками або ж поставити між додатками знак плюс, а мінус включити в склад другого додатка. Будемо визначати струм , як різницю струмів прямої та оберненої хвиль, т. ч. позитивний напрямок струму прямої хвилі оберемо співпадаю чим із позитивним напрямком струму , а позитивний напрямок струму оберненої хвилі - протилежним позитивному напрямку струму .

У відповідності із цим можна записати

;

,

де;.

Напруга та струм прямої і відповідно оберненої хвиль зв'язані законом Ома:

.

Це співвідношення пояснює зміст назви - хвильовий опір.

Запроваджені поняття про пряму та обернену хвилі у лініях при синусоїдному встановленому режимі полегшують уявлення та аналіз процесів. Фізично існують у лінії тільки результуючі струм та напруга , і розкладання їх на прямі та обернені хвилі слідує рахувати лише зручним заходом.

Криві розподілу миттєвих значень напруг та струмів також мають хвилеподібний характер (рис.5). Вони показують, що в кожний момент часу результуючі струми та напруги, а також струми та напруги прямої та оберненої хвиль, у різних точках лінії можуть розрізнятися не тільки по значенню, але й по знаку.

Рис. 5

Постійні інтегрування та знаходяться у прямій залежності від напруги та струму на початку лінії (граничні умови), якщо вони задані. При x=0

;

,

звідкіля;.

Введемо поняття коефіцієнту відбивання хвилі на початку лінії:

, (1.12)

Де - вхідний опір лінії.

Підстановка виразу для та до (1.7) та (1.8) з урахуванням (1.12) дає:

(1.13)

Якщо задані граничні умови на кінці лінії, то краще відраховувати відстань від кінця, прийнявши координату х'.

Замінюючи у рівняннях (1.7) та (1.8) х на (l - х)' й використовуючи задані граничні умови; одержуємо для та , наступні вирази:

;.

Підставив їх до (1.7) та (1.8), отримаємо остаточні вирази для та :

(1.14)

Де аналогічно попередньому n₂ - коефіцієнт відбивання у кінці лінії:

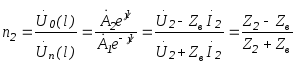; (1.15)

- вихідний опір на кінці лінії або у випадку приймача вхідний опір його.

Система рівнянь (1.14) може бути переписана у наступному виді.

(1.16)

Рівняння (1.14) та (1.16) подають собою рівняння лінії у показовій (або хвильовій) формі при відліку відстані від кінця лінії. Вони перетворюються за допомогою гіперболічних функцій:

(1.17)

Поклавши у цих рівняннях х' = l, отримаємо рівняння лінії у гіперболічній формі, що виражають напругу та струм на початку через напругу та струм у кінці лінії:

(1.18)

Показова і гіперболічна форми запису рівнянні лінії (1.14) та (1.17) взаємно доповнюють друг друга й застосовуються в залежності від умов задачі.

Холостий хід, коротке замикання лінії

Розглянемо холостий хід лінії. Якщо в режимі навантаження напруга та струм у кінці лінії були та , то після відключення навантаження напруга на кінці її при незмінній напрузі на початку лінії зміниться. Змінивши напругу на початку лінії так, щоб напруга у кінці лінії залишилася рівною , з (1.18) при холостому ході отримаємо

Якщо тепер, не змінюючи напруги на початку лінії, замкнути її на кінці, струм на кінці уже не буде рівний і у ряді випадків зросте. Змінивши напругу на початку лінії так, щоб струм в кінці замкненої лінії став рівним , з (1.18) отримаємо

На підставі цих співвідношень можна написати

Отримані формули показують, що дійсні струм та напруга у будь-якій точці лінії можуть бути розкладені на складові холостого ходу та короткого замикання, чим інколи зручно користуватися при розрахунках. Наприклад, при розрахунку розподілу струму та напруги вздовж навантаженої лінії з втратами можна спочатку знайти складові напруги та струму при холостому ході й короткому замиканні в окремості, а після цього, геометричні склавши їх, отримати дійсні струми та напруги.