3. Приведение квадратичной формы к каноническому виду по методу собственных значений.

Определение 1. Самосопряженный линейный оператор A в евклидовом пространстве E_n называется присоединенным к квадратичной форме f(x), если

f(x) = (x, Ax). (1)

Теорема 1. Если квадратичная форма имеет присоединенный линейный оператор, то в любом ортонормированном базисе его матрица равна матрице квадратичной формы.

Доказательство. В ортонормированном базисе, соотношение (1) запишется в виде X ^t B X = X ^tA X, где A - матрица оператора A, B - матрица квадратичной формы, X - координатный столбец вектора x. Это равенство можно записать в виде

X ^t (B-A) X = 0. (2)

Так как матрицы B, A - симметрические, то симметрическая матрица B - A. Рассмотрим квадратичную форму с матрицей B - A. Равенство (2) означает, что значение этой квадратичной формы равно нулю для каждого вектора x. Тогда форма канонического вида для этой формы нулевая, ранг ее равен нулю , и все ее коэффициенты равны нулю. Отсюда B = A. 

Теорема 2. Каждая квадратичная форма имеет присоединенный линейный оператор, и только один.

Доказательство. Выберем в E_n какой-нибудь ортонормированный базис пространства E_n, и рассмотрим в E_n тот линейный оператор, который имеет матрицу, равную матрице B квадратичной формы f(x). Найденный линейный оператор A самосопряженный, так как в ортонормированном базисе имеет симметрическую матрицу. Так как из B = A следует X ^t B X = X ^tA X, и f(x) = (x, Ax).

Докажем, что квадратичная форма имеет только один присоединенный линейный оператор. Допустим, что квадратичная форма f(x) имеет два присоединенных линейных оператора A, B. По теореме 1 в ортонормированном базисе его матрица равна матрице квадратичной формы f(x). Тогда матрицы операторов A, B в одном и том же базисе равны и операторы A, B совпадают. 

Теорема 3. В евклидовом пространстве для каждой квадратичной формы существует ортонормированный базис, в котором квадратичная форма имеет канонический вид.

Доказательство. Рассмотрим линейный оператор A, присоединенный к квадратичной форме f(x). По теореме 2.5 предыдущей лекции, существует базис евклидова пространства, состоящий из собственных векторов линейного оператора A. Матрица линейного оператора в этом базисе диагональная. Тогда и матрица квадратичной формы диагональная, а квадратичная форма имеет канонический вид.

Следствие. Для любой квадратичной формы f(x) существует такое ортогональное преобразование переменных, которое приводит данную квадратичную форму к каноническому виду.

Доказательство. Существование преобразования следует из теоремы 2. То что преобразование ортогональное следует из того, что матрица перехода от одного ортонормированного базиса к другому ортогональная.

Пример 1. Привести квадратичную форму к каноническому виду ортогональными преобразованиями и найти эти преобразования

Решение. Рассмотрим присоединенный к квадратичной форме f(x) линейный оператор A евклидовом пространстве Е₃, который имеет, имеет в ортонормированном базисе e₁, e₂, e₃ матрицу

.

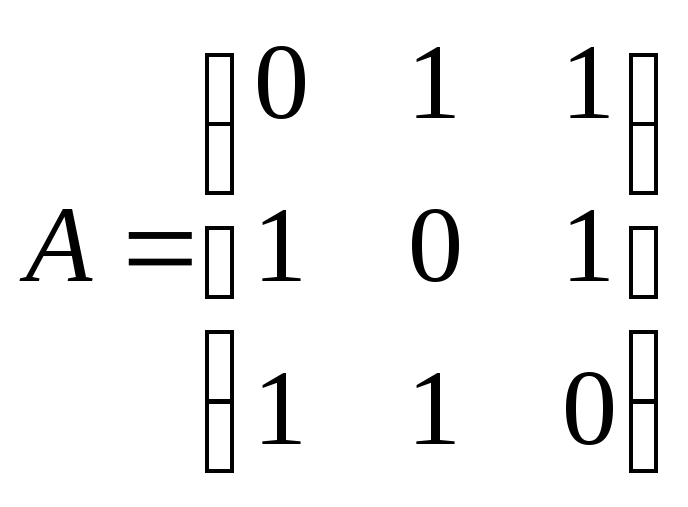Составить характеристическое уравнение линейного оператора A - .E = 0.

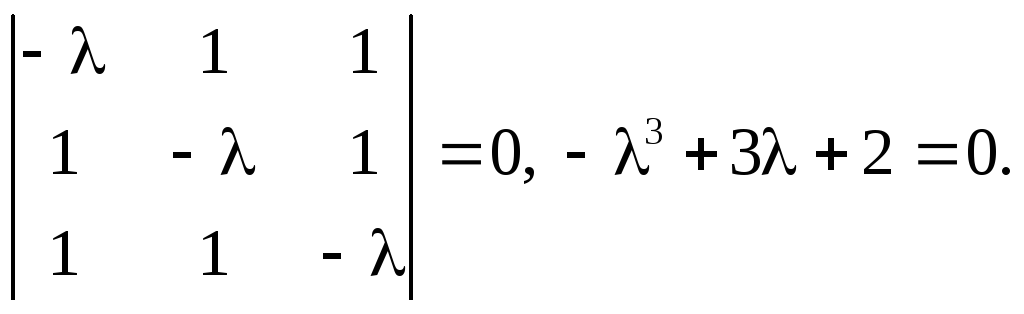
Найдем все корни характеристического уравнения: ₁=2, ₂ = ₃ = -1. Тогда матрица линейного оператора в ортонормированном базисе, составленном из собственных векторов имеет вид

.

Составим квадратичную форму канонического вида

Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A - .E)X=0.

Пусть ₁=2. Матричное уравнение (A - ₁E)X=0 принимает вид:

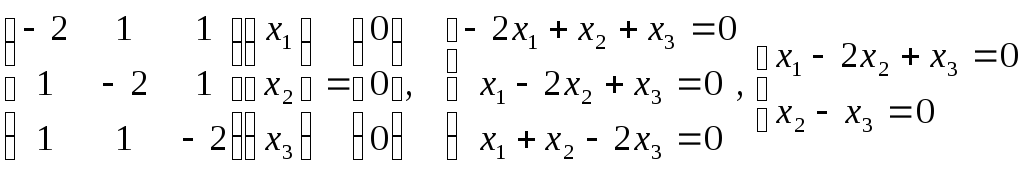
Решая систему, находим решение x = c(1,1,1), cR/{0}.

Пусть ₂ = ₃ = -1. Матричное уравнение (A - ₁E)X=0 принимает вид:

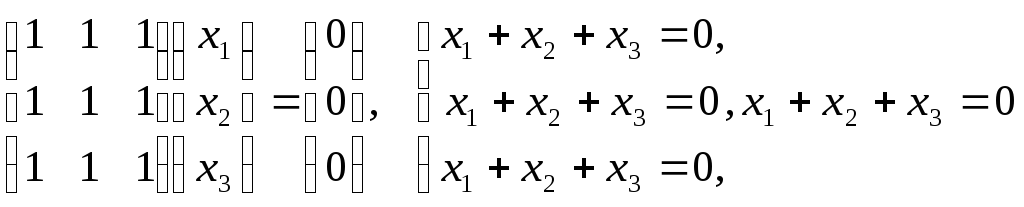
Решая систему, находим решение x = c₁(-1,1,0) + c₂(-1,0,1), cR.

Полученный базис a₁ = (1,1,1), a₂ = (-1,1,0), a₃ =(-1,0,1) ортонормируем.

b₁ = (1,1,1), b₂ = (-1,1,0), b₃ = a₃ + k b₂, , b₃ =(-1/2, 1, -1/2).

.

Ортогональное преобразование, переводящее квадратичную форму в форму канонического вида, имеет вид