4. Линейная алгебра и аналитическая геометрия

4.1. Матрицы

Прямоугольная таблица из чисел вида

,

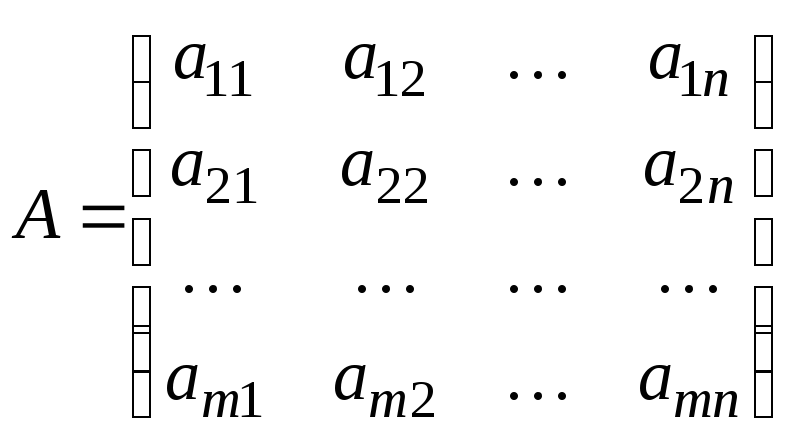состоящая из m строк и n столбцов, называется матрицей размеров m  n.

Матрица называется обратной к квадратной матрице А, если , где Е – единичная матрица. Для невырожденной матрицы , где – определитель матрицы А, существует единственная обратная матрица

,

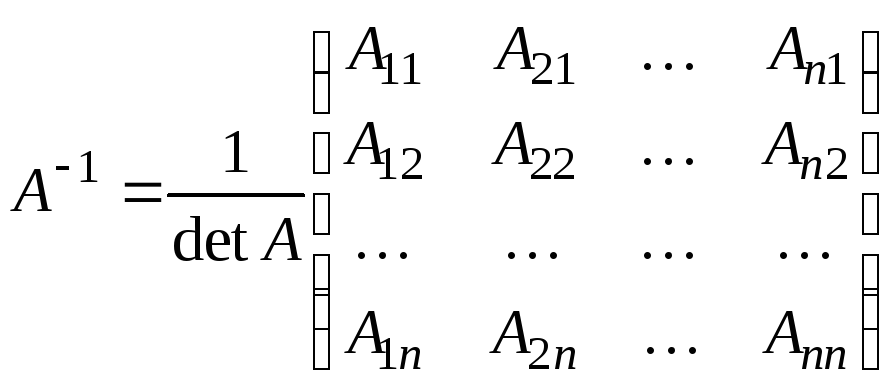где – алгебраические дополнения элементов матрицы А.

Если матрица А – вырожденная , то обратной к ней не существует.

Пример 4.1. Найти матрицу , обратную к матрице

.

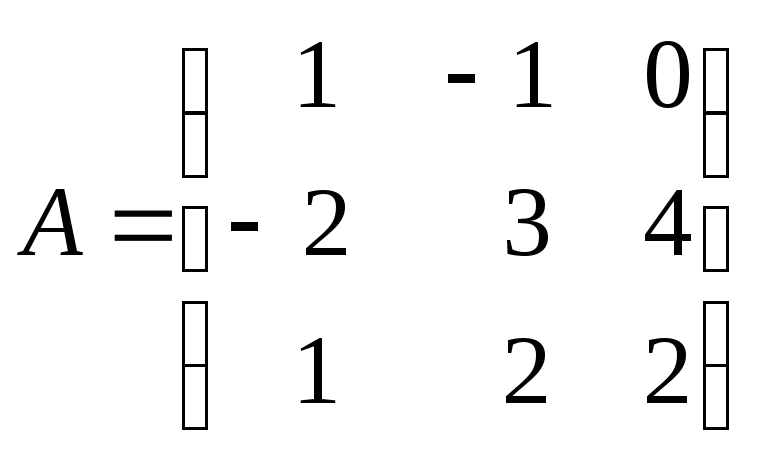Так как , то – невырожденная и существует. Найдем алгебраические дополнения элементов матрицы :

;

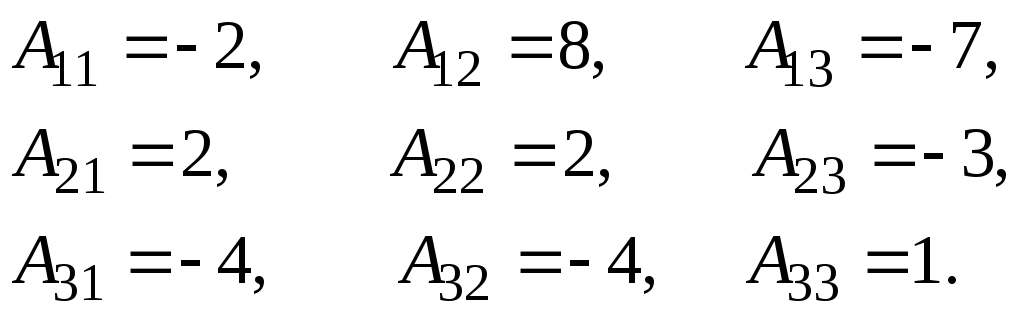
Следовательно,

.

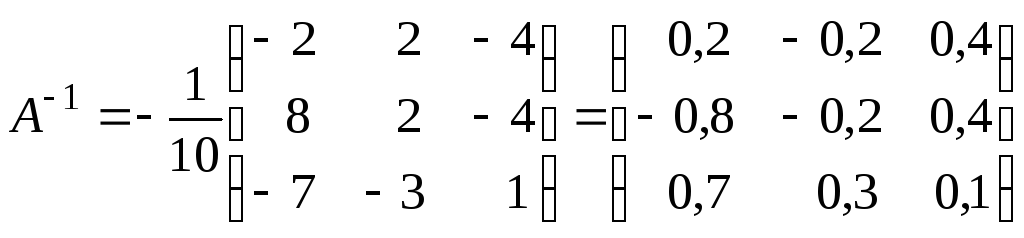4.2. Системы линейных уравнений. Матричный метод. Правило Крамера. Метод Гаусса

Пусть задана система n линейных уравнений с n неизвестными вида

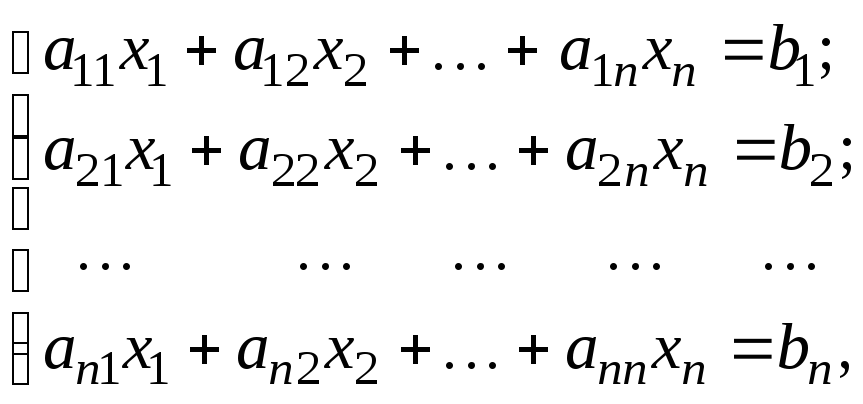(4.1)

или, в матричной форме

А Х = В,

где

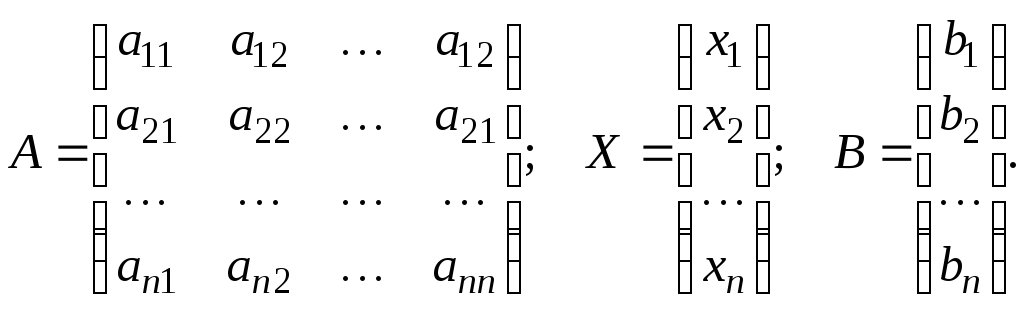
Рассмотрим некоторые методы решения системы (4.1).

Формулы Крамера. Если система (4.1) невырождена, то она имеет единственное решение, определяемое формулами Крамера:

где – определитель, получаемый из определителя заменой его i-го столбца на столбец В свободных членов.

Матричный метод.

Решение невырожденной системы (4.1) можно найти по формуле .

Метод последовательного исключения неизвестных (метод Гаусса).

С помощью элементарных преобразований над строками система m линейных уравнений с n неизвестными может быть приведена к виду

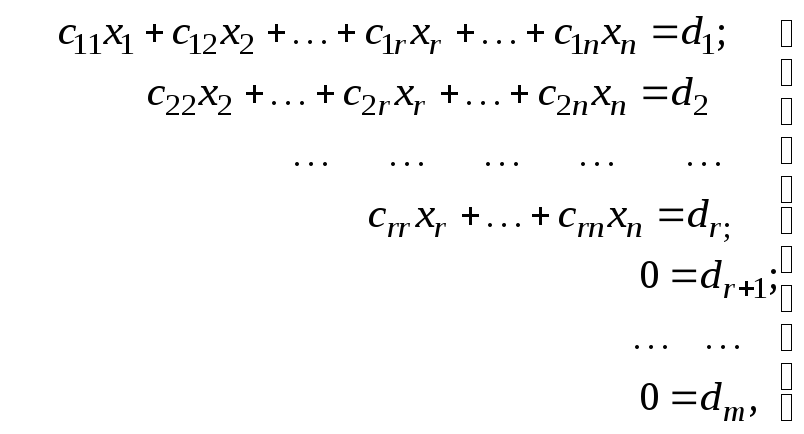, (4.2)

где

Система (4.2) эквивалентна исходной системе. Если хотя бы одно из чисел отлично от нуля, то система (4.2), а следовательно, и исходная система несовместны. Если же то система совместна и из уравнений (4.2) выражают последовательно неизвестные через .

Пример 4.2. Методом Гаусса решить систему

Решение. Расширенная матрица системы имеет вид

Производя элементарные преобразования над строками расширенной матрицы, получаем

где цифрами обозначены следующие операции:

– первую и вторую строки поменяли местами; – ко второй строке прибавили первую, умноженную на (–2); к третьей прибавили первую, умноженную на (–3); – к третьей строке прибавили вторую, умноженную на (–1).

Этой матрице соответствует система

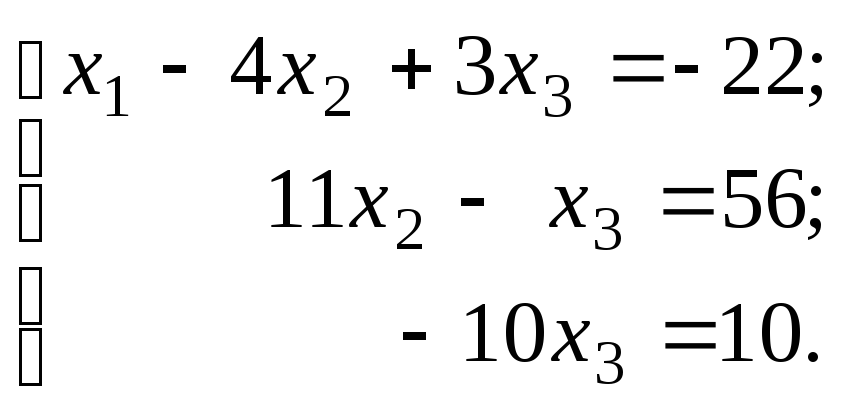
Отсюда последовательно находим

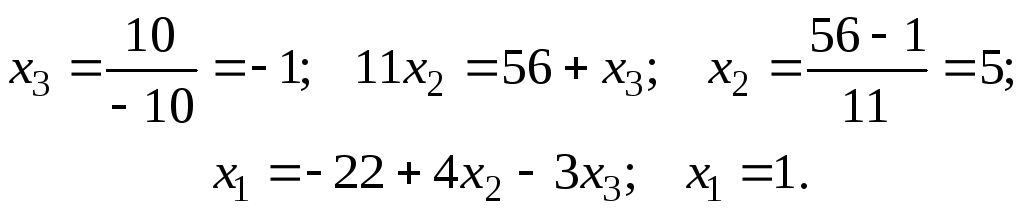
Ответ:

Пример 4.3. Решить систему уравнений

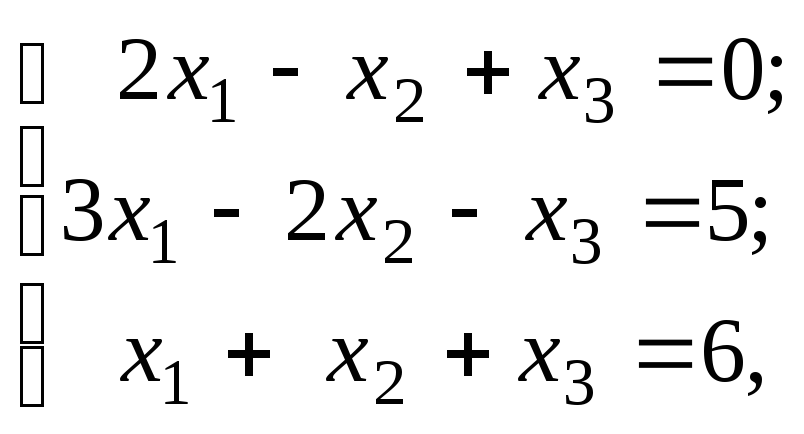
используя формулы Крамера.

Решение. Так как определитель данной системы

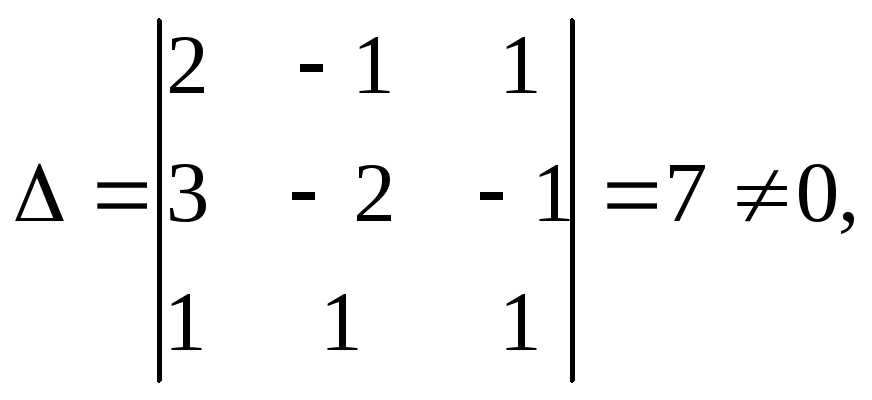
то матрица А невырождена и система имеет единственное решение.

Находим определители

По формулам Крамера находим решение системы:

4.3. Скалярное произведение векторов

Скалярным произведением векторов и называется число, обозначаемое или и равное где – угол между и .

Свойства скалярного произведения:

1. 2.

3. 4.

Свойство 4 выражает условие ортогональности векторов.

Если векторы и представлены своими координатами в ортонормированном базисе , то скалярное про-изведение равно

Из этой формулы и определения скалярного произведения следует:

Учитывая, что где – проекция вектора на вектор , а скалярное произведение векторов можно записать в виде

Пример 4.4. Даны векторы Найти .

Решение.

Поскольку

а векторы заданы координатами в ортонормированном базисе, то

Поэтому

Механический смысл скалярного произведения: работа А, про-изводимая силой точка приложения которой перемещается из точки в точку вычисляется по формуле