1.2. Матрицы Основные определения

Матрицей размерности m называется прямоугольная таблица элементов, расположенных в m строках и n столбцах:

.

Элементами матрицы могут быть необязательно числа. Однако в математике нас интересуют, как правило, числовые матрицы.

Если m=1, то имеем матрицу-строку

.

Если n=1, то имеем матрицу-столбец

.

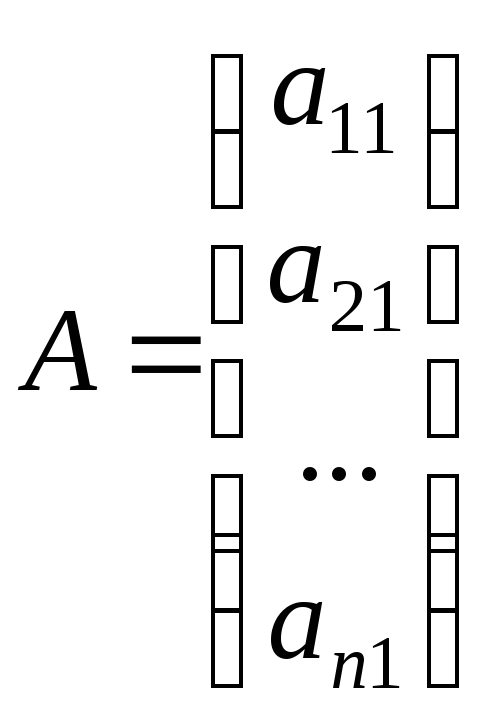Если n=т=n, то имеем квадратную матрицу n-го порядка

.

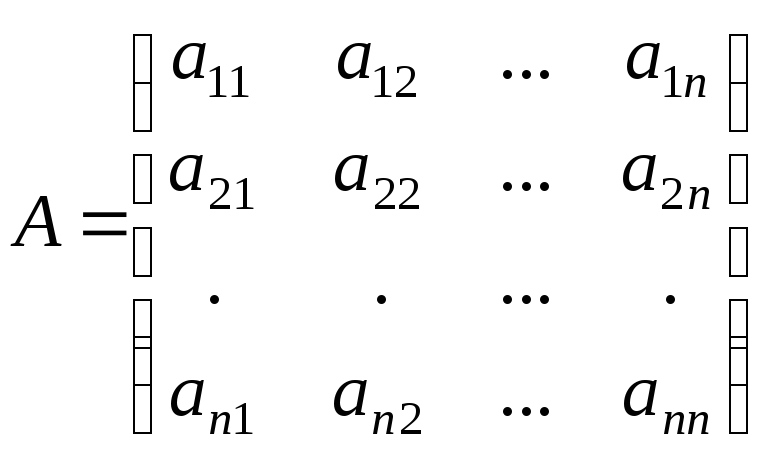В квадратной матрице различают элементы , , ..., , стоящие на главной диагонали матрицы и элементы , , ..., , стоящие на побочной диагонали.

Если в квадратной матрице все элементы, кроме элементов стоящих на главной диагонали, равны нулю, то матрица называется диагональной

.

Если элементы диагональной матрицы, стоящие на главной диагонали, равны единицам, то матрица называется единичной матрицей соответствующего порядка и обозначается через Е:

.

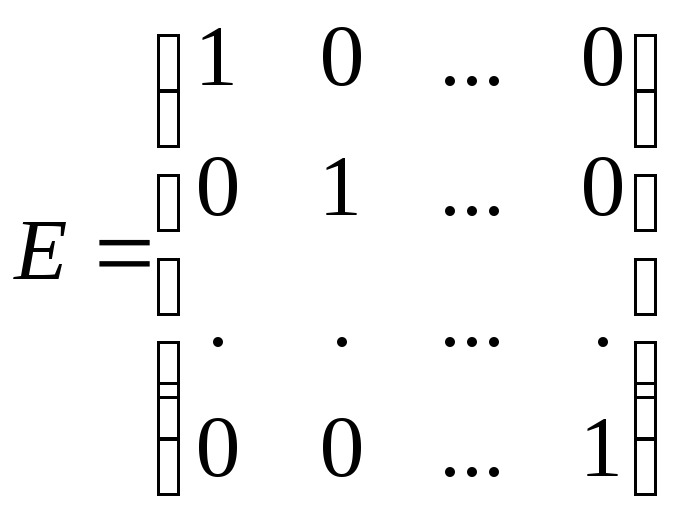Две матрицы равны тогда и только тогда, когда они имеют одинаковую размерность и когда в одинаковых ячейках (на одинаковых местах) матриц стоят одинаковые элементы.

Действия с матрицами

Умножение матрицы на число. При умножении матрицы на число, все элементы матрицы множатся на это число

.

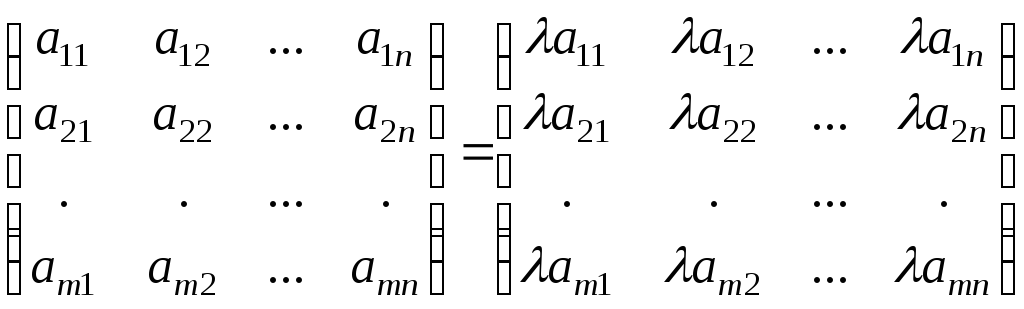Таким образом, сомножитель общий для всех элементов матрицы можно выносить за знак матрицы.

Сложение матриц. Складываться могут лишь матрицы одинаковой размерности. При сложении двух матриц одинаковой размерности, складываются их соответствующие элементы

.

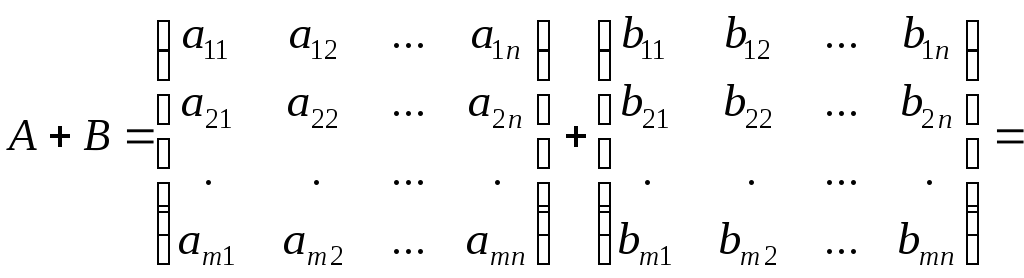
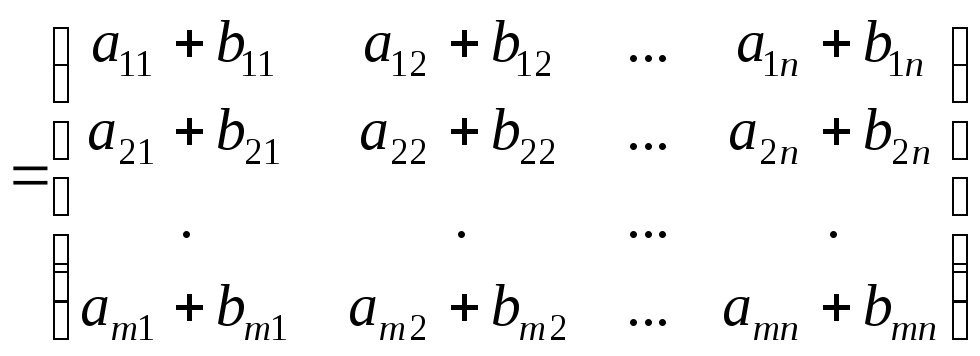При вычитании двух матриц одинаковой размерности, из элементов матрицы-уменьшаемого вычитаются соответствующие элементы матрицы-вычитаемого.

Перемножение матриц. Пусть имеем две матрицы A - первая матрица-сомножитель (матрица-множимое) и B - вторая матрица-сомножитель (матрица-множитель). Операция умножения матриц имеет смысл только тогда, когда количество столбцов матрицы-множимого (матрицы А) равно количеству строк матрицы-множителя (матрицы B). В результате умножения двух матриц получаем новую матрицу С, элемент которой (элемент, стоящий в i – той строке и в j–том столбце матрицы-произведения) получается как результат суммирования произведений элементов i–той строки матрицы А на соответствующие элементы j–того столбца матрицы В, например,

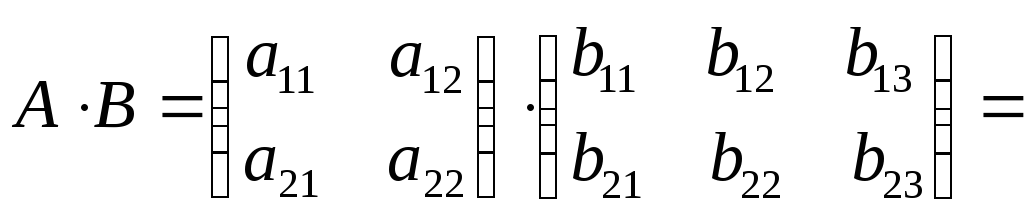
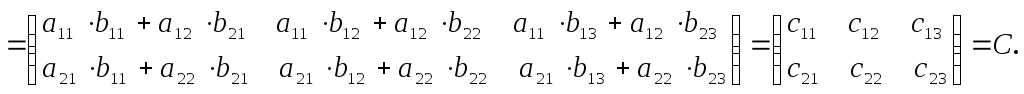
Таким образом, например, . Матрица А имеет два столбца, матрица В имеет две строки и поэтому их перемножение возможно. Матрица-произведение С содержит столько строк, сколько их имеет матрица-множимое А и столько столбцов сколько их имеет матрица множитель В.

П р и м е р 1.

.

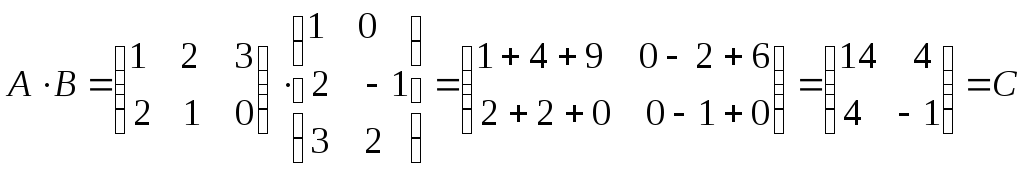П р и м е р 2.

.

П р и м е р 3.

.

Обращение матриц. Квадратной матрице , можно поставить в соответствие ее определитель. Так, например, если матрица имеет вид

,

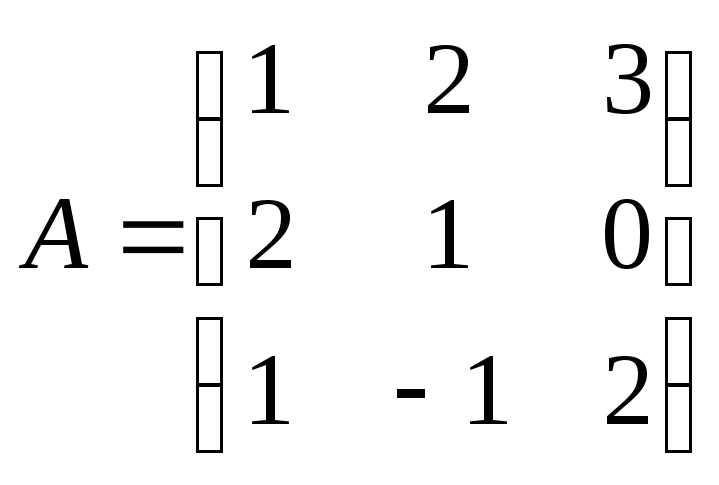то соответствующий ей определитель (детерминант) будет

.

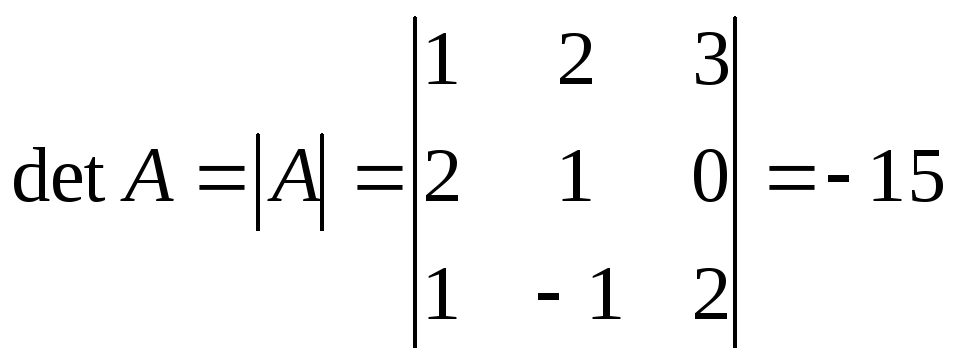В случае, если , говорят, что матрица А невырожденная или неособенная, если , то А – вырожденная или особенная матрица.

Квадратная матрица называется обратной по отношению к квадратной матрице А, если их произведение дает единичную матрицу соответствующего порядка .

Необходимое и достаточное условие существования обратной матрицы. Для того чтобы квадратная матрица А имела обратную матрицу необходимо и достаточно, чтобы матрица А была невырожденной.

Схема отыскания обратной матрицы

1. Для квадратной матрицы А находится . Убеждаемся, что последний определитель не равен нулю.

2. Строится матрица В – матрица алгебраических дополнений членов определителя .

3. Строится матрица - транспонированная матрица В .

4. Строится матрица .

П р и м е р . Найти обратную матрицу для матрицы

.

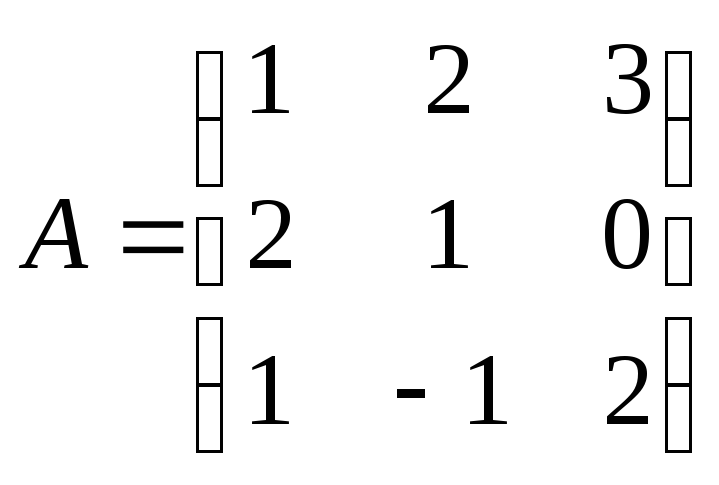Р е ш е н и е .

1. .

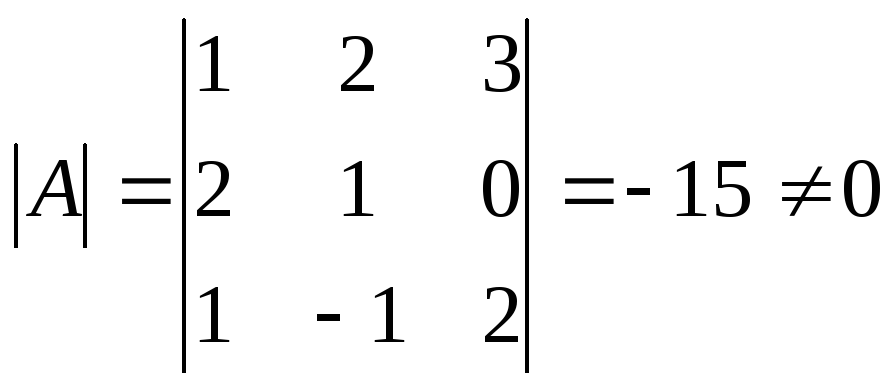2. Находим алгебраические дополнения элементов определителя :

, , ,

, , ,

, , .

Теперь

.

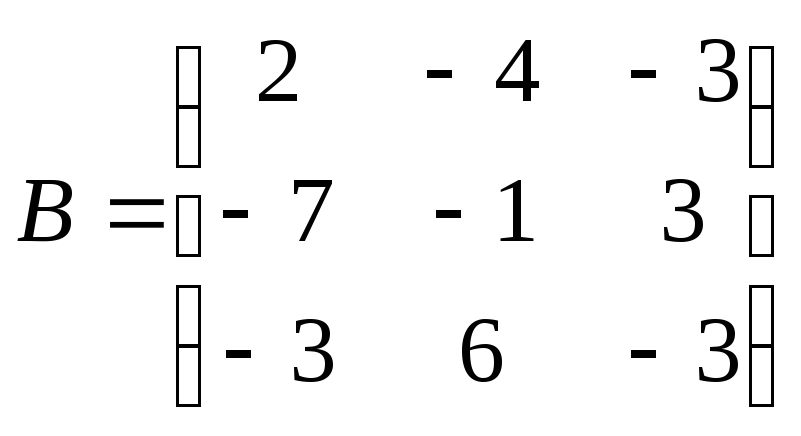3. .

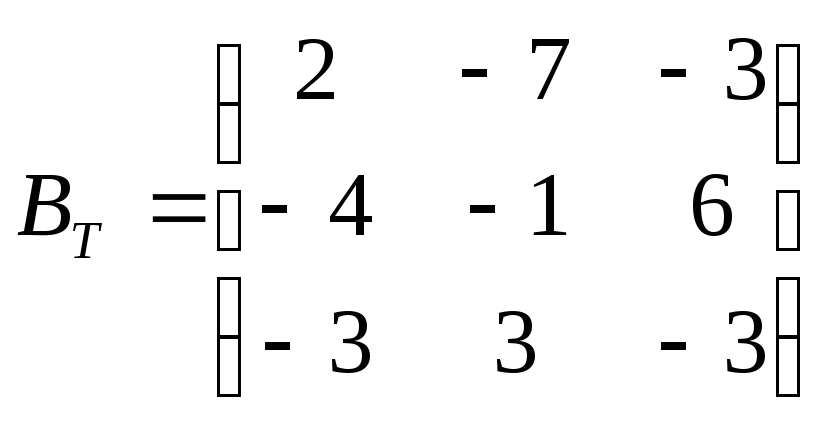4. .

П р о в е рк а :

.

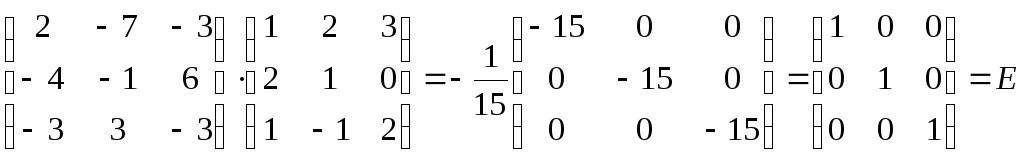В результате перемножения А на получили единичную матрицу, следовательно обратная матрица найдена верно.