
- •Передмова
- •Рекомендована література
- •Розділ 1. Матриці і системи лінійних алгебраїчних рівнянь (слар)
- •1.1. Матриці, визначники та їх властивості
- •1.2. Види матриць. Лінійні дії над матрицями
- •1.3. Множення матриць. Обернена матриця
- •1.4. Система п лінійних алгебраїчних рівнянь з п невідомими. Матричний спосіб розв’язання систем
- •1.5. Метод Гаусса розв’язання слар
- •Розділ 2. Вектори
- •2.1. Поняття вектора. Лінійні дії над векторами
- •Лінійні дії над векторами
- •2.2. Проекція вектора на вісь
- •2.3. Декартові координати
- •2.4. Приклади геометричних застосувань декартових координат
- •2.5. Скалярний добуток векторів
- •2.6. Геометричні застосування скалярного добутку
- •2.7. Векторний добуток векторів
- •2.8. Мішаний добуток трьох векторів
Розділ 2. Вектори
2.1. Поняття вектора. Лінійні дії над векторами
В математиці, фізиці, інших науках розглядаються величини двох видів: скалярні і векторні.
Скалярною величиною або скаляром називається величина, яка повністю характеризується своїм числовим значенням у обраній системі одиниць (наприклад, температура, робота, густина, тощо).
Векторною величиною називається величина, яка крім числового значення визначається ще й своїм напрямом у просторі (наприклад, швидкість, сила і т.п.).
Векторну
величину можна зобразити напрямленим
прямолінійним відрізком, який називають
вектором;
довжина його дорівнює числовому значенню
векторної величини (у обраному масштабі),
а напрям такий, як у цієї величини.
Вектори позначають малими латинськими
буквами з рискою або стрілочкою над
ними, або ж надрукованими напівжирним
шрифтом (![]() ,
,![]() ,q).
Вектор може визначатися своєю початковою
і кінцевою точками; вектор, початком
якого є точка А,
а кінцем точка В,
позначається
,q).
Вектор може визначатися своєю початковою
і кінцевою точками; вектор, початком
якого є точка А,
а кінцем точка В,
позначається
![]() .
.
Числове
значення вектора, тобто довжина
відповідного напрямленого відрізка,
називається довжиною
або модулем
вектора і позначається
![]() або а
(без риски),
або а
(без риски),
![]() або АВ.
або АВ.
Вектор
нульової довжини називається нульовим
вектором
і позначається
![]() .
.
Вектори, паралельні одній прямій, називаються колінеарними; паралельні одній площині – компланарними.
Вектори рівні, якщо вони мають однакові напрями і рівні модулі, отже можуть бути одержані один з одного паралельним перенесенням, а положення їх точки прикладання (початку) не відіграє ролі. Вектори за останньою умовою називають вільними. Далі розглядаються тільки вільні вектори.
Два
вектори протилежні
один одному, якщо вони мають рівні модулі
і протилежні напрями. Вектор, протилежний
вектору
![]() ,
позначається –
,
позначається –![]() ,
протилежний вектору
,
протилежний вектору
![]() позначається
позначається
![]() = –
= –![]() .
.
Лінійні дії над векторами
Лінійними діями над векторами називаються додавання (і пов’язане з ним віднімання) векторів і множення вектора на число (скаляр).
Сумою
векторів
![]() і
і
![]() є вектор, який іде з початку вектора
є вектор, який іде з початку вектора
![]() в кінець вектора
в кінець вектора
![]() при умові, що вектор
при умові, що вектор
![]() відкладений від кінця вектора
відкладений від кінця вектора
![]() (рис 2.1). Це так зване „правило трикутника”.
(рис 2.1). Це так зване „правило трикутника”.
Іншим
способом побудови суми двох векторів
є так зване „правило паралелограма”:
якщо вектори
![]() і
і
![]() відкладені від спільного початку О
відкладені від спільного початку О
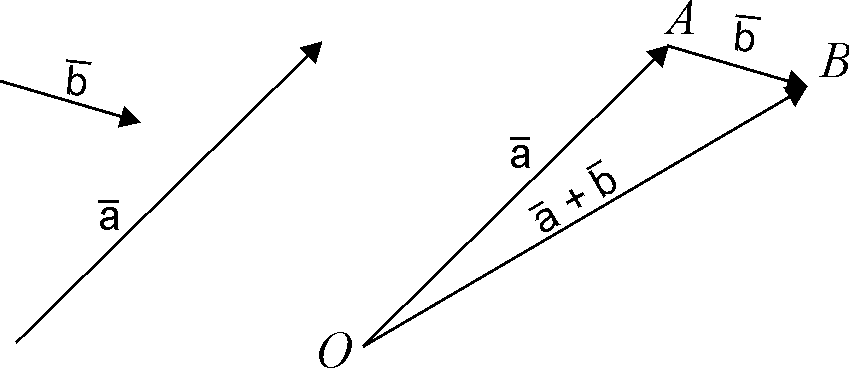
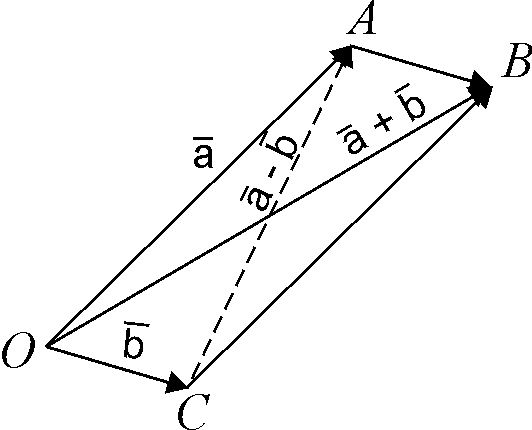
Рис. 2. 1 Рис. 2. 2
(рис.
2.2) і на них побудовано паралелограм, то
сума
![]() +
+
![]() є вектор
є вектор
![]() ,
який виходить з того ж початку і
суміщається з діагоналлю паралелограма.
Зауважимо, що обидва правила дають один
і той же результат. Справді, на рис. 2.2
маємо
,
який виходить з того ж початку і
суміщається з діагоналлю паралелограма.
Зауважимо, що обидва правила дають один
і той же результат. Справді, на рис. 2.2
маємо
![]() =
=
![]() ,
,
![]() =
=
![]() ,
отже
,
отже
![]() =
=
![]() +
+![]() =
=
![]() +
+
![]() за „правилом трикутника”, так само, як
і за „правилом паралелограма”.
за „правилом трикутника”, так само, як
і за „правилом паралелограма”.
„Правило трикутника” легко узагальнюється на випадок суми трьох або більше векторів: від кінця першого вектора відкладаємо другий, від кінця другого – третій і т.д. Сумою всіх цих векторів є вектор, який іде з початку першого вектора в кінець останнього (рис. 2.3). Це так зване „правило многокутника”.
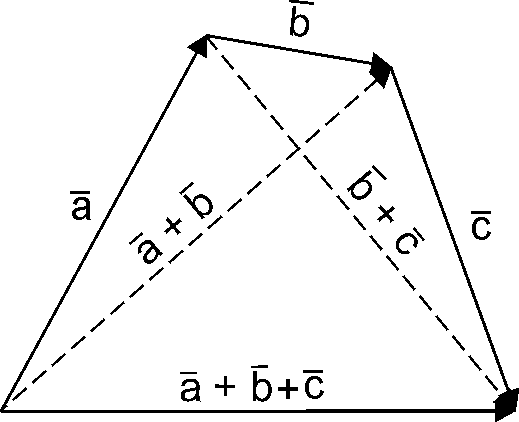
Рис. 2. 3
Дія додавання векторів:
-
комутативна, тобто
 +
+
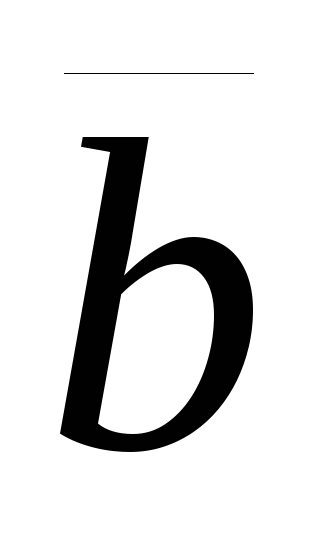 =
=
 +
+
 (див. рис. 2.2);
(див. рис. 2.2); -
асоціативна, тобто (
 +
+
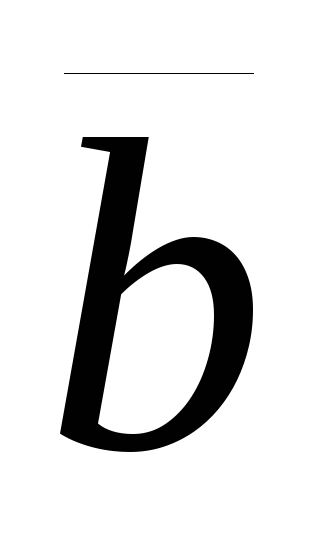 )
+
)
+
 =
=
 + (
+ (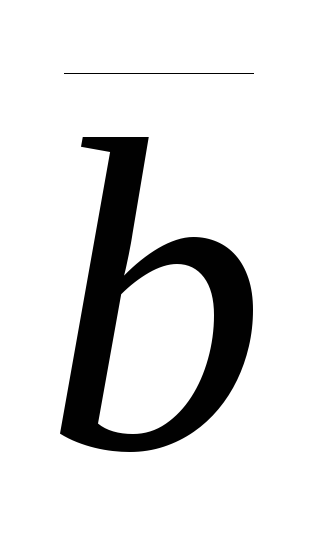 +
+
 )
(див. рис. 2.3), як і додавання чисел.
)
(див. рис. 2.3), як і додавання чисел.
Різницею
векторів
![]() –
–
![]() є сума вектора
є сума вектора
![]() і вектора, протилежного вектору
і вектора, протилежного вектору
![]() ,
тобто
,
тобто
![]() –
–
![]() =
=
![]() +(–
+(–![]() ).
).
На рис.
2.2 різниця
![]() –
–
![]() зображується другою діагоналлю
паралелограма ОАВС.
Справді
зображується другою діагоналлю
паралелограма ОАВС.
Справді
![]() +
+![]() =
=
![]() ,
тобто
,
тобто
![]() +
+![]() =
=
![]() ,
звідки
,
звідки
![]() =
=
![]() –
–
![]() .
.
Множення
вектора на число. Добутком вектора
![]() на
число λ
називається
вектор, який позначається
на
число λ
називається
вектор, який позначається
![]() або
або
![]() і
визначається такими умовами:
і
визначається такими умовами:
1)
![]() =
=![]() ;
;
2)
![]()
![]()
Інакше
кажучи: якщо λ
>
0, то
![]() – це вектор, який одержуємо із
– це вектор, який одержуємо із
![]() розтягом в λ
разів
без зміни напряму; якщо
λ
<
0, то потрібно розтягнути
розтягом в λ
разів
без зміни напряму; якщо
λ
<
0, то потрібно розтягнути
![]() в |λ|
разів
і, крім того, змінити напрям на протилежний.
в |λ|
разів
і, крім того, змінити напрям на протилежний.
Добуток вектора на число має такі властивості:
1) λ(μ![]() )=
(λμ)
)=
(λμ)![]() – асоціативність відносно числових
множників;
– асоціативність відносно числових
множників;
2) (λ
+ μ)![]() =
λ
=
λ![]() +
μ
+
μ![]() – дистрибутивність відносно числового
множника;
– дистрибутивність відносно числового
множника;
3) λ(![]() )=λ
)=λ![]() + λ
+ λ![]() –
дистрибутивність відносно векторного
множника;
–
дистрибутивність відносно векторного
множника;
4)
![]() =
=![]() для будь-якого числа
λ;
для будь-якого числа
λ;
5)
![]() =
=![]() для будь-якого вектора
для будь-якого вектора
![]() ;
;
6)
![]() =
=
![]() ;
;
![]() = –
= –![]() для будь-якого вектора
для будь-якого вектора
![]() .
.
Зазначимо,
що будь-який вектор
![]() можна подати у вигляді
можна подати у вигляді
![]() ,
де
,
де
![]() – орт
вектора
– орт
вектора
![]() ,
тобто вектор одиничної довжини, напрям
якого збігається з напрямом вектора
,
тобто вектор одиничної довжини, напрям
якого збігається з напрямом вектора
![]() .
.
Сформульовані властивості лінійних дій над векторами цілком аналогічні властивостям відповідних дій над числами, отже дозволяють при лінійних діях з векторами виконувати різні перетворення (розкриття дужок, винесення спільних множників, приведення подібних членів, тощо) так само, як із числами.
